Начнем с того, что выведем формулу Тейлора для многочлена

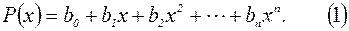
Зададим произвольное число а и в правой части (1) сделаем замену

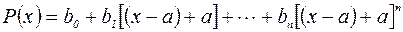
Теперь раскроем все квадратные скобки и приведем подобные члены с одинаковыми степенями (x–a). В результате получим

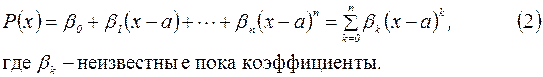
Равенство (2) называется разложением многочлена P (x) по степеням (x – a), а числа 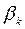называется коэффициентами этого разложения.

Будем последовательно дифференцировать равенство (2):

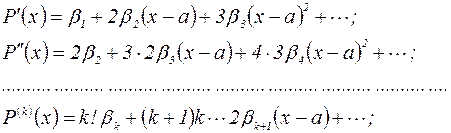
В последнем равенстве положим :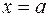

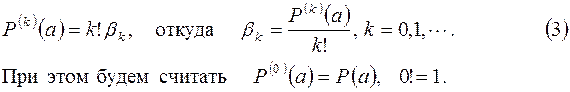
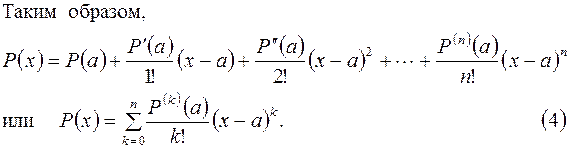
Формула (4) называется формулой Тейлора разложения многочлена степени n по степеням (x – a).

Если а=0, то формула называется формулой Маклорена:

Пример:

Бином Ньютона.

Пусть 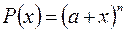, где а – произвольное число, а n – натуральное число.

k -я производная равна:

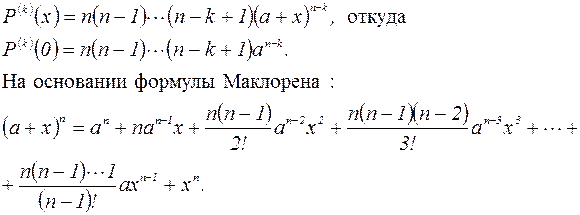
Это формула бинома Ньютона.

Если обозначить то формула записывается в виде .

Числа 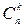называются биномиальными коэффициентами. Эти коэффициенты обладают следующими свойствами (доказать самостоятельно):

равенства можно легко вычислить 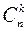для любых n и k, пользуясь только одним действием сложения.

Располагая коэффициенты 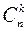при различных n в отдельные строки, получим так называемый треугольник Паскаля.

0 1

1 1 1

2 1 2 1

3 1 3 3 1

4 1 4 6 4 1

5 1 5 10 10 5 1

………………….

В строке, соответствующей конкретному значению n, находится (n+1) число:

Примеры.

.

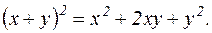
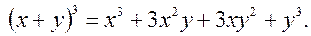
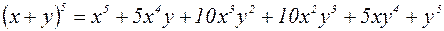Выведем теперь формулу Тейлора для произвольной функции. Пусть в окрестности точки а задана функция f (x), не являющаяся многочленом степени n–1, но имеющая в точке а производные до n -го порядка включительно.

Это многочлен степени (n–1). Он называется многочленом Тейлора степени (n–1) функции f (x) по степеням (x–a). Если бы исходная функция f (x) была многочленом степени (n–1), то выполнялось бы тождество f (x) =Q (x) для всех х из нашей окрестности.

Но в данном случае это тождество не имеет места, т.к. мы предположили, что f (x) не есть многочлен степени (n–1).

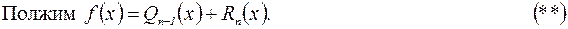
Здесь , где Q (x) определен формулой . Индекс (n–1) выписан для удобства, чтобы подчеркнуть, что Q (x) – многочлен степени (n–1).

Равенство называется формулой Тейлора функции f (x) в окрестности точки x=a, а 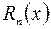– остаточным членом или n -м остатком формулы Тейлора.

Оказывается, остаточный член может быть записан в весьма изящной форме: либо в форме Лагранжа, либо в форме Коши.

Форма Лагранжа: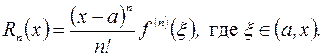

Точка зависит от x и n. Обычно точное значение неизвестно, но можно утверждать, что находится на интервале (a,x), при этом х можно считать как большим, чем а, так и меньшим, чем а.

Другой вид формы Лагранжа:

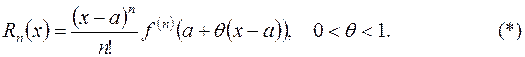
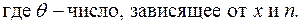
Остаточный член, записанный в форме (*) или (**), обычно используют для оценки точности приближенного вычисления функции f(x) в точке x, отличной от a.

Date: 2015-09-02; view: 545; Нарушение авторских прав