Отыскание точек возможного экстремума

Мы ввели понятия локального экстремума (локального максимума и локального минимума). Напомню: если функция определена в окрестности точки с и f (с) является наибольшим значением в этой окрестности, то точка с – точка локального максимума. Если же f (с) – наименьшее значение в указанной окрестности, то с – точка локального минимума. Если функция дифференцируема и имеет в точке с экстремум (max или min), то 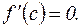Таким образом, для отыскания у дифференцируемой функции точек возможного экстремума следует найти все корни уравнения 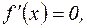т.е. найти все нули производной 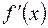. Эти точки называются точками возможного экстремума (стационарными точками).

Экстремум, однако, может быть, а может его и не оказаться. Достаточным же условием экстремума является смена знака у производной 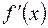в стационарной точке. При этом если 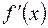при переходе через стационарную точку меняет знак с «–» на «+», то из области, где функция f (x) убывала, мы переходим к области, где она возрастает. В такой стационарной точке функция имеет минимум. Если же производная меняет знак с «+» на «–», то f (x) в такой стационарной точке имеет максимум.

Производная может не изменять знака при переходе через стационарную точку: в этом случае экстремума (максимума или минимума) нет.

Примеры.

1. Возьмем предыдущий пример

х=0 и х=2 – стационарные точки.

Мы уже видели, что 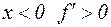при , при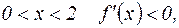

Поэтому слева от точки х=0 , справа х=0 – точка max.

Аналогично слева от точки х=2 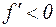, а справа 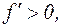х=2 – точка min (см. график).

2.

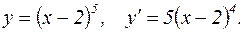
Очевидно 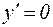при х=2. Если же 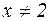, то 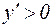, т.е. слева и справа от точки х=2 производная положительна. Экстремума нет.

График имеет вид:

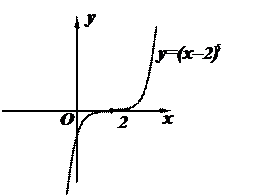Если исследовать знак первой производной слева и справа от стационарной точки затруднительно, то можно установить наличие или отсутствие экстремума по второй производной в критической точке (разумеется, если эта вторая производная существует).

Пример.

Опять возьмем 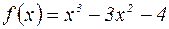. Тогда

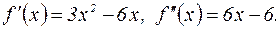
В первой критической точке х=0 отрицательный знак указывает, что 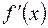в точке х=0 убывает, значит она меняет знак с «+» на «–», т.е. х=0 – точка max.

Во второй критической точке х=2 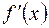в точке х=2 возрастает, т.е. меняет знак с «-» на «+». Точка х=2 – точка min.

Экстремум функции, не дифференцируемой в данной точке

До сир пор мы решали вопрос о наличии у функции f (x) экстремума в такой точке с, в которой функция f (x) дифференцируема. Теперь изучим вопрос о наличии экстремума в точке с, в которой функция не дифференцируема, но дифференцируема всюду в некоторой окрестности справа и слева от точки с.

Теорема.

Пусть функция f (x) дифференцируема всюду в некоторой окрестности точки с, за исключением, быть может, самой точки с, и непрерывна в точке с.

Тогда, если в пределах указанной окрестности производная (х) положительна (отрицательна) слева от точки с и отрицательна (положительна) справа от точки с, то функция имеет в точке с локальный максимум (минимум).

Если же производная имеет слева и справа от с одинаковый знак, то экстремума в точке с нет (без доказательства).

Графическая иллюстрация:

В случаях 1 и 2 производная меняет в точке с знак; в случае 1 с «+» на «–», функция имеет max; в случае 2 с «–» на «+», функция имеет min. В случае 3 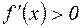и слева и справа от точки с; экстремума нет. Аналогично в случае 4 и слева и справа от точки с; экстремума также нет.

Date: 2015-09-02; view: 638; Нарушение авторских прав