Поведение функции на отрезке. Теоремы о среднем

Теорема Ролля.

Пусть функция f непрерывна на отрезке [ a,b ], имеет производную на интервале (a,b) и принимает равные значения f (a)= f (b) на концах отрезка. Тогда на интервале (a,b) есть хотя бы одна точка с, где производная от f равна нулю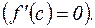

Доказательство.

Пусть M и m – соответственно максимум и минимум f на отрезке [ a,b ]. Они существуют в силу непрерывности f на [ a,b ]. Если M=m, то f (x)= M для всех 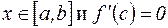в любой точке .

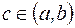Если же одно из чисел m или M отлично от чисел f (a)= f (b), (пусть для определенности 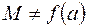), то максимум М на отрезке [ a,b ] достигается в некоторой точке 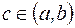интервала и следовательно, в этой точке f имеет локальный максимум. Тогда по теореме Ферма 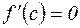. Случай 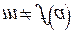разбирается аналогично. Теорема доказана.

Теорема Коши.

Пусть функции 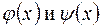непрерывны на отрезке [ a,b ] и имеют производные на интервале (a,b), причем производная 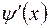не обращается в нуль. Тогда внутри этого интервала найдется точка a<c<b, такая, что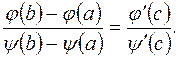

Доказательсво.

Для начала заметим, что 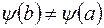, так как в противном случае по теореме Ролля производная 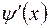обращалась бы в нуль внутри отрезка, а это противоречит условию теоремы. Таким образом, .

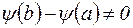Составим вспомогательную функцию

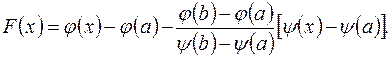
Тогда F (a) =0, F (b)=0 и функция F (x) удовлетворяет на отрезке [ a,b ] условиям теоремы Ролля. Таким образом, существует точка с, a<c<b, такая что

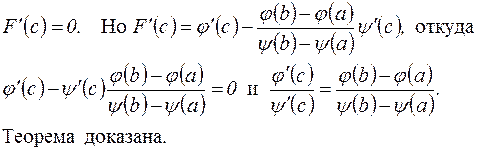
Теорема Лагранжа.

Пусть функция f(x) непрерывна на отрезке [ a,b ] и имеет производную на интервале (a,b). Тогда на этом интервале существует точка с, a<c<b, для которой выполняется равенство

(*)

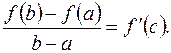Доказательство.

Теорема является следствием теоремы Коши, для этого следует положить .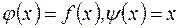

Геометрический смысл теоремы Лагранжа состоит в следующем.

Левая часть равенства 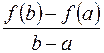есть тангенс угла наклона к оси х хорды, стягивающей точки A (a;f (a)) и B (b;f (b)) графика функции y=f (x), а правая часть есть тангенс угла наклона касательной к графику в некоторой промежуточной точке .

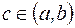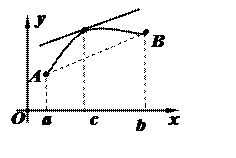
Теорема Лагранжа утверждает, что если функция непрерывна и имеет производную, то на ее графике имеется точка, в которой касательная к графику параллельна хорде, стягивающей концы кривой A (a;f (a)) и B (b;f (b)).

Равенство , записанное в виде

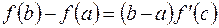
называется формулой конечных приращений Лагранжа. Иногда записывают последнюю формулу так:

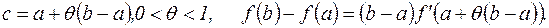
Эта формула верна как для a<b, так и для .

Date: 2015-09-02; view: 434; Нарушение авторских прав