Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Глава 4 задачи математической статистики
Основная задача математической статистики состоит в создании метода сбора и обработки статистических данных для получения научных и практических выводов. Совокупность всех объектов, подчиненных одному признаку, называется генеральной совокупностью. На практике, как правило, обследование всех объектов не производится в силу излишней трудоемкости такого процесса.. Обычно из всей совокупности отбирают ограниченное число объектов, которые и подвергают изучению. Такую случайно отобранную совокупность называют выборочной совокупностью или выборкой. Выборка, достаточно хорошо описывающая всю генеральную совокупность, называется репрезентативной (представительной). Для получения репрезентативной выборки необходимо, чтобы все отобранные элементы имели одинаковую вероятность попасть в выборку. Элементы 
, попавшие в выборку называются вариантами, а их количество n- объемом выборки. Отобранные элементы располагаются обычно в порядке возрастания. Такая последовательность вариант называется вариационным рядом. Среди n элементов выборки могут встречаться повторяющиеся. Если элемент 
встречается 
раз,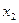 
- 
раз,……..то числа 
называются частотами вариант 
. Очевидно, что сумма всех частот равна объему выборки.
Расположенная в порядке возрастания вариант последовательность пар чисел, составленная из вариант и их частот (, ), (, ), …..(
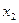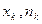) называется статистическим рядом, или статистическим распределением. При этом пользуются табличной записью.
| 
| 
| …………….. | 
|
| 
|
| …………….. | 
|
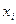
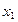
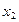
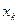
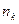
Иногда вместо частоты варианты требуется использование относительных частот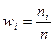 
.
В целях наглядности, строят различные графики статистического распределения. Они помогают лучше представить себе характер распределения элементов выборки, а иногда и сделать предварительные предположения о законе распределения генеральной совокупности. Такими графиками являются полигон частот и гистограмма.
Полигоном частот называется ломаная линия, вершинами которой являются точки (, ), (, 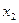), …..(), 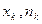определяемые элементами статистического ряда.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению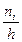 
(плотность частоты).
Эмпирической функцией распределения называют функцию 
,определяющую для каждого значения x относительную частоту события Х< x (т.е.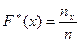 
).
ПРИМЕР 17: Время недельной загрузки электрических духовых шкафов 50 обследованных предприятий общественного питания в часах:
Построить полигон, гистограмму частот, эмпирическую функцию распределения.
Решение: Составим интервальную таблицу. Будем проводить группировку по интервалам равной длины h= 23-14=9, тогда количество интервалов равно i=(77-14)/9=7
| Номер интервала | Границы интервала | Середина интервала | частота | Относительная частота | Функция распределения |
| 14 – 23 | 18,5 | 0,04 | 0,04 | ||
| 23 – 32 | 27,5 | 0,06 | 0,1 | ||
| 32 – 41 | 36,5 | 0,12 | 0,22 | ||
| 41 – 50 | 45,5 | 0,34 | 0,56 | ||
| 50 – 59 | 54,5 | 0,2 | 0,76 | ||
| 59 – 68 | 63,5 | 0,18 | 0,94 | ||
| 68 - 77 | 72,5 | 0,06 |
По результатам группировки строим полигон частот, гистограмму частот, эмпирическую функцию распределения (рисунки 1, 2, 3).
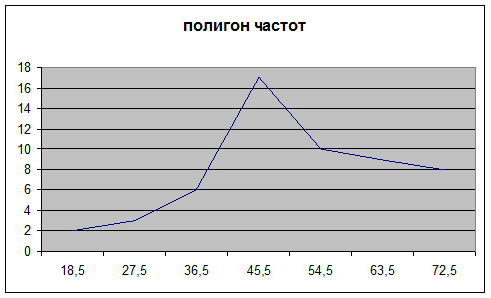рис. 1
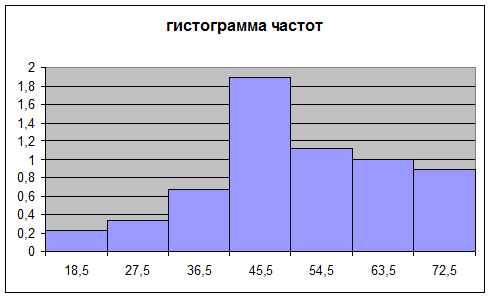рис. 2
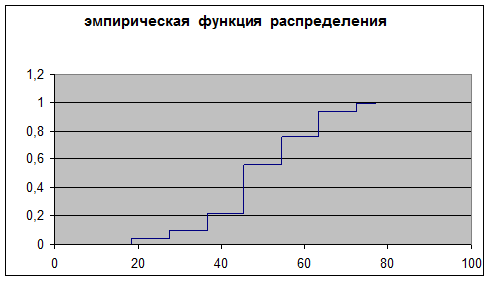рис. 3
· Точечные и интервальные оценки параметров распределения.
Предположим, что заранее известен вид теоретического распределения интересующего нас признака, но параметры этого распределения не известны и должны быть найдены по данным выборки. Задача оценивания параметров теоретического распределения состоит в построении формул, зависящих от выборочных значений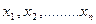 
. Любую функцию 
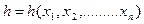, зависящую от выборки и поэтому являющуюся случайной величиной, принято называть статистикой. Для того, чтобы оценки неизвестных параметров, то есть статистики, давали хорошее приближение неизвестных параметров распределения генеральной совокупности, они должны удовлетворять определенным требованиям:
1. Математическое ожидание оценки параметра по всевозможным выборкам данного объема должно равняться истинному значению определяемого параметра. В этом случае оценку называют несмещенной.
2. При увеличении объема выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной.
Средняя выборочная, выборочные дисперсия и среднее квадратическое отклонение являются оценками параметров генеральной совокупности, выражающимися одним числом. Такие оценки называются точечными. Они могут сильно отличаться от истинной величины оцениваемого параметра. Это вызывает необходимость оценивать точность и надежность полученных оценок. Что производится при помощи интервальных оценок. Представляет интерес прежде всего доверительный интервал для оценки математического ожидания количественного признака Х генеральной совокупности распределенного по нормальному закону. При этом важны 2 случая:
1. Если заранее известна величина среднего квадратического отклонения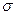 
, то границы доверительного интервала для оценки математического ожидания a имеют вид: 
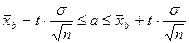, где 
определяемая по таблице для функции Лапласа Ф(t) (см. приложение 2 «Теория вероятностей и математическая статистика» В.Е. Гмурман)
2. Если среднее квадратическое отклонение исследуемого признака заранее неизвестно, то используется эмпирическое (выборочное) среднее квадратическое отклонение. В этом случае доверительный интервал для а имеет вид: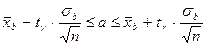 
, здесь величина 
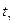определяется по таблице распределения Стьюдента для заданного объема и доверительной вероятности (см. приложение 3 «Теория вероятностей и математическая статистика» В.Е. Гмурман)
Пример 18: По данной выборке построить полигон частот. Построить 95%-ый доверительный интервал для математического ожидания и 95%-ый доверительный интервал для среднего квадратического отклонения. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности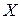 
с эмпирическим распределением.
| |||||||||||
|
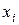
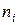
Решение:
1) Определим объем выборки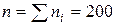 
.
2) Построим полигон частот. Для этого отложим на оси абсцисс варианты 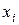, а на оси ординат – соответствующие им частоты 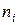, соединив точки 
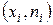отрезками прямых. Получим искомый полигон частот
3) Вычислим выборочную среднюю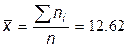 
.
4) Вычислим смещенную оценку дисперсии (выборочную дисперсию)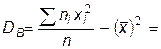 
.
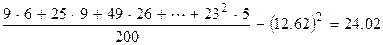5) Вычислим несмещенную оценку дисперсии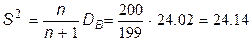 
.
6) Вычислим выборочное среднее квадратическое отклонение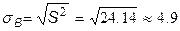 
.
7) Построим 95%-ый доверительный интервал для математического ожидания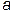 
нормально распределенного признака 
, 
; 
; 
; 
; 
; 
; 
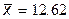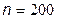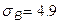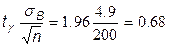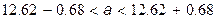8) Построим 95%-ый доверительный интервал для среднего квадратического отклонения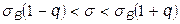 
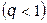
Найдем значение 
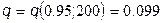
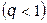
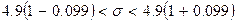
9) Используя критерий Пирсона, при уровне значимости 0.05 проверим, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределении выборки
а) вычислим теоретические частоты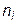 
по формуле
,
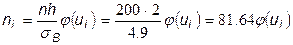где 
- объем выборки; 
- шаг (разность между двумя соседними вариантами); 
; 
.
Для вычислений составим расчетную таблицу:
| i | 
|
|
| 
| 
| 
| 
| |
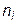
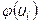
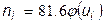
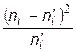
| -1.96 | 0.06 | 4.90 | 1.21 | 0.25 | ||||
| -1.55 | 0.12 | 9.79 | 0.62 | 0.06 | ||||
| -1.15 | 0.21 | 17.14 | 78.5 | 4.6 | ||||
| -0.74 | 0.30 | 24.48 | 0.27 | 0.01 | ||||
| -0.33 | 0.38 | 31.01 | 1.02 | 0.03 | ||||
| 0.08 | 0.49 | 32.64 | 44.09 | 1.35 | ||||
| 0.49 | 0.35 | 28.56 | 57.15 | 2.0 | ||||
| 0.89 | 0.27 | 22.03 | 3.88 | 0.18 | ||||
| 1.30 | 0.17 | 13.87 | 37.58 | 2.71 | ||||
| 1.71 | 0.09 | 7.34 | 0.44 | 0.06 | ||||
| 2.12 | 0.04 | 3.26 | 3.03 | 0.93 |
б) вычислим наблюдаемое значение критерия
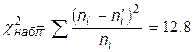
в) по таблице критических точек распределения 
по заданному уровню значимости и числу степеней свободы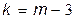 
((
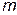- число групп выборки), в нашем случае 
, 
) находим критическую точку
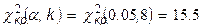
г) т.к.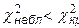 
, то нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности.
Замечание. Значения 
можно взять из таблиц приложений в "Руководстве к решению задач по теории вероятностей и математической статистике" В.Е.Гмурмана (М.: 1990 г.)
· К о э ф ф и ц и е н т к о р р е л я ц и и.
Величина М[(x-Мx) (h-Мh)] называется ковариацией случайных величин x и h, cov (x, h). Если (x, h) - непрерывная двумерная случайная величина с плотностью распределения р (x, y), то
 |
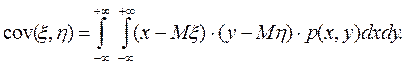Величина r=cov(x,h)/ÖDxDh называется коэффициентом корреляции случайных величин x и h.
Свойства коэффициента корреляции.
10. Модуль коэффициента корреляции не превосходит единицы, | r | £ 1.
20. Если x и h независимые случайные величины, то r = 0.
Обратное неверно: из условия r = 0 (некоррелированность случайных величин x и h) не следует независимость x и h.
30. Если x и h связаны линейной зависимостью, то | r | = 1.
Date: 2015-09-02; view: 1592; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |