Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
И их числовые характеристики
· О п р е д е л е н и е и в и д ы с л у ч а й н ы х в е л и ч и н.
Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, заранее неизвестное.
Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями. Число таких значений может быть конечным или бесконечным.
Случайная величина называется непрерывной, если все ее возможные значения заполняют некоторый конечный или бесконечный интервал. Очевидно, что число таких значений бесконечно.
Обозначаются случайные величины заглавными латинскими буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами х1, х2, у1,…
· З а к о н р а с п р е д е л е н и я в е р о я т н о с т е й
д и с к р е т н о й с л у ч а й н о й в е л и ч и н ы.
Законом распределения дискретной случайной величины называется соответствие между возможными значениями и их вероятностями. Его можно задать с помощью таблицы, аналитически (в виде формулы) и графически.
Таблица, задающая закон распределения дискретной случайной величины, имеет вид: Х х1 х2 … хn
Р р1 р2 … рn
В верхней строке таблицы перечислены возможные значения дискретной случайной величины, а во второй – их вероятности. Так как события Х=х1, Х=х2, …, Х=хn образуют полную группу (докажите!), то сумма вероятностей второй строки равна единице: р1+ р2+…+ рn= 1.
Закон распределения дискретной случайной величины можно изобразить графически. Для этого в прямоугольной системе координат строят точки с координатами (х1,р1), (х2,р2), …,(хn,рn) и соединяют их последовательно отрезками. Полученную ломаную называют прямоугольником распределения.
К основным законам распределения вероятностей дискретной случайной величины относятся биномиальный закон (задается формулой Бернулли), геометрический закон, гипергеометрический закон, закон Пуассона. Изучите §4,5,6,7,8 гл. VI [1].
·М а т е м а т и ч е с к о е о ж и д а н и е и д и с п е р с и я
д и с к р е т н о й с л у ч а й н о й в е л и ч и н ы.
Математическим ожиданием случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
М(Х)=х1р1+х2р2+х3р3+…+хnрn
Если дискретная случайная величина принимает бесконечное число значений,
то 
М(Х)= 
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. В этом заключается вероятностный смысл математического ожидания.
Изучите свойства математического ожидания (см. §4 гл. VII [1]).
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X)= M (X-M(X))2.
Более удобна для вычисления другая формула, которая выводится из определения дисперсии:
D(X)= M(X2) - M(X)2
где M(X2)= 
Дисперсия характеризует степень рассеяния возможных значений случайной величины вокруг ее среднего значения.
Изучите свойства дисперсии (см. §4,5 гл. VII [1]).
Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии: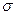 
(Х)= 
.Данная оценка рассеяния имеет ту же размерность, что и случайная величина, поэтому более удобна в применении, чем дисперсия.
Изучите также начальные и центральные теоретические моменты (см. §10 гл. VIII [1]).
Пример 12. Закон распределения дискретной случайной величины имеет вид:
| Х | ||||
| Р | 0,2 | 0,1 | 0,1 | 0,6 |
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение: М(Х)= х1р1+х2р2+х3р3+…+хnрn
В нашем примере n=4, М(Х)= х1р1+х2р2+х3р3+х4р4
М(Х)=3∙0,2+4∙0,1+5∙0,1+6∙0,6=5,1
D(X)= M(X2) - M(X)2
Вычислим M(X2)= х12р1+х22р2+х32р3+х42р4
=32∙0,2+42∙0,1+52∙0,1+62∙0,6=27,5.
D(X)= 27,5-5,12=1,49
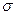(Х)= ≈ 1,22
Ответ: М(Х)=5,1; D(X)=1,49; 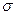(Х) ≈ 1,22.
Пример 13. Дан перечень возможных значений дискретной случайной величины Х: x1=2, x2=3, а также известно математическое ожидание Х: М(Х)=2,6.
Найти вероятности р1 и р2, соответствующие возможным значениям х1 и х2.
Решение: пользуясь тем, что сумма вероятностей всех возможных значений Х равна единице, а также принимая во внимание, что М(Х)=2.6, составим систему линейных уравнений относительно неизвестных вероятностей:
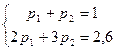
Решив эту систему, найдем р1=0,4; р2=0,6.
Ответ: р1=0,4; р2=0,6.
· Ф у н к ц и я р а с п р е д е л е н и я в е р о я т н о с т е й
с л у ч а й н о й в е л и ч и н ы.
Функцией распределения (или интегральной функцией распределения) называют функцию F(х), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.
F(х)=Р(Х<х).
Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Функция распределения дискретной случайной величины –ступенчатая функция, то есть, разрывная. Функция распределения непрерывной случайной величины – непрерывная функция.
Изучите свойства функции распределения и познакомьтесь с ее графиком (см. §2,3 гл. Х [1]).
При решении задач очень важна формула, позволяющая вычислить вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале (а,b):
Р(а≤Х<b)=F(b)-F(a)
Обратите внимание, что для непрерывной случайной величины вероятность того, что Х примет одно определенное значение, равна нулю, поэтому следующие вероятности равны: Р(а≤Х<b) = Р(а≤Х≤b)= Р(а<Х≤b)= Р(а<Х<b) = =F(b)-F(a).
· П л о т н о с т ь р а с п р е д е л е н и я в е р о я т н о с т е й
н е п р е р ы в н о й с л у ч а й н о й в е л и ч и н ы.
Плотностью распределения вероятностей непрерывной случайной величины (или дифференциальной функцией распределения) называют производную от функции распределения:
f(x)=F '(x).
Вероятность того, что случайная величина примет значение, заключенное в интервале (а,b), равна определенному интегралу от плотности распределения в пределах от а до b:
Р(а<Х<b)=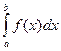 
.
Зная плотность распределения f(х), можно найти функцию распределения F(x) по формуле
F(x)=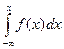 
.
Изучите свойства плотности распределения (см. §4 гл. ХI [1]).
Математическое ожидание непрерывной случайной величины находится по формуле М(Х)=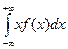 
, а дисперсия D(X)= M(X2) - M(X)2, где
М(Х2)=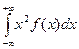 
. Среднее квадратическое отклонение 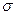(Х)= . Все свойства математического ожидания и дисперсии дискретной случайной величины переносятся на случай непрерывной случайной величины.
Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются, например, законы равномерного, нормального и показательного распределений.
Изучите закон равномерного распределения вероятностей (см. §6 гл. ХI [1]).
Date: 2015-09-02; view: 602; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |