
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 2 элементы теории вероятностей. Случайные события
|
|
Основными понятиями теории вероятности являются понятия события и вероятности событий.
Под событием понимают такой результат эксперимента или наблюдения, который при реализации комплекса условий может произойти или не произойти.
События можно подразделить на три вида:
1) достоверное - если оно при осуществлении комплекса условий обязательно
произойдёт;
2) невозможное - если оно при испытании не может произойти;
3) случайное - если при испытании оно может произойти, а может и не произойти.
· К л а с с и ч е с к о е о п р е д е л е н и е в е р о я т н о с т и.
Вероятностью события А называют отношение числа m благоприятствующих исходов к числу n всех возможных элементарных исходов в данном испытании.
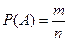
вероятность любого события А удовлетворяет неравенствам
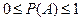
Изучите понятия относительной частоты и статистической вероятности (см. §6,7 гл.I [1]).
· Т е о р е м ы с л о ж е н и я и у м н о ж е н и я в е р о я т н о с т е й.
События 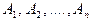 называются совместными, если появление одного из них не исключает возможности появления других.
называются совместными, если появление одного из них не исключает возможности появления других.
Например: 3 орудия стреляют в цель и возможность попадания в цель всех 3-х орудий не исключается, следовательно они совместны.
События 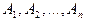 называются несовместимыми (несовместными), если появление одного из них исключает возможность появления других.
называются несовместимыми (несовместными), если появление одного из них исключает возможность появления других.
Например: при бросании монеты выпадение «орла» исключает возможность появления "решки".
Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Теорема сложения вероятностей:
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Р (А+В)= Р (А)+ Р (В)
(доказательство см. §1 гл.II [1]).
В случае, когда события А и В совместны, вероятность их суммы выражается формулой:
Р (А+В)= Р (А)+ Р (В)- Р (АВ), где АВ - произведение событий А и В.
Теорема сложения вероятностей для нескольких событий:
Вероятность суммы нескольких несовместных событий равна сумме их вероятностей:
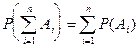
В случае, когда события 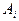 совместны, вероятность их суммы выражается формулой
совместны, вероятность их суммы выражается формулой
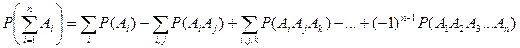 ,
,
где суммы распространяются на все возможные комбинации различных индексов i, j, k,...., взятых по одному, по два, по три и т.д.
Пример 1. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
Решение. Обозначим события:
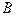 – появление хотя бы одного туза,
– появление хотя бы одного туза,
А 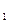 – появление одного туза,
– появление одного туза,
А 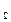 – появление двух тузов,
– появление двух тузов,
А 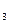 – появление трех тузов.
– появление трех тузов.
Событие 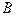 произойдет, если наступит одно из несовместимых событий А
произойдет, если наступит одно из несовместимых событий А 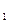 , А
, А 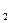 или А
или А 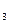 .
.
Очевидно, что В = А 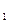 + А
+ А 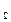 + А
+ А 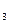 ,
,
Р (В) = Р (А 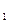 ) + Р (А
) + Р (А 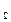 ) + Р (А
) + Р (А 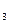 ),
),
т.е. Р (В) = 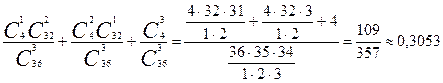 .
.
Можно решить иначе. Событие 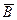 , противоположное событию
, противоположное событию 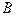 , состоит в том, что среди вынутых из колоды карт нет ни одного туза:
, состоит в том, что среди вынутых из колоды карт нет ни одного туза:
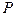 (
(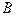 ) +
) + 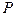 (
(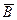 ) = 1,
) = 1,
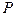 (
(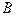 ) = 1 -
) = 1 - 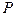 (
(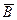 ) =
) = 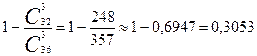 .
.
Пример 2. В урне находятся 5 белых и 4 черных шара. Из урны вынимают наугад 3 шара.
Какова вероятность того, что они окажутся одного цвета?
Решение. Обозначим события:
А – появление трех шаров одного цвета,
А 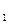 – появление трех шаров белого цвета,
– появление трех шаров белого цвета,
А  – появление трех шаров черного цвета.
– появление трех шаров черного цвета.
Событие А наступит, если произойдет какое-нибудь из двух несовместных событий А 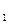 или А
или А 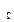 :
:
А = А 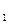 + А
+ А 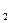 ,
,
Р (А) = Р (А 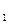 ) + Р (А
) + Р (А 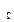 ) =
) = 
Замечание. Если событие А и В совместны, то
Р(А + В) 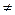 Р(А) + Р(В).
Р(А) + Р(В).
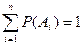 |
Если события
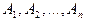 несовместны и образуют полную группу, то сумма их вероятностей равна единице:
несовместны и образуют полную группу, то сумма их вероятностей равна единице:
Событие 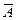 называется противоположным событию
называется противоположным событию 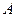 , если оно состоит в непоявлении события
, если оно состоит в непоявлении события 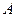 .
.
Сумма вероятностей противоположных событий равна единице:
Р (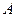 ) + Р (
) + Р (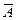 ) = 1.
) = 1.
Условной вероятностью события А при наличии В называется вероятность события А, вычисленная при условии, что событие В произошло. Эта вероятность обозначается Р 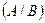 .
.
События А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий
Р 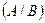 = Р (
= Р (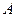 ); Р
); Р 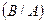 = Р (В).
= Р (В).
Date: 2015-09-02; view: 683; Нарушение авторских прав