
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Т е о р е м а у м н о ж е н и я в е р о я т н о с те й
|
|
д л я н е с к о л ь к и х с о б ы т и й
Р  = Р
= Р  Р
Р 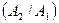 Р
Р 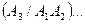 Р
Р 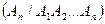
В случае, когда события независимы, т. е. появление любого числа из них не меняет вероятностей появления остальных,
Р 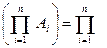 Р
Р 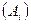 .
.
Пример3. В урне 5 белых и 2 черных шара. Из нее извлекают наугад 3 шара. Найти вероятность того, что при первом извлечении появится белый шар (событие А 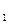 ), при втором – снова белый шар (событие А
), при втором – снова белый шар (событие А  ) и при третьем – черный (событие В).
) и при третьем – черный (событие В).
Решение. События А 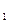 , А
, А  и В – зависимые. Нас интересуют появление и события А
и В – зависимые. Нас интересуют появление и события А 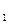 , и события А
, и события А  , и события В, т.е. их произведение А
, и события В, т.е. их произведение А 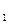 А
А  В. Тогда имеем
В. Тогда имеем
Р 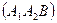 = Р
= Р  Р
Р 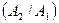 Р
Р 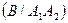 =
=  .
.
Пример 4. Те же условия, что и в предыдущем примере, но каждый раз шары возвращаются в урну и все шары в урне перемешиваются.
Решение. По условию задачи события А 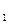 , А
, А  и В – независимые. Тогда имеем
и В – независимые. Тогда имеем
Р 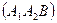 = Р
= Р  Р
Р 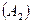 Р
Р  =
=  .
.
Пример 5. На семи одинаковых карточках написаны буквы а, а, в, о, р, с, т. какова вероятность того, что
1) извлекая все карточки по одной наудачу, получим в порядке их выхода слово «Саратов»;
2) извлекая пять карточек по одной наудачу, получим в порядке их выхода слово «товар»?
Решение.
1) Обозначим через 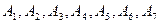 события «появления букв» с, а, р,а, т, о, в соответственно. События
события «появления букв» с, а, р,а, т, о, в соответственно. События 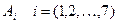 - зависимые. Нас интересует появление события
- зависимые. Нас интересует появление события  .
.
Тогда получим

2) Обозначим через  события «появления букв» т, о, в, а, р соответственно. Найдем вероятность события
события «появления букв» т, о, в, а, р соответственно. Найдем вероятность события 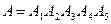
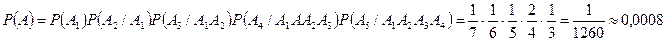 .
.
Пример 6. Три стрелка стреляют в цель независимо друг от друга. Вероятность попадания в цель для первого стрелка равна 0,6, для второго – 0,7 и для третьего – 0,8. Найти вероятность того, что произойдут два попадания в цель, если каждый стрелок сделает по одному выстрелу.
Решение. Обозначим через А событие, состоящее в том, что произойдут два попадания в цель, если каждый из трех стрелков сделает по одному выстрелу. Через В, С, D обозначим попадание в цель соответственно первым стрелком; вторым и третьим; 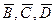 - промахи первым, вторым и третьим стрелком.
- промахи первым, вторым и третьим стрелком.
Очевидно, что
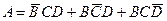 .
.
Применив теоремы сложения и умножения вероятностей, получим

Здесь воспользовались свойством противоположных событий, например, 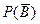 нашли из равенства Р(В) +
нашли из равенства Р(В) + 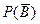 = 1.
= 1.
Изучите правило нахождения вероятности хотя бы одного события (см. §5 гл.III [1]).
· Г е о м е т р и ч е с к и е в е р о я т н о с т и.
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок 1 пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством
Р = Длина 1/ Длина L.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от её расположения относительно G, ни от формы g, то вероятность попадания точки в фигуру g определяется равенством
Р = Площадь g / Площадь G.
Аналогично определяется вероятность попадания точки в пространственную фигуру v, которая составляет часть фигуры V:
Р = Объём v / Объём V.
· Ф о р м у л а п о л н о й в е р о я т н о с т и.
Формула полной вероятности. Пусть событие В может произойти только вместе с одним из событий 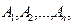 которые образуют полную систему событий. Известны вероятности этих событий
которые образуют полную систему событий. Известны вероятности этих событий 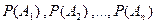 и условные вероятности события В
и условные вероятности события В 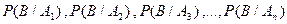
Date: 2015-09-02; view: 523; Нарушение авторских прав