Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Докажем, что
|
|
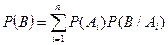
Действительно, событие В может появиться только с одним из несовместных событий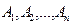 
, образующих полную систему событий. Иначе говоря,
,
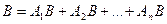где события 
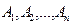несовместны, что следует из несовместности событий . Найдем вероятность события В:
,
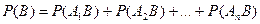отсюда
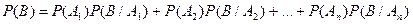
что и требовалось доказать. Доказанная формула называется формулой
п о л н о й в е р о я т н о с т и.
· Ф о р м у л а Б а й е с а.
Пусть по-прежнему имеет место равенство
.
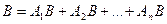Найдем вероятность события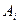 
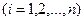при условии, что событие В произошло:
,
отсюда
.
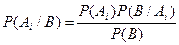Воспользовавшись формулой 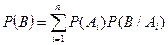, окончательно получим
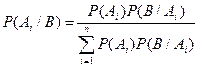- эта формула называется формулой Б а й е с а или формулой в е р о я т н о с т и г и п о т е з.
Формула Байеса дает возможность произвести переоценки вероятностей
событий (гипотез)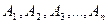 
после того, как стало известно, что событие В наступило.
Пример 7. Электролампы изготовляются на двух заводах. Первый завод производит 60% общего количества электроламп, второй – 40 %. Продукция первого завода содержит 70 % стандартных ламп, второго – 80 %. В магазин поступает продукция обоих заводов. Какова вероятность того, что купленная в магазине лампа окажется стандартной?
Решение. Обозначим через В событие, состоящее в том, что куплена стандартная лампа,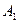 
- что лампа изготовлена на первом заводе, 
- на втором. Из условия задачи
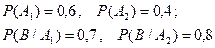
По формуле полной вероятности имеем
.
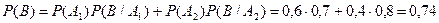Пример 8. Пусть выполняется условие примера 1. Предположим, что электролампа куплена и оказалась стандартной. Найти вероятность того, что лампа изготовлена на первом заводе.
Решение. Воспользовавшись формулой Байеса и результатами примера 1, получим
.
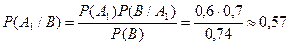Заметим, что до испытания вероятность этой гипотезы 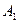равнялась 0,6, а после испытания вероятность этой гипотезы стала равняться 0,57 (при условии, что произошло событие В).
Пример 9. Имеется 6 урн со следующим составом шаров:
2 урны – 3 белых и 6 черных (состав );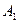
3 урны – 3 белых и 2 черных (состав );
1 урна – 4 белых и 1 черный (состав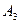 
).
Наугад выбирается урна и из нее извлекается один шар.
а) Чему равна вероятность того, что шар окажется белым (событие В)?
б) Найти вероятность гипотезы при условии, что произошло событие В.
Решение. а) Вероятности гипотез , ,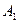
.
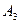
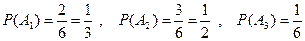Условные вероятности события В
.
По формуле полной вероятности
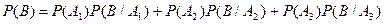получим
.
б) По формуле Байеса найдем условную вероятность гипотезы :
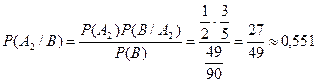
· П о в т о р е н и е и с п ы т а н и й. Ф о р м у л а Б е р н у л л и.
Если производится n независимых испытаний, в каждом из которых вероятность появления события А равно p, то вероятность того, что событие А появится в этих n испытаниях m раз выражается формулой Бернулли
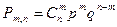, где q = 1 - р
Вероятность того, что в n испытаниях событие наступит
а) менее k раз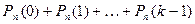 
б) более k раз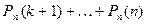 
в) не менее k раз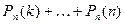 
г) не более k раз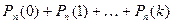 
Если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям, в этих случаях применяют локальную теорему Лапласа
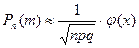
где 
, 
(см. таблицу приложений)
для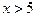 
считают, что 
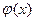- четная функция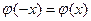 
Если вероятность появления события А в каждом из n независимых испытаний мала, а число испытаний велико, то
- асимптотическая формула Пуассона
где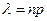 
.
Формулу эту применяют тогда, когда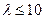 
Пример 10: Всхожесть семян данного растения составляет 90 %. Найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.
Решение. Воспользуемся формулой Бернулли. Если производится n независимых испытаний, при каждом из которых вероятность осуществления события А постоянна и равна р, а вероятность противоположного события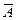 
равна q=1-p, то вероятность 
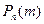того, что при этом событие А осуществляется ровно т раз, вычисляется по формуле
,
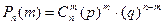где 
есть число сочетаний из n элементов по m.
а) По условию задачи вероятность всхожести семян р= 0,9; тогда q= 0,1; в данном случае n= 5 и m = 4. Подставляя эти данные в формулу Бернулли, получим
б) Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом,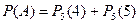 
. Первое слагаемое уже найдено. Для вычисления второго снова применяем формулу Бернулли:
.
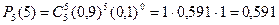Следовательно, Р(А) = 0,328 + 0,591 = 0,919.
Пример 11: Вероятность появления события А в каждом из 625 испытаний равна 0,64. Найти вероятность того, что событие А в этих испытаниях появится ровно 415 раз.
Решение. Если число испытаний п велико, то применение формулы Бернулли приводит к громоздким вычислениям. Использование этой формулы становится практически невозможным. В таких случаях применяют приближенную формулу, которая выражает локальную теорему Лапласа.
Если вероятность наступления события А в каждом из п независимых испытаний постоянна и равна р (р отлично от нуля и единицы), а число п достаточно велико, то вероятность 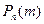того, что в этих испытаниях событие А наступит т раз (безразлично в какой последовательности) вычисляется приближенно по формуле
,
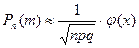где , а
Имеются готовые таблицы значений функции 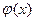(см. таблицу приложения 1, [1]).
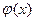Для x >5 считают, что . Так как функция четная, то 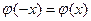. По условию задачи п = 625, т = 415, р = 0,64. Находим q = 1-0.64 = 0.36. Определяем значение x при этих данных:
.
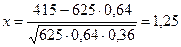По таблице находим, что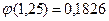 
. Подставив это значение в формулу, получим:
.
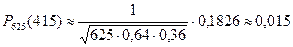Date: 2015-09-02; view: 510; Нарушение авторских прав