Операции t- и s-норм над нечеткими множествами

Триангулярной или так называемой t-нормой нечетких множеств, определенных на нечетком множестве Х, называется двуместная действительная операция (функция) типа:

отвечающая следующим свойствам:

· Ограниченность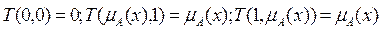

· Монотонность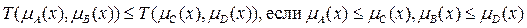

· Коммутативность

· Ассоциативность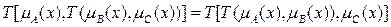

Примером Т-нормы может быть операция:

· Стандартная операция пересечения

· Алгебраическое произведение

· Граничное произведение

· Драстическое произведение

S-нормой над нечеткими множествами, определенными на универсальном множестве Х, называется двуместная функция 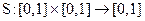, удовлетворяющая следующим свойствам:

· Ограниченность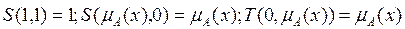

· Монотонность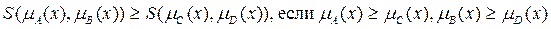

· Коммутативность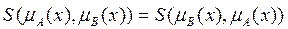

· Ассоциативность

Наиболее используемыми примерами S-норм могут быть:

2) Стандартное нечеткое объединение

2) Алгебраическая (вероятностная) сумма

2) Граничная сумма

2) Драстическая сумма

Легко показать что всегда выполняется:

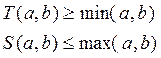
При этом существуют операторы, преобразующие оператор s в оператор t-норм.
6. Показатели неопределенности (размытости) нечетких множеств.

Существует 2 подхода к определению неопределенности:

1. Показатели размытости могут интерпретироваться как показатели неопределенности, противоположности и так далее объектов, обусловленные неполной или частичной принадлежностью объектов к некоторому множеству или классу. Этот подход используется для решения задач классификации объектов.

2. Показатели размытости рассматриваются как мера отличия нечеткого множества от обычного четкого множества.

Существует 2 основных подхода к определению показателей размытости:

1) Аксиоматический – в этом подходе показатель размытости определяется как мера неопределенности объекта х множества Х по отношению к некоторому свойству А. При этом неопределенность объекта определяется в том что он в разной степени принадлежит к классу объектов обладающих этим свойством, и к классу не обладающих. Неопределенность максимальна, если степени принадлежности равны. Неопределенность минимальна, когда объект принадлежит к 1 классу. Показатель размытости можно определить в виде некоторого функционала 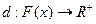удовлетворяющий следующим условиям:

1)

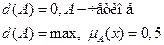
2)

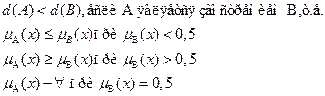
3)

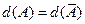
4)

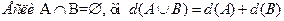
Можно доказать, что вещественный функционал является показателем размытости тогда и только тогда, если он допускает представление:

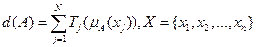
T_j­ – вещественнозначные функции от 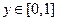, такие что T_j(0)=0, T_j­(y)= T_j­(1-y), T_j­(y) – строго возрастает на интервале [0,0.5]

_­N – число элементов в множестве Х.

Примеры показателей размытости при аксиоматическом подходе:

1. Энтропия нечеткого множества: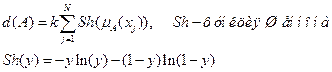

2.

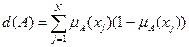
2) Метрический

Показатель размытости нечетких множеств можно определить с помощью метрики как меру отличия нечеткого множества от ближайшего к нему обычного множества. Другой способ задания показателя размытости с помощью метрики — это определение его с помощью расстояния до максимального размытого множества и расстояния между нечетким множеством и его дополнением.

Множество, ближайшее к нечеткому множеству А, называется множество 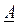, такое что

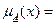
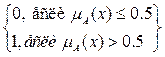
Показателем размытости называется функционал

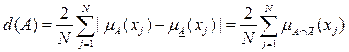
Если вместо расстояния Хэмминга использовать евклидово расстояние, то получим

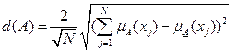
Еще одним способом является нахождения расстояния между нечетким множеством и его дополнением.

Помимо рассмотренных подходов, нашли развитие так же и другие подходы.

В ряде случаев удобно использовать возможности пребывания системы в различных состояниях.

Пусть существует N состояний системы и с ними связаны вероятности пребывания системы в этих состояниях, тогда Энтропия системы определяется следующим выражением:

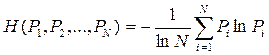
Если задано нечеткое множество А в виде совокупности пар

То выражение энтропии для оценки его нечеткости можно задать следующим образом:

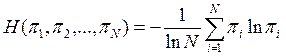
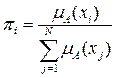
Date: 2015-08-24; view: 3007; Нарушение авторских прав