Нечеткое пересечение (fuzzy intersection)

Нечеткое пересечение нечетких множеств А и В определенных на универсальном множестве Х, определяется двуместной функцией I:[0,1] -> [0,1], аргумент которой показывает включения элемента х, одновременно в множества А и В.

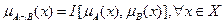
Свойства:

1. Ограниченность: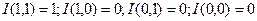

2. Коммутативность:

3. Монотонность: если 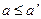и , то I (a,b) 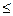I (a’,b’)

4. Ассоциативность: I (I (a,b),c)= I (a, I (b,c))

5. I – непрерывная функция

6. Идемпотентность: I (a, a)= a

В качестве примеров операции нечеткого пересечения можно использовать(я бы не стал писать это):

1) Стандартное нечеткое пересечение, т.е.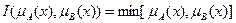

2) Так же можно рассмотреть нечеткое пересечение Ягера:

,

Очевидно что при w=1 операция пересечения будет представлять собой:

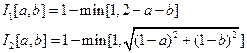
И при 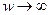– – 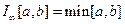стандартная операция пересечения.

{Нечеткое пересечение удовлетворяет аксиомам 1-5, но не удовл. 6}

3) Алгебраическое (вероятностное) произведение: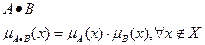

Здесь выполняются свойства коммутативности, ассоциативности, тождественности и законы де Моргана.

4) Граничное произведение:

Данная операция идентична операции нечеткого пересечения Ягера при w=1.

Для этой операции выполняются свойства коммутативности, ассоциативности, тождественности, законы де Моргана и не выполняются свойства идемпотентности и дистрибудивности.

5) Драстическое(сильное) произведение

6) Произведение Хамахера.

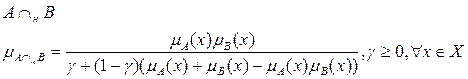
7) Лямбда-сумма.

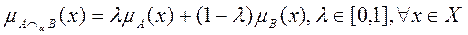
Date: 2015-08-24; view: 525; Нарушение авторских прав