Теорема 1.12

1. Диагональная форма квадратной диагонализируемой матрицы определена однозначно с точностью до перестановки диагональных элементов.

2. Если 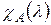раскладывается на линейные множители и не имеет кратных корней, тогда матрица 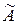является диагонализируемой.

3. Линейный оператор A имеет в некотором базисе диагональную матрицу тогда и только тогда, когда все корни его характеристического многочлена принадлежат данному полю и их геометрические кратности равны алгебраическим.

Теорема 1.13 Пусть собственные значения 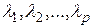оператора А различны. Тогда отвечающие им собственные векторы 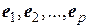линейно независимы.

Следствие. Если характеристический многочлен оператора А имеет 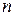различных корней, то в некотором базисе матрица оператора А имеет диагональный вид.

Действительно, в рассматриваемом случае, согласно только что сформулированной теореме собственные векторы линейно независимы и поэтому могут быть выбраны в качестве базисных. Но тогда по теореме 1.9 в этом базисе матрица оператора А будет диагональной.

Алгоритм приведения матрицы 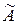к диагональному виду

1. Сначала проверим матрицу 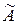на диагонализируемость. Для этого вычислим характеристический многочлен 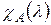матрицы 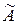и попробуем разложить его на линейные множители. Если это невозможно, то делаем вывод, что матрица 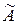не является диагонализируемой. Для каждого собственного значения , кратность которого больше 1, найти дефект матрицы 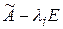. 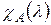Если для каждого такого собственного значения полученный дефект совпадает с кратностью в , матрица 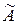является диагонализируемой. 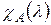Если хотя бы для одного полученный дефект будет меньше кратности в , матрица 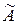не является диагонализируемой.

2. Если матрица является диагонализируемой, то найти все ее собственные векторы.

3. Диагональная форма 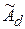матрицы 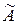и матрица перехода 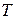записываем таким образом: начиная с левого верхнего угла по диагонали в матрицу 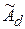записывается первое собственное число столько раз, какова его кратность. Одновременно, начиная слева, в матрицу 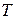по столбцам записываются координаты найденных векторов, являющиеся базисом собственного подпространства матрицы 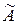(собственные векторы), соответствующие первому собственному числу. И так далее для второго, … собственных чисел.

Пример Приведите к диагональному виду матрицу

.

Решение. Характеристический многочлен матрицы: . Разложение этого многочлена на линейные множители зависит от выбора поля. Если рассматривать поле действительных чисел, то квадратный делитель 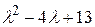многочлена 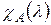не имеет действительных корней, а значит многочлен 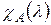не раскладывается над полем действительных чисел на линейные множители, откуда следует, что матрица не является диагонализируемой над полем действительных чисел.

Теперь рассмотрим случай поля комплексных чисел. Тогда . Многочлен разложился на простые множители, из чего следует, что матрица является диагонализируемой над полем комплексных чисел.

Собственные числа и соответствующие собственные векторы имеют вид:

, ; , ; , .

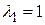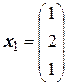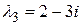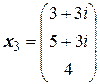Итак, диагональная форма 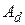матрицы и матрица перехода 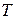будут иметь вид:

, .

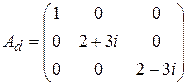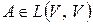– оператор с простым спектром, если , где 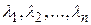различны.

1.5 Корневые подпространства

Пусть – собственное значение оператора алгебраической кратности 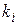. Тогда корневое подпространство, соответствующее этому собственному значению, есть ядро линейного оператора : .

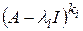Корневое подпространство является инвариантным (см. ниже) подпространством линейного оператора A. Если характеристический многочлен имеет каноническое разложение над данным полем

,

то пространство раскладывается в прямую сумму корневых подпространств:

.

В этом случае объединение базисов всех корневых подпространств даст базис всего пространства . В этом базисе матрица линейного оператора A является клеточно-диагональной. Для размерности корневого подпространства имеет место следующее часто применяемое свойство

.

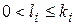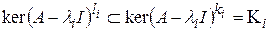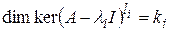Заметим, что для любого имеет место вложение подпространств . При этом, если для некоторого , размерности равны , то равны и подпространства , и, следовательно, для нахождения 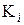, в этом случае достаточно линейный оператор возвести лишь в степень.

1.6 Жорданова нормальная форма

Пусть – конечномерное линейное пространство над полем комплексных чисел.Квадратная матрица 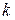-го порядка

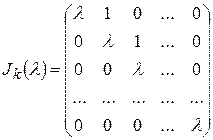
называется жордановой клеткой, соответствующей комплексному числу λ.

Жорданова матрица – это матрица 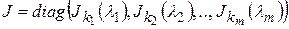с жордановыми клетками 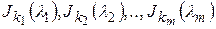на диагонали.

Корневым подпространством матрицы , соответствующим собственному числу 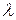, называется множество всех тех векторов , для которых .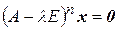

Цепным базисом корневого подпространства матрицы (жордановым базисом), соответствующим собственному числу 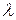, называется такой его базис 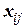, , 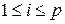, 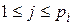для которого и .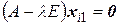

Свойства корневых подпространств и цепных базисов:

Date: 2015-08-24; view: 907; Нарушение авторских прав