Таким образом, согласно доказанному выше утверждению условие является необходимым и достаточным для того, чтобы оператор А имел обратный

Образом линейного оператора А называется множество всех элементов 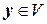, представимых в виде 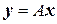. Образ линейного оператора А обозначается символом .

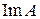Замечание 1 Отметим, что если 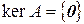, то 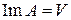, и наоборот. Поэтому наряду с отмеченным выше условием 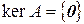условие 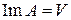также является необходимым и достаточным для того, чтобы оператор А имел обратный.

Замечание 2 Очевидно, ядро 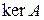и образ 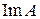– линейные подпространства пространства V.

Вследствие замечания 2 можно рассматривать размерност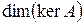и и 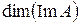этих подпространств.

Назовем рангом линейного оператора А число, обозначаемое символом 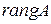и равное 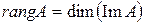. Назовем дефектом линейного оператора А число, обозначаемое символом 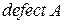и равное .

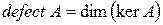Пример Пусть V – -мерное комплексное или вещественное линейное пространство.

1) Тождественный оператор 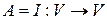, при этом , тогда 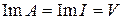, (ядро состоит из единственного нулевого элемента), значит .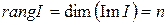

2) Нулевой оператор 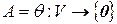, тогда , , , .

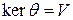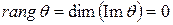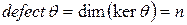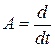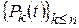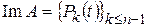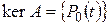3) Рассмотрим оператор дифференцирования на пространстве многочленов степени не выше , тогда , (т.к. 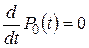), отсюда , .

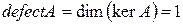Теорема 1.2 Пусть размерность пространства V равна , и пусть А – линейный оператор из 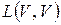. Тогда .

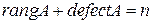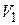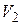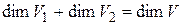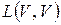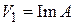Теорема 1.3 Пусть и – два таких подпространства n-мерного пространства V, что . Тогда существует такой линейный оператор А из , что и .

Следствие из теоремы 1.2. Для того чтобы оператор А из 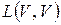имел обратный 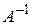, необходимо и достаточно, чтобы .

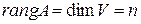Пусть А и В – линейные операторы из 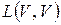. Справедлива следующая теорема.

Теорема 1.4 Имеют место следующие соотношения:

, .

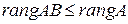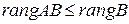Теорема 1. 5 Пусть А и В – линейные операторы из 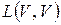и – размерность V. Тогда .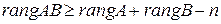

Следствие из теорем 1.4 и 1.5. Если 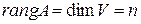, то .

1.2 Матричная запись линейных операторов

Фиксируем в линейном пространстве V базис 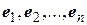. Пусть – произвольный элемент V и

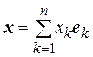(1.11)

разложение по данному базису.

Пусть А – линейный оператор из 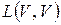. Тогда из (1.11) получаем

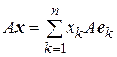. (1.12)

Полагая

(1.13)

перепишем (1.12) в следующей форме:

.

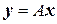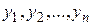Таким образом, если и элемент имеет координаты , то

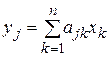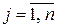, . (1.14)

Рассмотрим квадратную матрицу 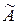с элементами 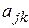: . Эта матрица называется матрицей линейного оператора в заданном базисе 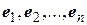. Иначе, элементами матрицы оператора являются координаты образов базисных векторов под действием оператора, записанные в столбцы.

Замечание 1 Если оператор А нулевой, то все элементы матрицы 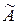этого оператора равны нулю в любом базисе, т.е. 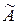– нулевая матрица.

Замечание 2 Если оператор А единичный, т.е. 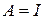, то матрица этого оператора будет единичной в любом базисе.

Пример Оператор переводит вектор 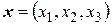в вектор 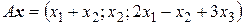. Определить, является ли оператор линейным. Если да, то записать его матрицу.

Решение. Пусть , тогда . Будем иметь

,

, .

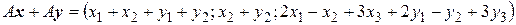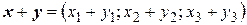Видим, что .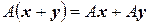

, ,

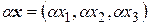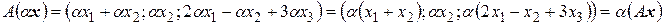т.е. 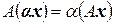. Оба свойства выполнены, поэтому оператор является линейным.

Для нахождения матрицы этого оператора вычислим координаты базисных векторов 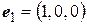, , 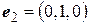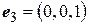под действием оператора :

, , .

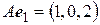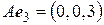Запишем полученные координаты в виде столбцов матрицы:

.

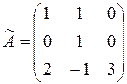Пример В пространстве матриц второго порядка с обычными операциями сложения матриц и умножения матриц на число действует линейный оператор по правилу 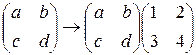. Найти матрицу этого линейного оператора в базисе , , , .

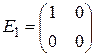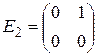Решение. Найдем образы базисных векторов под действием линейного оператора:

,

,

,

.

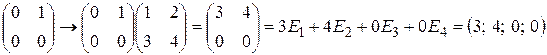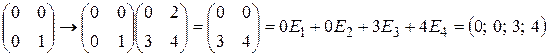Тогда матрица линейного оператора имеет вид: .

Мы выяснили, что каждому линейному оператору А из 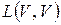при заданном базисе линейного пространства V отвечает матрица 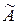этого оператора. Естественно возникает обратный вопрос – каждой ли данной матрице 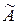при заданном базисе в V можно поставить в соответствие линейный оператор А, матрицей которого будет данная матрица. Важно также выяснить вопрос о единственности матрицы линейного оператора в заданном базисе.

Теорема 1.6 Пусть в линейном пространстве V задан базис 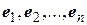, и пусть – квадратная матрица, содержащая строк и столбцов. Существует единственный линейный оператор А, матрицей которого в заданном базисе является матрица .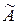

Замечание 3 Пусть А и В – квадратные матрицы порядка , А и В – отвечающие им линейные операторы в заданном базисе 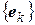пространства V. Из доказательства теоремы 1.6 следует, что матрице 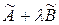, где λ – некоторое число, отвечает линейный оператор 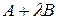(напомним, что А, В и 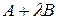принадлежат ).

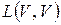Теорема 1.7 Ранг линейного оператора А равен рангу матрицы 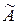этого оператора: .

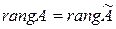Пример Оператор переводит вектор 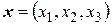в вектор 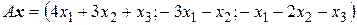. Является ли оператор А линейным? Если да, то найти его ранг дефект, образ и ядро.

Решение. Несложно проверить, что заданный оператор является линейным.

Запишем матрицу этого оператора, для чего найдем образы базисных векторов , , :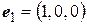

, , .

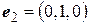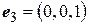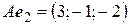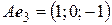Будем иметь: 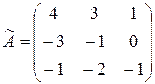. Согласно теореме 1.7 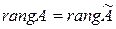, поэтому 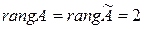(ранг матрицы найти любым способом). Используя утверждение теоремы 1.2, получим .

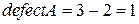Найдем векторы, принадлежащие ядру: 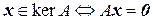или в матричной форме: 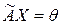. Таким образом, имеем однородную систему линейных алгебраических уравнений, фундаментальным решением которой будет вектор 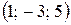, т.е. .

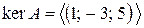Найдем векторы, принадлежащие образу: 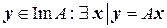или в матричной форме: 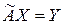. Полученная система линейных алгебраических уравнений должна иметь решение. Исследовав ее на совместность, результатом чего будет однородная система линейных алгебраических уравнений относительно переменных , получим фундаментальное решение: , , 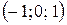т.е. .

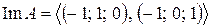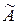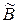Пусть и – произвольные квадратные матрицы, содержащие строк и столбцов. Из теорем 1.4, 1.5, 1.6 и 1.7 вытекают следующие следствия.

Следствие 1 Ранг произведения 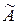и 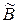удовлетворяет соотношениям

, , .

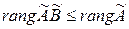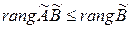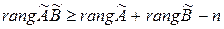Следствие 2 Обратный оператор 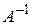для оператора А существует только тогда, когда ранг матрицы 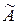оператора А равен , т.е. размерности пространства. Отметим, что в этом случае существует также и обратная матрица 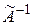для матрицы .

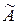1.3 Преобразование матрицы линейного оператора при переходе к новому базису

Пусть V – линейное пространство, А – линейный оператор из 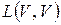, 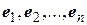и – два базиса в V и

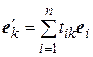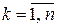, (1.16)

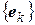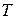– формулы перехода от базиса к базису . Обозначим через матрицу :

. (1.17)

Отметим, что 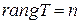. Пусть

и (1.18)

– матрицы оператора А в указанных базисах. Найдем связь между этими матрицами.

Справедливо следующее утверждение.

Теорема 1.8 Матрицы 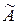и 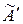оператора А в базисах 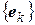и соответственно связаны соотношением

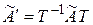, (1.19)

где 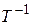– обратная матрица для матрицы 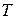, определенной равенством (1.17).

Пример Могут ли матрицы 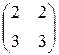и 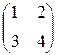быть матрицами одного линейного оператора в разных базисах?

Матрица перехода должна быть невырожденной, поэтому обе матрицы должны быть невырожденными. Будем иметь

, .

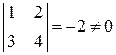Значит, указанные матрицы не могут быть матрицами одного линейного оператора в разных базисах.

Пример Дана матрица линейного оператора в базисе 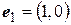, 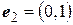. Найти матрицу этого линейного оператора в базисе , .

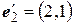Запишем матрицу перехода, найдем к ней обратную:

, .

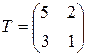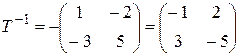Вычислим матрицу 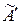по формуле (1.19):

.

Замечание 1 Обратимся к формуле 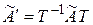. Умножая обе части этого матричного равенства слева на матрицу 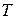и справа на 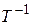, получим соотношение

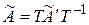, (1.20)

представляющее собой другую форму связи между матрицам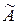и и 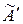линейного оператора А в разных базисах.

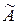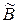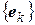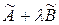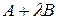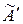Замечание 2 Пусть и – квадратные матрицы порядка , А и В – отвечающие им линейные операторы в заданном базисе . Как уже отмечалось (см. замечание 3 предыдущего пункта) матрице отвечает линейный оператор . Выясним вид матрицы этого оператора в базисе . Пусть и 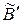– матрицы операторов А и В в базисе . Тогда, согласно (1.19), имеем

, .

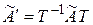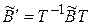Матрица линейного оператора 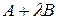в базисе имеет, согласно (1.19), следующий вид: .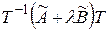

Следствие из теоремы 1.8 .

1.4 Собственные значения и собственные векторы линейных операторов

Пусть А – линейный оператор, а I – тождественный оператор из .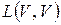

Число λ называется собственным значением (числом) оператора А, если существует ненулевой вектор такой, что

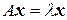. (1.23)

При этом вектор называется собственным вектором оператора А, отвечающим собственному значению λ.

Множество всех собственных значений оператора A называется его спектром и обозначается .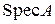

Многочлен относительно λ

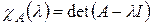(1.24)

называется характеристическим многочленом оператора А, а уравнение

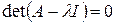(1.25)

называется характеристическим.

Теорема 1.9 Для того чтобы число λ было собственным значением оператора А, необходимо и достаточно, чтобы это число было корнем характеристического уравнения (1.25) оператора А.

Следствие. Каждый линейный оператор имеет собственное значение.

Замечание 1 Так как значение определителя 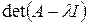не зависит от выбора базиса, то коэффициенты характеристического многочлена в правой части (1.25) также не зависят от выбора базиса. Таким образом, коэффициенты характеристического многочлена оператора А представляют собой инварианты – величины, значения которых не зависят от выбора базиса.

В частности, коэффициент, равный , является инвариантом. Этот инвариант называется следом оператора А и обозначается символом :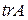

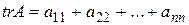. (1.27)

Алгебраической кратностью собственного значения λ называется кратность корня λ характеристического многочлена .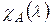

Пусть теперь λ – собственное значение линейного оператора A. Тогда, по определению, ненулевой вектор будет собственным, если 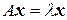или, что равносильно, . Отсюда получаем, что подпространство 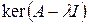состоит из всех собственных векторов, отвечающих собственному значению λ, и нулевого вектора. Это подпространство называется собственным. Его размерность называется геометрической кратностью собственного значения λ. Таким образом, для нахождения геометрической кратности собственного значения λ нужно найти размерность ядра линейного оператора 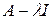. Часто удобнее находить равную последней размерность подпространства решений однородной системы уравнений 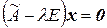. Если найдена фундаментальная система решений этой однородной системы уравнений (заметим, что фундаментальная система решений состоит из собственных векторов), то число векторов в ней равно геометрической кратности собственного значения λ. Однако, находить специально фундаментальную систему решений нерационально, так как размерность подпространства решений однородной системы уравнений 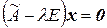, а, следовательно, и геометрическая кратность собственного значения λ, равна 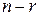, где число 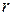равно рангу матрицы 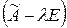. Очевидно, что алгебраическая и геометрическая кратности собственного значения больше нуля и не превосходят размерности линейного пространства. Кроме того, геометрическая кратность собственного значения не превосходит его алгебраической кратности.

Все введенные понятия (собственное значение, собственный вектор, спектр, характеристический многочлен) переносятся с линейного оператора на его матрицу. Отметим также, что определение собственного значения и собственного вектора для операторов, действующих в бесконечномерных линейных пространствах, остается таким же, как и в конечномерном случае. Однако спектр линейного оператора в бесконечномерном случае определяется несколько иначе. Он включает в себя все собственные значения, но может содержать и другие значения.

Теорема 1.10 Геометрическая кратность λ не превосходит алгебраической.

Пример Найти собственные значения и собственные векторы линейного оператора, заданного матрицей .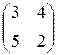

Решение. Составим характеристическое уравнение и найдем его корни (собственные значения):

.

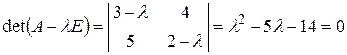Собственные значения: , 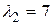. Найдем собственные векторы.

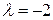. Тогда

.

Решая систему, получим

Тогда, собственный вектор, соответствующий собственному значению 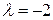, будет .

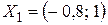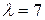. Тогда

.

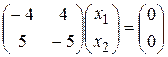Решая систему, получим

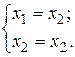
Тогда, собственный вектор, соответствующий собственному значению 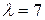, будет .

Теорема 1 .11 Для того чтобы матрица 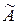линейного оператора А в данном базисе была диагональной, необходимо и достаточно, чтобы базисные векторы 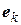были собственными векторами этого оператора. Линейные операторы, имеющие в некотором базисе диагональную матрицу, называются операторами простой структуры.

Date: 2015-08-24; view: 1448; Нарушение авторских прав