Тема 4. Інтегрування диференціального рівнянь руху матеріальної точки, на яку діє сила, що залежить від координати

Диференціальне рівняння руху точки в цьому випадку має вигляд

. (1)

з початковими умовами: при 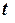= 0: , .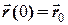

Якщо сила залежить лише від положення точки, то кожна декартова проекція сили залежить лише від відповідної проекції радіус-вектора, і рівняння (1) розкладається на три скалярні. В випадку одномірного руху точки диференціальне рівняння, наприклад, для 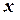- компоненти має вигляд

. (2)

Далі для спрощення записів будемо опускати індекси. Безпосередньо розділити змінні в такому рівнянні не вдається, тому виконаємо наступні перетворення

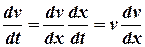. (3)

Тоді, після розділу змінних, диференціальне рівняння приймає вигляд

, (4)

звідки, після інтегрування, отримуємо 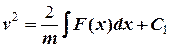, або

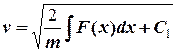. (5)

Враховуючи що 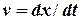, з (5) отримуємо

. (6)

Проводячи повторне інтегрування, знаходимо

. (7)

(Зауважимо, що в загальному випадку в рівнянні (7) виникають складні інтеграли, але в випадках, коли 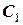= 0, інтегрування не викликає труднощів.)

Розв’язуючи рівняння (7) відносно координати 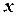, знайдемо її залежність від часу та постійних інтегрування

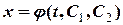. (8)

Date: 2015-08-15; view: 371; Нарушение авторских прав