Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задача ДТ.2. Інтегрування диференціального рівняння руху матеріальної точки, на яку діє сила тяжіння
|
|
Знайти закон руху тіла масою m (кг), що почало рухатись в полі тяжіння Землі зі швидкістю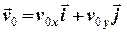 
(м/с) з точки 
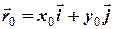(м). Визначити координати та швидкість тіла, тангенціальну та нормальну сили і радіус кривизни траєкторії у заданий момент часу 
(с). Опором повітря знехтувати, прискорення вільного падіння вважати 9,8 м/с2. Всі вектори зобразити на малюнку у зручному масштабі. Дані приведені у таблиці 2.
Таблиця 2
Вихідні дані для виконання задачі ДТ.2
| № | m | 
| 
| 
| 
|
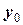
| № | m |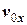
|
|
| 
|
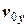
| № | m |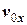
|
|
|
|
|
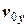
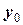
| 0,5 | * | 3,0 | 0,5 | ** | ||||||||||||||||
| 2,0 | 4,0 | 5,0 | ||||||||||||||||||
| 3,0 | 2,0 | * | 4,0 | * | ||||||||||||||||
| 4,0 | 4,0 | 3,0 | ||||||||||||||||||
| 4,0 | ** | 0,5 | ** | 2,0 | ** | |||||||||||||||
| 0,5 | 4,0 | 4,0 | ||||||||||||||||||
| 3,0 | 0,5 | * | 5,0 | |||||||||||||||||
| 4,0 | 3,0 | 3,0 | ||||||||||||||||||
| 2,0 | 0,5 | 0,5 | ||||||||||||||||||
| 4,0 | 5,0 | * | 5,0 | * |
* в найвищій точці траєкторії;
** в момент падіння на Землю.
Приклад. Знайти для початкових умов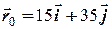 
, 
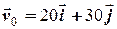координати та швидкість тіла, нормальне та тангенціальне прискорення і радіус кривизни траєкторії в момент часу 
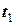= 1 с. Прискорення вільного падіння вважати рівним 9,8 м/с2.
Розв’язок. Дані початкові умови визначають конкретний вигляд рівнянь руху тіла в полі тяжіння Землі Скористаємося отриманими формулами (13) та (14), які згідно умовам задачі приймають вид:
,
.
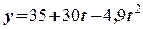Підставляючи час 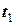= 1 с, отримаємо координати тіла:
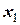= 35 (м), 
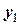= 60,1 (м).
Згідно формули (8) горизонтальна компонента швидкості не змінюється
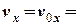20 (м/с),
а вертикальна компонента швидкості змінюється за законом (6)
(м/с),
що для 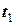= 1 с дає 
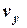= 20,2 (м/с).
Модуль швидкості та її напрям знайдемо, скориставшись формулами (6) та (8):
= 28,4 (м/с),
tg 
= 
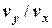
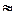1,
отже,
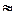45°.
Знаючи кут, який утворює швидкість з горизонтом, модуль тангенціального прискорення знайдемо, як проекцію прискорення вільного падіння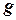 
на вектор швидкості
= 6,9 (м/с2).
(Зауважимо, що тангенціальне прискорення може бути знайдено за формулою, яка відома з кінематики
,
що дає той самий результат.)
Тоді для нормального прискорення маємо
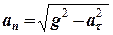= 6,9 (м/с2).
Оскільки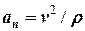 
, то для радіуса кривизни траєкторії отримуємо
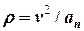= 117 (м).
Відповідь: 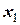= 35 м, 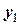= 60,1 м, 
= 28,4 м/с,
= 
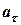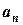= 6,9 м/с2, 
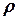= 117 м.
Date: 2015-08-15; view: 404; Нарушение авторских прав