
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача ДТ.3. Інтегрування диференціального рівняння руху матеріальної точки, на яку діють сталі сили
|
|
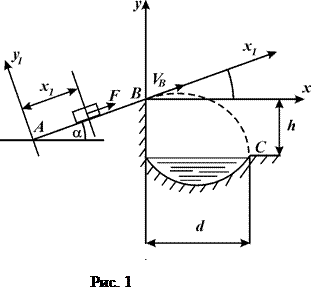 Варіанти 1, 4, 7, 10, 13, 16, 19, 22, 25, 28: Мотоцикл під дією сталої сили
Варіанти 1, 4, 7, 10, 13, 16, 19, 22, 25, 28: Мотоцикл під дією сталої сили 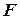 піднімається
піднімається  с по ділянці
с по ділянці 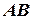 довжиною
довжиною 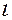 , яка складає з горизонтом кут
, яка складає з горизонтом кут  (рис. 1). Мотоцикл має в точці
(рис. 1). Мотоцикл має в точці 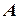 швидкість
швидкість 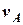 . В точці
. В точці  він досягає швидкості
він досягає швидкості 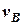 , перелітає через рів шириною
, перелітає через рів шириною 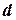 і через
і через 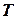 с приземляється в точці
с приземляється в точці 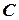 , маючи швидкість
, маючи швидкість  . Маса мотоцикла з мотоциклістом
. Маса мотоцикла з мотоциклістом 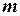 . При розв’язку задачі мотоцикл з мотоциклістом вважати матеріальною точкою, нехтувати тертям кочення та силою опору повітря.
. При розв’язку задачі мотоцикл з мотоциклістом вважати матеріальною точкою, нехтувати тертям кочення та силою опору повітря.
Варіант № 1. Дано:  = 30°;
= 30°; 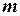 = 400 кг,
= 400 кг, 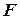 = 2,2 кН;
= 2,2 кН;  = 0;
= 0;  = 40 м;
= 40 м;
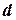 = 5 м. Знайти
= 5 м. Знайти 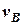 та
та 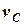 .
.
Варіант № 4. Дано:  = 30°;
= 30°; 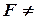 0;
0;  = 40 м;
= 40 м;  = 0;
= 0; 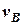 = 4,5 м/с;
= 4,5 м/с;
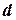 = 3 м. Знайти
= 3 м. Знайти  та
та  .
.
Варіант № 7. Дано:  = 30°;
= 30°;  = 0;
= 0; 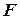 = 2 кН;
= 2 кН;  = 50 м;
= 50 м;  = 2 м;
= 2 м; 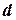 = 4 м. Знайти
= 4 м. Знайти 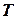 та
та 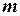 .
.
Варіант № 10. Дано:  = 30°;
= 30°; 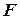 = 0;
= 0;  = 40 м;
= 40 м; 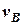 = 4,5 м/с;
= 4,5 м/с;  = 2,5 м. Знайти
= 2,5 м. Знайти  та
та 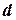 .
.
Варіант № 13. Дано:  = 30°;
= 30°; 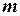 = 400 кг,
= 400 кг,  = 0;
= 0;  = 20 с;
= 20 с; 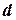 =3 м;
=3 м;
 = 1,5 м. Знайти
= 1,5 м. Знайти 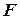 та
та  .
.
Варіант № 16. Дано:  = 30°;
= 30°; 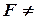 0;
0;  = 40 м;
= 40 м;  = 0;
= 0; 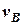 = 4,5 м/с;
= 4,5 м/с;
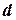 = 3 м. Знайти
= 3 м. Знайти  та
та  .
.
Варіант № 19. Дано:  = 30°;
= 30°; 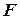 = 0;
= 0;  = 45 м;
= 45 м; 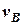 = 5,5 м/с;
= 5,5 м/с;  = 2,0 м. Знайти
= 2,0 м. Знайти  та
та 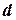 .
.
Варіант № 22. Дано:  = 30°;
= 30°; 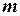 = 400 кг,
= 400 кг,  = 0;
= 0;  = 20 с;
= 20 с; 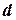 = 3 м;
= 3 м;
 = 1,5 м. Знайти
= 1,5 м. Знайти 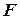 та
та  .
.
Варіант № 25. Дано:  = 30°;
= 30°; 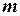 = 350 кг,
= 350 кг, 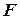 = 2,0 кН;
= 2,0 кН;  = 0;
= 0;  = 45 м;
= 45 м;
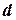 = 7 м. Знайти
= 7 м. Знайти 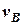 та
та 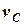 .
.
Варіант № 28. Дано:  = 30°;
= 30°;  = 0;
= 0; 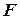 = 2,4 кН;
= 2,4 кН;  = 50 м;
= 50 м;  =3 м;
=3 м;
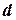 = 5 м. Знайти
= 5 м. Знайти 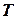 та
та 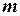 .
.
Варіанти 2, 5, 8, 11, 14, 17, 20, 23, 26, 29: Тіло рухається з точки 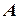 по ділянці
по ділянці 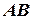 довжиною
довжиною 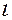 , яка складає з горизонтом кут
, яка складає з горизонтом кут  . Його початкова швидкість
. Його початкова швидкість 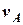 , а коефіцієнт тертя ковзання на ділянці
, а коефіцієнт тертя ковзання на ділянці 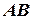 дорівнює
дорівнює  (рис. 2). Через
(рис. 2). Через 
 с в точці
с в точці  воно покидає похилу площину зі швидкістю
воно покидає похилу площину зі швидкістю 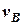 і падає на горизонтальну площину в точці
і падає на горизонтальну площину в точці 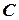 , маючи швидкість
, маючи швидкість  , перебуваючи в повітрі
, перебуваючи в повітрі 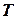 с.
с.
При розв’язку задачі тіло вважати матеріальною точкою масою 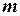 та нехтувати силою опору повітря.
та нехтувати силою опору повітря.
Варіант № 2. Дано:  = 0;
= 0;
 = 30°;
= 30°;  = 0,2;
= 0,2;  = 6 м;
= 6 м;  = 4,5 м. Знайти
= 4,5 м. Знайти 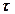 та
та 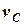 .
.
Варіант № 5. Дано:  = 30°;
= 30°;
 = 0,1;
= 0,1;  = 1 м/с;
= 1 м/с;  = 1,5 с;
= 1,5 с;  = 10 м. Знайти
= 10 м. Знайти 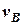 та
та 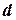 .
.
Варіант № 8. Дано:  = 0;
= 0;  = 0;
= 0;  = 9,81 м;
= 9,81 м;  = 2 с;
= 2 с;  = 20 м. Знайти
= 20 м. Знайти  та
та 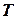 .
.
Варіант № 11. Дано:  = 0;
= 0;  = 45°;
= 45°;  = 10 м;
= 10 м;  = 2 с. Знайти
= 2 с. Знайти  та рівняння траєкторії на ділянці
та рівняння траєкторії на ділянці 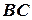 .
.
Варіант № 14. Дано:  = 0;
= 0;  = 30°;
= 30°;  = 0,2;
= 0,2;  = 10 м;
= 10 м; 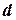 = 12 м. Знайти
= 12 м. Знайти 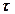 та
та 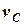
Варіант № 17. Дано:  = 30°;
= 30°;  = 0,15;
= 0,15;  = 1,5 м/с;
= 1,5 м/с;  = 2,0 с;
= 2,0 с;  = 12 м. Знайти
= 12 м. Знайти 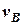 та
та 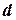 .
.
Варіант № 20. Дано:  = 0;
= 0;  = 45°;
= 45°;  = 10 м;
= 10 м;  = 2 с. Знайти
= 2 с. Знайти  та рівняння траєкторії на ділянці
та рівняння траєкторії на ділянці 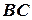 .
.
Варіант № 23. Дано:  = 0;
= 0;  = 0;
= 0;  = 5,5 м;
= 5,5 м;  = 1,5 с;
= 1,5 с;  = 20 м. Знайти
= 20 м. Знайти  та
та 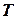 .
.
Варіант № 26. Дано:  = 0;
= 0;  = 30°;
= 30°;  = 0,2;
= 0,2;  = 10 м;
= 10 м; 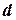 = 12 м. Знайти
= 12 м. Знайти 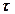 та
та 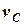
Варіант № 29. Дано:  = 0;
= 0;  = 30°;
= 30°;  = 0,15;
= 0,15;  = 6 м;
= 6 м;  = 5,5 м. Знайти
= 5,5 м. Знайти 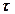 та
та 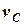 .
.
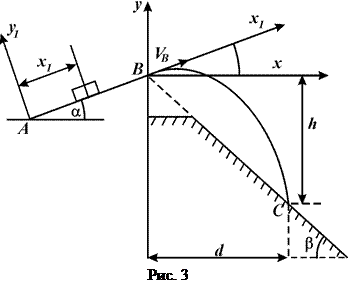
Варіанти 3, 6, 9, 12, 15, 18, 21, 24, 27, 30: Лижник підходить до точки 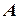 трампліна
трампліна 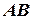 довжиною
довжиною 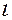 , який складає з горизонтом кут
, який складає з горизонтом кут  , зі швидкістю
, зі швидкістю 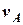 (рис. 3). Коефіцієнт тертя ковзання на ділянці
(рис. 3). Коефіцієнт тертя ковзання на ділянці 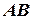 дорівнює
дорівнює  . Лижник від
. Лижник від 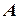 до
до  рухається
рухається  с і в точці
с і в точці  зі швидкістю
зі швидкістю 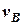 він покидає трамплін. Через
він покидає трамплін. Через 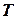 с лижник приземляється зі швидкість
с лижник приземляється зі швидкість  в точці
в точці 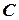 гори, яка складає кут
гори, яка складає кут  з горизонтом.
з горизонтом.
 Варіант № 3. Дано:
Варіант № 3. Дано:  = 20°;
= 20°;  = 0,1;
= 0,1;  = 16 м/с;
= 16 м/с;  = 5 м;
= 5 м;
 = 60°. Знайти
= 60°. Знайти 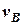 та
та 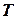
Варіант № 6. Дано:  = 15°;
= 15°;  = 0,15;
= 0,15;  = 0,2 с;
= 0,2 с;  = 40 м;
= 40 м;
 = 30°. Знайти
= 30°. Знайти 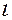 та
та 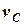 .
.
Варіант № 9. Дано:  = 18 м/с;
= 18 м/с;  = 0;
= 0; 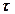 = 0,3 с;
= 0,3 с; 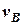 = 15 м/с;
= 15 м/с;  = 60°. Знайти
= 60°. Знайти  та
та 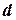 .
.
Варіант № 12. Дано:  = 15°;
= 15°;  = 0;
= 0;  = 12 м/с;
= 12 м/с; 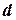 = 50 м;
= 50 м;
 = 60°. Знайти
= 60°. Знайти 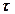 та рівняння траєкторії лижника на ділянці
та рівняння траєкторії лижника на ділянці 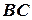 .
.
Варіант № 15. Дано:  = 15°;
= 15°; 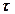 = т0,3 с;
= т0,3 с;  = 0,1;
= 0,1; 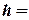 42 м;
42 м;  =45°. Знайти
=45°. Знайти 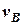 та
та  .
.
Варіант № 18. Дано:  = 20°;
= 20°;  = 0,1;
= 0,1;  = 0,2 с;
= 0,2 с;  = 40 м;
= 40 м;  = 30°. Знайти
= 30°. Знайти 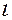 та
та 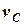 .
.
Варіант № 21. Дано:  = 15°;
= 15°;  = 0,1;
= 0,1;  = 16 м/с;
= 16 м/с;  = 5 м;
= 5 м;  = 45°. Знайти
= 45°. Знайти 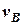 та
та 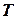 .
.
Варіант № 24. Дано:  = 21 м/с;
= 21 м/с;  = 0;
= 0; 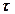 = 0,3 с;
= 0,3 с; 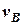 = 20 м/с;
= 20 м/с;  = 60°. Знайти
= 60°. Знайти  та
та 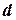 .
.
Варіант № 27. Дано:  = 15°;
= 15°; 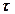 = 0,3 с;
= 0,3 с;  = 0,1;
= 0,1;  м;
м;  = 30°. Знайти
= 30°. Знайти 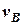 та
та  .
.
Варіант № 30. Дано:  =15°;
=15°;  = 0;
= 0;  = 12 м/с;
= 12 м/с; 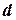 = 50 м;
= 50 м;  = 60°. Знайти
= 60°. Знайти 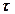 та рівняння траєкторії лижника на ділянці
та рівняння траєкторії лижника на ділянці 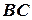 .
.
Приклад. Тіло рухається з точки 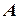 похилої площини маючи початкову швидкість
похилої площини маючи початкову швидкість 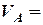 12 м/с. Коефіцієнт тертя ковзання
12 м/с. Коефіцієнт тертя ковзання  0,1, кут нахилу площини до горизонту
0,1, кут нахилу площини до горизонту 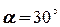 . Через
. Через 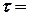 0,5 с тіло покидає похилу площину і падає на горизонтальну площину в точці
0,5 с тіло покидає похилу площину і падає на горизонтальну площину в точці 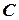 (рис. 4).
(рис. 4).
Визначити довжину 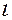 похилої площини, швидкість точки
похилої площини, швидкість точки 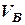 в кінці похилої площини, а також координати (
в кінці похилої площини, а також координати ( ) точки падіння, швидкість тіла в момент падіння
) точки падіння, швидкість тіла в момент падіння  тіла на горизонтальну площину, та кут падіння.
тіла на горизонтальну площину, та кут падіння.
Розв’язок. Розглянемо рух тіла по похилій площині. Приймаємо тіло за матеріальну точку, на яку діють сили: вага 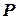 , нормальнареакція N та сила тертя ковзання
, нормальнареакція N та сила тертя ковзання 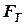 . Рівняння руху точки має вид
. Рівняння руху точки має вид
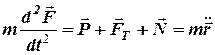 . (1)
. (1)
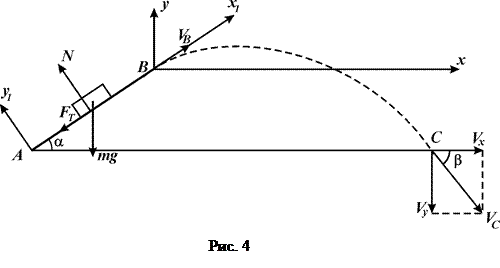 |
Розташуємо початок декартової системи координат

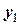 в точці
в точці 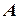 , спрямувавши вісь
, спрямувавши вісь  вздовж площини
вздовж площини 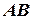 (рис. 4), і отримуємо відповідні скалярні рівняння для сил, що діють вздовж цих напрямів:
(рис. 4), і отримуємо відповідні скалярні рівняння для сил, що діють вздовж цих напрямів:
 , (2)
, (2)
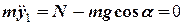 , (3)
, (3)
отже 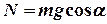 .
.
Оскільки  , перепишемо (2) в наступному вигляді
, перепишемо (2) в наступному вигляді
 ,
,
де 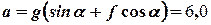 м/с.
м/с.
Інтегруючи двічі останнє диференційне рівняння, отримуємо:
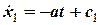 ,
,
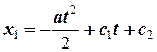 .
.
Для визначення сталих інтегрування  , та
, та 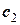 скористаємося початковими умовами:
скористаємося початковими умовами: 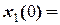 0,
0,  , і отримуємо:
, і отримуємо:
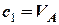 ,
, 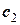 = 0,
= 0,
Тоді, остаточно, для координати тіла  та його швидкості
та його швидкості  на першому етапі руху маємо:
на першому етапі руху маємо:
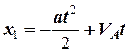 , (4)
, (4)
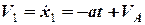 . (5)
. (5)
Ці рівняння дозволяють визначити швидкість тіла в момент часу  , коли тіло покидає похилу площину та довжину похилої площини:
, коли тіло покидає похилу площину та довжину похилої площини:
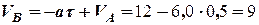 (м/с), (6)
(м/с), (6)
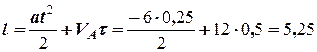 (м). (7)
(м). (7)
Далі розглянемо рух тіла від точки  до точки падіння
до точки падіння 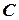 . На цій ділянці діє лише сила тяжіння
. На цій ділянці діє лише сила тяжіння 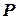 тому диференціальне рівняння руху має вид
тому диференціальне рівняння руху має вид
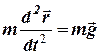 .
.
Розташуємо початок нової декартової системи координат 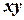 в точці
в точці  (рис. 4), спрямувавши вісі відповідно горизонтально та вертикально вгору, і тоді отримуємо наступні диференціальні рівняння руху на другій ділянці руху:
(рис. 4), спрямувавши вісі відповідно горизонтально та вертикально вгору, і тоді отримуємо наступні диференціальні рівняння руху на другій ділянці руху:
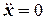 ,
, 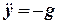 . (8)
. (8)
Початкові умови на цій ділянці наступні:
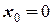 ,
, 
 7,8 (м/с),
7,8 (м/с),
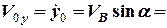 4,5 (м/с).
4,5 (м/с).
Двічі інтегруємо диференціальні рівняння (8) і послідовно отримаємо:
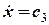 ,
, 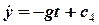
 ,
,
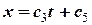 ,
,  .
.
Запишемо отримані рівняння для моменту часу 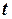 = 0:
= 0:
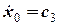 ,
, 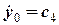 ,
,
 ,
, 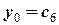 ,
,
і знайдемо з них сталі інтегрування:
 ,
,
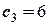 (м/с),
(м/с), 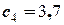 ( м/с).
( м/с).
Таким чином, рівняння для визначення координат та компонентшвидкості на другої ділянці руху набувають вигляду:
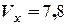 ( м/с ),
( м/с ), 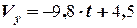 ( м/с),
( м/с),
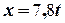 (м),
(м), 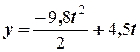 (м).
(м).
Точка падіння тіла на площину (дивись рис. 1) має координату
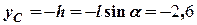 (м),
(м),
що дозволяє записати рівняння для визначення часу руху тіла та ділянці 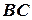
 ,
,
розв’язок якого дає 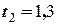 с.
с.
Цей час дозволяє визначити 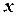 - координату точці падіння тіла
- координату точці падіння тіла
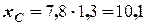 (м),
(м),
компоненти швидкості:
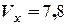 (м/с),
(м/с),  (м/с),
(м/с),
і також модуль швидкості в точці падіння
 (м/с).
(м/с).
Кут  з горизонтом (під яким тіло падає на площину) знайдемо з геометричних міркувань (дивись рис. 4)
з горизонтом (під яким тіло падає на площину) знайдемо з геометричних міркувань (дивись рис. 4)
 ,
,
що дає 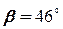 .
.
Відповідь: 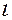 = 5,25 м,
= 5,25 м,  м/с,
м/с, 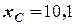 м,
м, 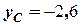 м,
м, 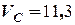 м/с,
м/с, 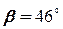
Date: 2015-08-15; view: 686; Нарушение авторских прав