
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 2. Інтегрування диференціального рівнянь руху матеріальної точки, яка знаходиться під дією сталих сил
|
|
Розв’яжемо обернену задачу динаміки матеріальної точки в найпростішому випадку, коли сила 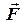 є величиною сталою, (не залежить від
є величиною сталою, (не залежить від 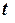 ,
, 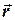 та
та  ). (Ця задача дійсно має зміст, бо, наприклад, відповідає задачі про рух тіла, кинутого під кутом до горизонту, якщо нехтувати опором повітря, а параметри траєкторії значно менші за радіус Землі – в таких умовах можна розглядати тіло як матеріальну точку, а поле тяжіння Землі - однорідним.)
). (Ця задача дійсно має зміст, бо, наприклад, відповідає задачі про рух тіла, кинутого під кутом до горизонту, якщо нехтувати опором повітря, а параметри траєкторії значно менші за радіус Землі – в таких умовах можна розглядати тіло як матеріальну точку, а поле тяжіння Землі - однорідним.)
Якщо 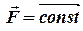 ми у змозі обрати одну з декартових осей паралельно лінії дії сили, тоді проекції сили на дві інші осі залишаться рівними нулю. Скористаємось цією обставиною для розв’язку задачі про рух тіла кинутого під кутом до горизонту в однорідному полі тяжіння Землі, нехтуючи опором повітря. В цьому випадку на тіло діє лише одна сила тяжіння
ми у змозі обрати одну з декартових осей паралельно лінії дії сили, тоді проекції сили на дві інші осі залишаться рівними нулю. Скористаємось цією обставиною для розв’язку задачі про рух тіла кинутого під кутом до горизонту в однорідному полі тяжіння Землі, нехтуючи опором повітря. В цьому випадку на тіло діє лише одна сила тяжіння  , тому диференціальне рівняння руху має вигляд
, тому диференціальне рівняння руху має вигляд
 . (1)
. (1)
Спрямуємо вісь 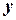 вертикально вгору, а вісі
вертикально вгору, а вісі 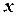 та
та 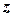 - лежать у горизонтальній площині.
- лежать у горизонтальній площині.
У цьому випадку рівняння (1) може бути записано в вигляді
 , (2)
, (2)
де 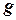 - прискорення вільного падіння.
- прискорення вільного падіння.
Рівняння (2) необхідно доповнити початковими умовами - при 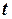 = 0:
= 0:
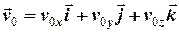 , (3)
, (3)
 . (4)
. (4)
Шість величин  ,
, 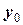 ,
,  та
та  ,
,  ,
, 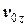 дозволять нам визначити сталі інтегрування диференціального рівняння (2).
дозволять нам визначити сталі інтегрування диференціального рівняння (2).
Розглянемо 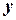 - компоненту рівняння (2) і перепишемо його у вигляді
- компоненту рівняння (2) і перепишемо його у вигляді
 . (5)
. (5)
Розділення змінних цього рівняння і відповідне інтегрування дозволяє отримати
 .
.
З врахуванням початкових умов визначаємо 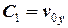 , отже
, отже
 . (6)
. (6)
Оскільки 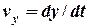 , то з рівняння (6) отримуємо
, то з рівняння (6) отримуємо
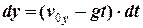 .
.
Інтегруючи останній вираз, отримуємо
 ,
,
а сталу визначаємо з початкових умов  . Отже отримуємо закон руху тіла вздовж осі
. Отже отримуємо закон руху тіла вздовж осі 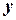
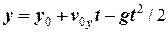 . (7)
. (7)
Що стосується руху тіла вздовж осей 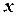 та
та 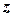 , то з урахуванням того, що:
, то з урахуванням того, що:
 , та
, та  ,
,
перше інтегрування цих рівнянь приведе до визначення сталих швидкостей:
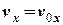 , (8)
, (8)
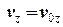 , (9)
, (9)
а повторне інтегрування дає закони рівномірного руху вздовж цих осей:
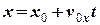 , (10)
, (10)
 . (11)
. (11)
Рівняння (10) та (11) дозволяють визначити траєкторію руху в горизонтальній площині  . Якщо виключити час з системи цих рівнянь, то ми отримаємо рівняння прямої лінії у вигляді
. Якщо виключити час з системи цих рівнянь, то ми отримаємо рівняння прямої лінії у вигляді
 (12)
(12)
Вздовж цієї прямої, яка лежить в горизонтальній площині, відбувається зміна горизонтальної координати, при цьому швидкість зміни координати буде сталою  - доведіть це самостійно.
- доведіть це самостійно.
Таким чином, ми довели, що траєкторія руху тіла в однорідному полі тяжіння є плоскою. Тому, при розв’язку таких задач одну з осей системи відліку (наприклад, вісь 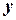 ), напрямляють вздовж лінії дії сили, а іншу (наприклад, вісь
), напрямляють вздовж лінії дії сили, а іншу (наприклад, вісь 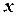 ) – вздовж проекції початкової швидкості на площину, що перпендикулярна до сталої сили (дивись наступний приклад). Тоді у всіх отриманих формулах можемо покласти
) – вздовж проекції початкової швидкості на площину, що перпендикулярна до сталої сили (дивись наступний приклад). Тоді у всіх отриманих формулах можемо покласти 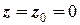 та
та  і отримати наступні закон руху тіла у параметричній формі:
і отримати наступні закон руху тіла у параметричній формі:
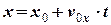 , (13)
, (13)
 . (14)
. (14)
Date: 2015-08-15; view: 524; Нарушение авторских прав