
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

А) Вільні (власні) коливання з одним ступенем свободи
|
|
Малі коливання, які здійснює матеріальна точка масою m під дією лише квазіупружної сили 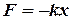 називаються вільними незатухаючими. Такі одномірні коливання, наприклад, вздовж осі x, описуються диференціальним рівнянням
називаються вільними незатухаючими. Такі одномірні коливання, наприклад, вздовж осі x, описуються диференціальним рівнянням
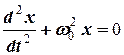 , (1)
, (1)
з початковими умовами:
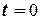 :
: 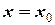 та
та 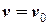 .
.
Тут: 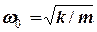 - кругова частота коливань,
- кругова частота коливань,  - жорсткість пружини, а відлік осі x починається в точці x = 0.
- жорсткість пружини, а відлік осі x починається в точці x = 0.
Для розв’язку однорідного диференціального рівняння (1) зі сталими коефіцієнтами потрібно скласти характеристичне рівняння:
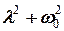 = 0. (2)
= 0. (2)
Корені цього рівняння будуть чисто уявними ( ), тому загальний розв’язок рівняння (1) після перетворень Ейлера буде мати вид
), тому загальний розв’язок рівняння (1) після перетворень Ейлера буде мати вид
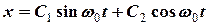 . (3)
. (3)
Частіше записують розв’язок через одну гармонічну функцію
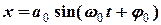 . (4)
. (4)
Сталі інтегрування 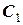 та
та 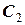 (чи
(чи 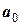 та
та 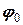 ) знаходять з початкових умов. Наприклад так: спочатку визначимо швидкість тіла як похідну від зміщення
) знаходять з початкових умов. Наприклад так: спочатку визначимо швидкість тіла як похідну від зміщення
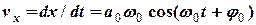 , (5)
, (5)
а потім підставимо початкові умови в (4) та (5):
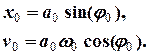 (6)
(6)
Якщо піднести ці вирази до другого ступеня та скласти, то можна отримати вираз для амплітуди, а якщо поділити – то вираз для початкової фази:
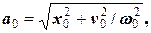 (7)
(7)
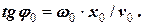 (8)
(8)
Коливання, які здійснюються за законом (3) чи (4) називаються гармонічними, але закон (4) аналізувати значно легше, ніж (3). Величина 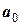 вказує найбільше відхилення точки від положення рівноваги і називається амплітудою коливань, величина
вказує найбільше відхилення точки від положення рівноваги і називається амплітудою коливань, величина 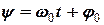 - фазою коливань, а
- фазою коливань, а 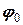 - початковою фазою коливань.
- початковою фазою коливань.
Зауважимо, що частота вільних коливань ( ) не залежить від дії на тіло сталої сили.
) не залежить від дії на тіло сталої сили.
Контрольні запитання
1. Сформулюйте умови виникнення коливань.
2. Як спрямована сила, що викликає гармонічні коливання? Чи існують в природі такі сили?
3. Запишіть диференціальне рівняння коливального руху. Що необхідно знати для однозначного розв’язку такого рівняння?
4. Як отримати розв’язок такого рівняння?
5. Запишіть розв’язок диференціального рівняння коливального руху. Що таке період та амплітуда коливань?
6. Від чого залежить період (частота) коливань та амплітуда коливань?
7. Як впливає стала сила, що діє на матеріальну точку, на її коливання?
Приклад 1. Тіло масою 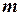 = 0,5 кг закріплено до двох недеформованих пружинах жорсткістю
= 0,5 кг закріплено до двох недеформованих пружинах жорсткістю 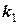 = 60 Н/м та
= 60 Н/м та 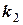 = 140 Н/м (рис. 16). Точка закріплення діліть відстань між пружинами у відношенні обернено пропорційно жорсткостям пружин. Знайти положення рівноваги, відносно якого мають місце коливання. 2) Записати диференціальне рівняння вільних незатухаючих коливань та розв’язати його для початкових умов
= 140 Н/м (рис. 16). Точка закріплення діліть відстань між пружинами у відношенні обернено пропорційно жорсткостям пружин. Знайти положення рівноваги, відносно якого мають місце коливання. 2) Записати диференціальне рівняння вільних незатухаючих коливань та розв’язати його для початкових умов 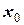 = 0,1 м,
= 0,1 м, 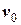 = - 2,0 м/с. Визначити початкову фазу
= - 2,0 м/с. Визначити початкову фазу 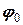 , частоту
, частоту  , амплітуду
, амплітуду 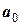 таких коливань.
таких коливань.
 Розв’язок. Перш за все, знайдемо ефективний коефіцієнт жорсткості
Розв’язок. Перш за все, знайдемо ефективний коефіцієнт жорсткості  . В нашому випадку, коли пружини закріплено паралельно:
. В нашому випадку, коли пружини закріплено паралельно:
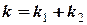 = 200 (Н/м).
= 200 (Н/м).
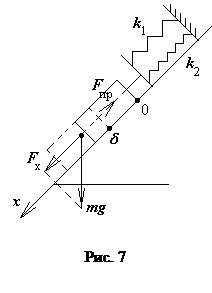
Проведемо вісь 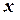 вздовж похилої площини з початком у точці закріплення тіла (рис. 7). Положення рівноваги (
вздовж похилої площини з початком у точці закріплення тіла (рис. 7). Положення рівноваги (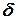 ) визначимо з умови рівності сили пружності
) визначимо з умови рівності сили пружності 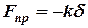 і проекції сили тяжіння на похилу площину
і проекції сили тяжіння на похилу площину 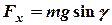
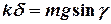 ,
,
звідки отримаємо
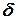 = 0,018 (м).
= 0,018 (м).
Запишемо диференціальне рівняння вільних незатухаючих коливань відносно нового положення рівноваги
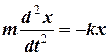 , або
, або 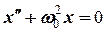 .
.
Кругову частоту коливань легко підрахувати
 = 20 (рад/с).
= 20 (рад/с).
Розв’язок диференціального рівняння коливань запишемо в вигляді
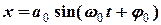 .
.
Амплітуду та початкову фазу визначимо за формулами (7) та (8):
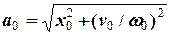 =
= 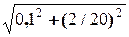 = 0,14 (м),
= 0,14 (м),
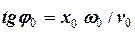 = 0,1·20/(- 2,0) = -1.
= 0,1·20/(- 2,0) = -1.
З останнього рівняння отримаємо
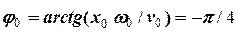 = - 0,785 (рад).
= - 0,785 (рад).
Перевіримо, чи задовольняють нас отримані результати. Для цього підставимо значення 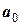 і
і 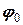 в (4), (5) та підрахуємо зміщення
в (4), (5) та підрахуємо зміщення 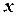 та швидкість
та швидкість 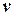 на момент часу
на момент часу 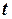 = 0:
= 0:
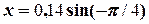 = - 0,1 (м) =
= - 0,1 (м) = 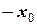 ,
,
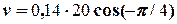 = 2 (м/с) =
= 2 (м/с) = 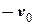 .
.
Як ми бачимо, отримані значення початкового зміщення та швидкості мають протилежний знак щодо умов завдання. Це наслідок того, що арктангенс береться у межах від - 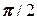 до
до 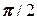 . Оскільки період функції тангенс дорівнює
. Оскільки період функції тангенс дорівнює
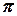 = 3,14, додамо
= 3,14, додамо 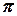 до знайденого значення арктангенса і отримаємо нове значення початкової фази
до знайденого значення арктангенса і отримаємо нове значення початкової фази
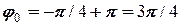 = 2,356.
= 2,356.
Остаточна перевірка дає:
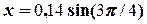 = 0,1 (м) =
= 0,1 (м) = 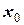 ,
,
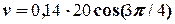 = -2,0 (м/с) =
= -2,0 (м/с) = 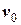 .
.
Отож, рівняння вільних коливань має вигляд
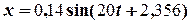
Відповідь: 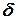 = 0,018 м,
= 0,018 м,  = 20 рад/с,
= 20 рад/с, 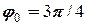 рад,
рад, 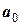 = 0,14 м,
= 0,14 м,
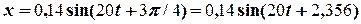 м.
м.
Date: 2015-08-15; view: 570; Нарушение авторских прав