Основные сведения из термодинамики

Первое начало термодинамики представляет собой частную форму применительно к тепловым процессам всеобщего закона природы - закона превращения и сохранения энергии. Для ква­зистатических процессов он формулируется следующим образом: подведенное к единице массы газа бесконечно малое количест­во тепла 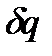расходуется на повышение внутренней энергии газа 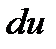и на выполнение термодинамической работы

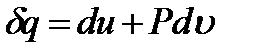(1.8)

где 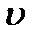- удельный объем, определяемый по формуле (1.2).

Формальное интегрирование выражения (1.8) позволяет найти полное количество тепла, которое подведено к газу в процессе изменения его состояния от начального 1 до конечного 2.

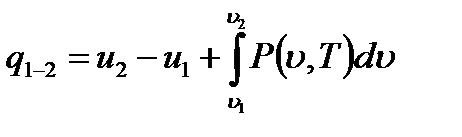(1.9)

Интеграл, стоящий в правой части равенства (1.9), представляет работу термодинамического процесса расширения и зависит от характера процесса, т.е. вида кривой, соеди­няющей точки 1 и 2 на поверхности 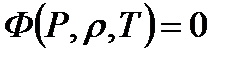. Это указывает на то, что 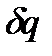, входящее в равенство (1.8), не является полным дифференциалом. Однако, если обе части равенства (1.8) умножить на интегрирующий множитель 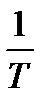, то выражение 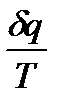становится полным диффе­ренциалом некоторой функции состояния 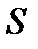, называемой эн­тропией, т.е.

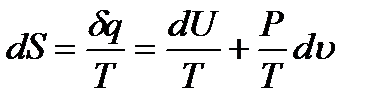(1.10)

При переходе газа из состояния 1 в состояние 2 изме­нение 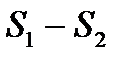не зависит от характера процесса пере­хода, а целиком и полностью определяется начальным и ко­нечным состояниями.

Следует обратить внимание, что равенство (1.10) справедливо для обратимых процессов. Обратимым называется процесс изменения состояния, который, будучи переведен в обратном направлении, возвращает систему в первоначальное состояние через те же промежуточные состояния без каких- либо изменений в окружающей среде.

Необратимые процессы изменения состояния определяются условием

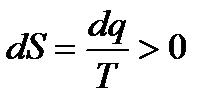(1.11)

Неравенство (1.11) является математическим выражени­ем второго начала термодинамики, которое характеризует на­правление протекающих в природе макроскопических процессов. Второе начало термодинамики позволяет установить количест­венное соотношение между работой, которая могла бы быть совершена системой при обратимом процессе, и действительной работой.

При изучении закономерностей движения газа необходимо учитывать термодинамический процесс изменения состояния га­за. При этом различают изотермический, адиабатный, изоэнтропийный, изоэнтальпийный процессы.

Процесс, происходящий без теплообмена системы с окружающей средой, называется адиабатным. Процесс в системе, при котором сохраняется неизменной энтропия системы, назы­вается изоэнтропийным. Изоэнтропийный процесс - это не что иное как обратимый адиабатный процесс. Он возможен в энерге­тически изолированной системе при отсутствии трения между частицами газа. При наличии трения между частицами газа адиабатный процесс будет неизоэнтропийным. Выделяющееся внутри системы тепло, обусловленное работой сил трения при­водит к возрастанию энтропии 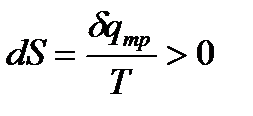и, конеч­но, процесс при этом будет необратимым.

Процесс в системе, характеризуемый постоянством эн­тальпии, называется изоэнтальпийным.

Энтальпией (теплосодержанием), отнесенной к единице массы, называется функция

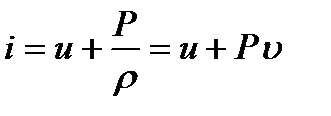(1.12)

которая определяется только состоянием газа, например, тем­пературой и давлением.

Рассмотрим основные соотношения термодинамических пара­метров для идеального газа, которые будут использоваться в дальнейшем при изложении курса.

Подведенное к системе тепло 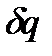приведет к новому состоянию газа с параметрами 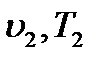. Количество подведенного тепла 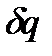можно выразить через удельную тепло­емкость газа при постоянном давлении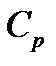

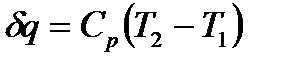(1.13)

С другой стороны, согласно первому началу термодина­мики подведенное тепло идет на изменение внутренней энер­гии газа, которое в соответствии с (1.5) равно 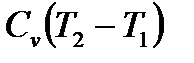, и на выполнение работы расширения газа 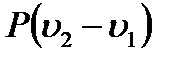. Сле­довательно,

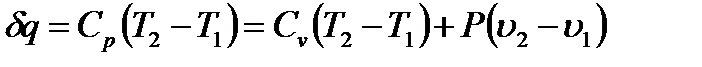(1.14)

Второе слагаемое в правой части равенства (1.14) можно преобразовать, используя уравнение состояния (1.3), к виду

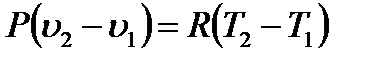(1.15)

Если теперь заменить второе слагаемое в (1.14) по формуле (1.15), то после сокращения на величину 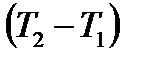получим известное в термодинамике выражение Майера

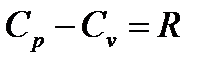(1.16)

Используя соотношения (1.3), (1.5) и (1.16), можно получить иные выражения для энтальпии 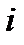. В самом деле, из (1.12) имеем

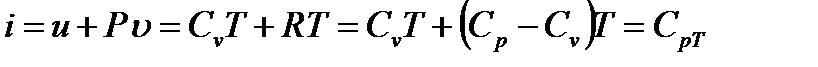(1.17)

Последнее выражение предстанет в ином виде, если в нем заменить 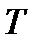по формуле (1.3)

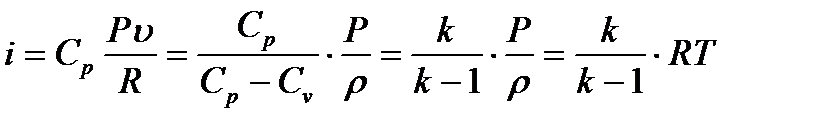(1.18)

где 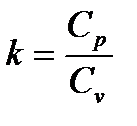(1.19)

Изменение энтропии 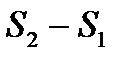при переходе идеального газа из состояния 1 в состояние 2 определится интегрирова­нием (1.10), которое с учетом выражений (1.5) и (1.3) дает

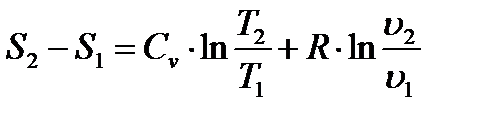
или, если использовать формулу Майера (1.16)

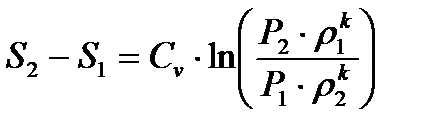(1.20)

Используя (1.20), получается уравнение адиабаты Пуассона, описывающее изоэнтропийный (обратимый адиабат­ный) процесс изменения состояния газа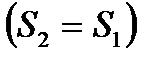

(1.21)

Показатель степени 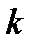, входящий в (1.21) и оп­ределяемый формулой (1.19), называется показателем адиа­баты Пуассона.

2. ОСНОВНЫЕ ЗАКОНЫ СЖИМАЕМОЙ СРЕДЫ

Date: 2015-08-15; view: 539; Нарушение авторских прав