Спектральное описание пространственной структуры поля

Поле световой волны, распространяющейся в свободном пространстве, подчиняется волновому уравнению: 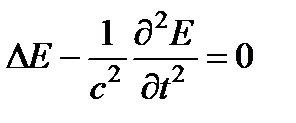, где ,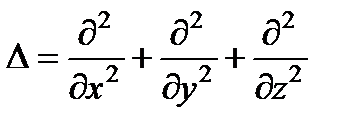

D – оператор Лапласа. Ограничимся рассмотрением дифракции монохроматической волны. Полагая

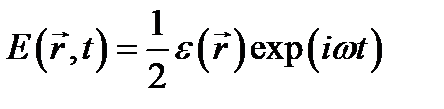+ к. с.,

получим для комплексной амплитуды 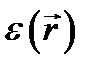уравнение Гельмгольца: ,

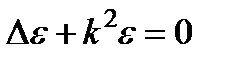где k = w /c. Задача дифракции состоит в отыскании решения уравнения, удовлетворяющего граничному условию .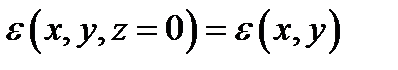

Такое условие возникает, например, при прохождении света через экран типа "чёрная маска", плоский транспарант, вносящий фазовую неоднородность и т.п.

Разложим двумерное световое поле e ₀(x, y), заданное в начальном сечении z = 0, в интеграл Фурье

.

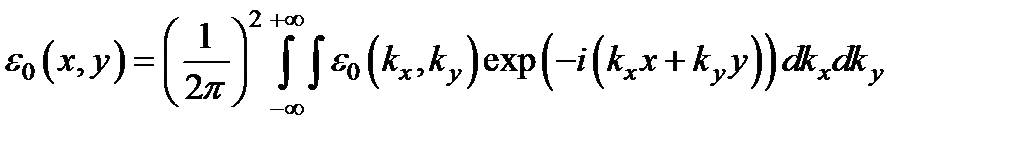Здесь пространственная спектральная амплитуда e ₀(k_x, k_y) определяется обратным преобразованием Фурье: .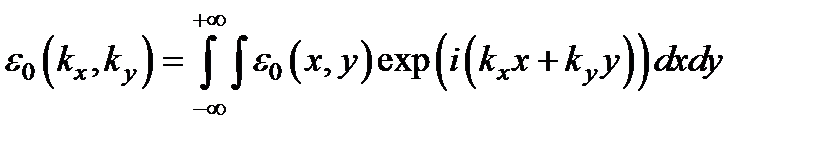

Световое поле e (x, y, z) в произвольной точке пространства ищем в виде, аналогичном, но со спектральной амплитудой, зависящей от z: .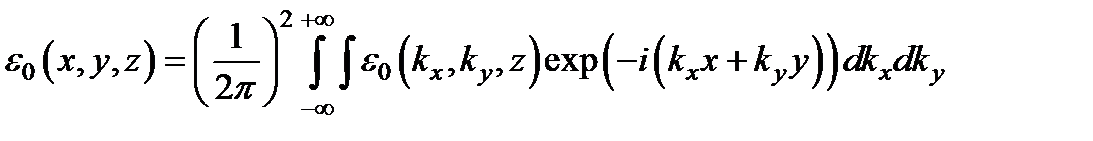

Подставляя в, находим уравнение для спектральной амплитуды e (k_x, k_y, z):

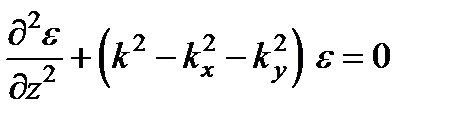и его решение

.

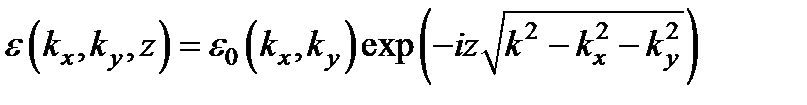Подставив теперь в, получим

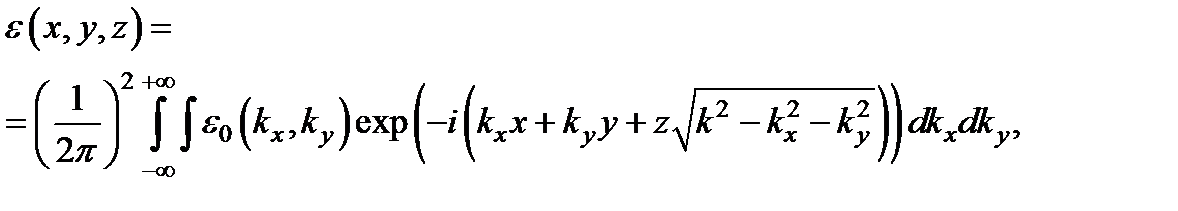
или, с учетом ,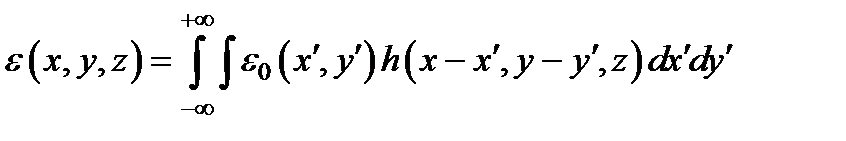

где введена функция ,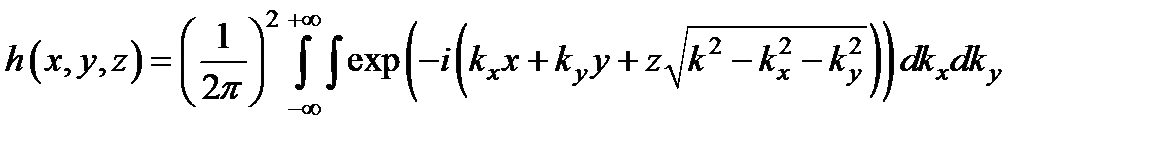

называемая функцией Грина данной линейной системы. Введем так же функцию

,

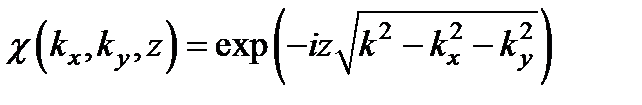называемую частотным коэффициентом передачи системы. Из формул и следует, что

.

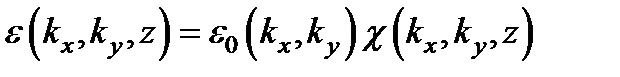Кроме того, в силу,

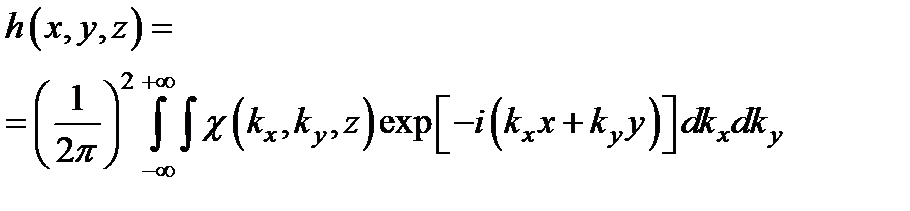
и, следовательно, .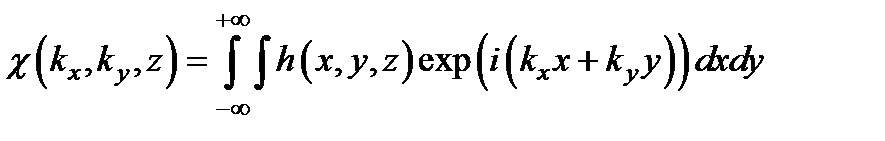

Таким образом, частотный коэффициент передачи и функция Грина связаны между собой преобразованием Фурье. Это общее свойство всех линейных систем.

Прямой подстановкой, в, нетрудно проверить, что найдено точное решение задачи дифракции. Простота решения указывает на адекватность использованного математического метода физическому содержанию задачи дифракции.

Инварианты распространения светового пучка.

Введём интенсивность J, мощность P и угловой спектр S (k_x, k_y) светового пучка, определив их формулами:

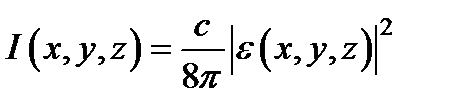, (в Гауссовой системе) ,

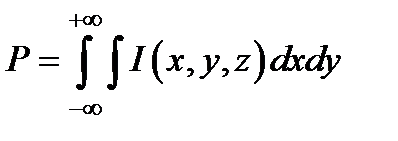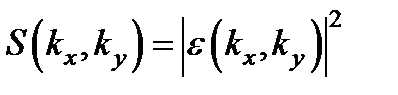. В силу теоремы Парсеваля:

.

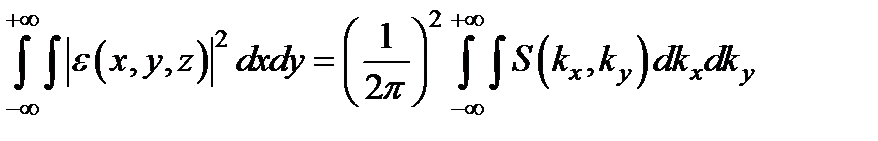Из формул,, – следует, что угловой спектр пучка и его полная мощность не зависят от z, т.е. являются инвариантами распространения:

,

.

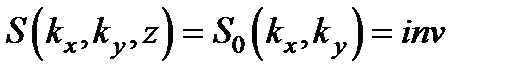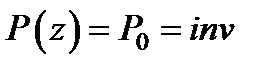Нетрудно проверить, что результаты конкретных расчетов, проделанных выше, удовлетворяют общим соотношениям,. Формула раскрывает причину устойчивости картины фраунгоферовой дифракции. Согласно этой формуле, картина дифракции, возникающая в дальней зоне, устойчива потому, что она повторяет форму углового спектра пучка, а угловой спектр является инвариантом распространения.

Date: 2015-08-06; view: 511; Нарушение авторских прав