Дифракция Фраунгофера на отверстиях произвольной формы

Рассмотрим теперь дифракцию Фраунгофера при падении плоской волны на отверстие в экране. В отличие от длинной щели здесь волны дифрагируют во всех направлениях. Каждой точке наблюдения Р соответствует определенное направление дифрагировавших волн, характеризуемое единичным вектором 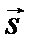(рис. 4.28).

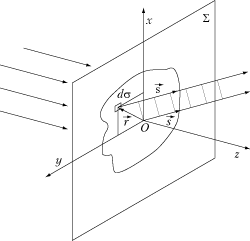
Р и с. 4.28

В качестве вспомогательной поверхности ξ выберем плоскость экрана xОy. Разность хода идущих по направлению 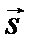вторичных волн из элемента ds этой поверхности и из начала координат O равна проекции вектора , определяющего положение ds в плоскости xОy на направление 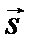, т.е. ( 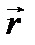× 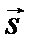). В соответствии с принципом Гюйгенса-Френеля напряженность поля в точке Р пропорциональна интегралу по всей площади отверстия в экране: ,

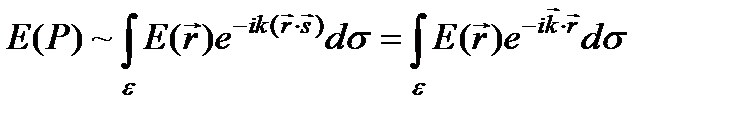где 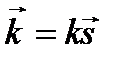– волновой вектор света, дифрагировавшего в направлении 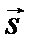. Опущенный в коэффициент наклона K (q) можно считать постоянным, когда размеры отверстия много больше длины волны, и заметную интенсивность имеют лишь волны, дифрагировавшие на малые углы. Напряженность 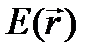в плоскости xОy, считается равной напряженности поля падающей волны в пределах отверстия экрана и равной нулю за его пределами. Понимая функцию E (x, y) именно так, можно распространить интегрирование в на всю плоскость xОy: .

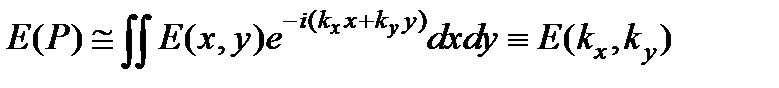Отсюда видно, что поле в фраунгоферовой дифракционной картине, т.е. в фокальной плоскости объектива, представляет собой (с точностью до постоянного множителя) двухмерное преобразование Фурье функции E (x, y), описывающей поле в плоскости xОy. Функция E (k_x, k_y), т.е. фурье-образ искаженного препятствием волнового поля E (x, y) в плоскости xОy, пропорциональна комплексной амплитуде плоской волны, дифрагировавшей в определенном направлении k_x, k_y. Пространственное разделение волн, дифрагировавших в разных направлениях, позволяет наблюдать отдельные фурье-компоненты функции E (x, y). Поэтому можно считать, что в дифракции Фраунгофера физически осуществляется разложение функции E (x, y) в двухмерный интеграл Фурье.

При нормальном падении плоской волны на прямоугольное отверстие со сторонами a и b, параллельными осям x и y из находим: 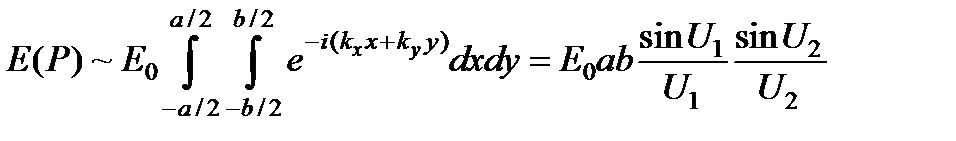, где U ₁ = k_xa /2, U ₂ = k_yb /2, E ₀ – амплитуда волны в плоскости экрана с отверстием. Распределение интенсивности в дифракционной картине определяется формулой .

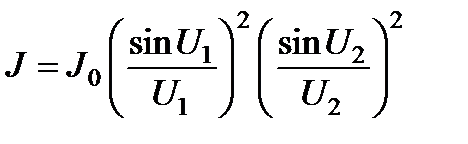Когда длина одной из сторон много больше длины другой, мы приходим к выражению для дифракции на длинной щели. В дифракционной картине от прямоугольного отверстия (рис. 4.29) распределение интенсивности в соответ-ствии с дается произведением распределений от взаимно перпендику-лярных щелей.

Р и с. 4.29

Интенсивность равна нулю вдоль двух рядов линий, параллельных сторонам прямоугольника. Заметную интенсивность имеют лишь средние цепочки максимумов, образующие "крест" на рис. 4.29а. Относительная высота максимумов интенсивности, расположенных вдоль этих линий, характеризуется соотношением

1: 0,047: 0,017: …» 1: [2/3 p ]²: [2/5 p ]²: …

Величина остальных максимумов столь мала (0,2% для ближайших к центру), что они трудно наблюдаемы. Большая часть светового потока приходится на центральный максимум, и именно его можно рассматривать как изображение находящегося в фокусе коллиматора точечного источника, получающееся в

Р и с. 4.30

фокальной плоскости объектива при ограничении сечения, формирующего изображение пучка света прямоугольной диафрагмой. Это изображение шире в направлении более короткой стороны прямоугольника.

Дифракция Фраунгофера от круглого отверстия представляет большой практический интерес, так как в оптических приборах оправы линз и объективов, а также диафрагмы имеют обычно круглую форму. При вычислении интеграла целесообразно перейти к полярным координатам r и j в плоскости отверстия: x = r cos j, y = r sin j. Направление дифрагировавшей волны, соответствующее точке Р, удобно характеризовать углом q с осью Оz и азимутальным углом y: k_x = k sin q cos y, k_y = k sin y sin q. Тогда k_xx + k_yy = kr sin q cos(j – y) и интеграл принимает вид ,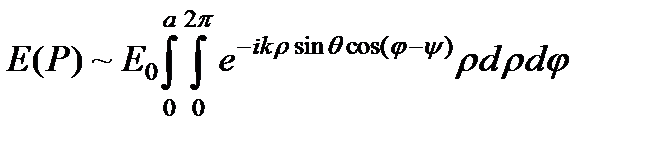

rdrdj – элемент площадки, a – радиус отверстия. Используя интегральное представление для бесселевых функций нулевого порядка ,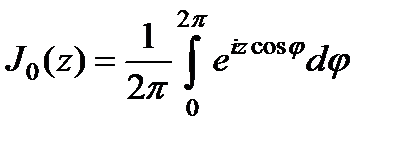

выразим E (p) через интеграл от J ₀(kr sin q), который вычисляется с помощью соотношения

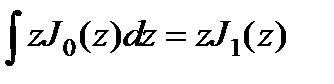, где J ₁(z) – функция Бесселя первого порядка.

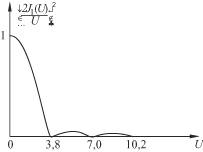
Дифракционная картина от круглого отверстия имеет вид концентрических светлых и темных колец (рис.4.29б) со следующим радиальным распределением интенсивности:

,

где q – угол дифракции. График этой функции приведен на рис. 4.30. Она имеет главный максимум при U = 0 и с ростом U осциллирует с быстрым уменьшением амплитуды, подобно функции (sin U / U)², описывающей дифракцию на щели. Угловые радиусы q_m темных колец равны 0,61 l / a, 1,12 l / a, 1,62 l / a. Расстояние между соседними кольцами с увеличением их номера приближается к l /2 a. Эффективный размер дифракционной картины и здесь обратно пропорционален размеру отверстия. Интенсивность максимумов быстро уменьшается: уже в ближайшем максимуме она составляет менее 2% от интенсивности центрального максимума, на который приходится 84% проходящего через отверстие светового потока. Поэтому центральный максимум (диск Эйри), имеющий угловой радиус ,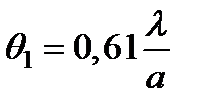

можно рассматривать как изображение точечного источника, уширенное дифракцией на круговой диафрагме радиусом a. Соотношение играет важную роль в вопросе о разрешающей силе оптических инструментов.

Важно отметить, что распределение интенсивности в фраунгоферовой дифракционной картине не изменится, если отверстие сместить в плоскости экрана в сторону, не изменяя его ориентации. Картина в фокальной плоскости объектива всегда симметрична по отношений к его оси независимо от положения отверстия. Особый интерес представляет случай, когда в экране имеется большое число N одинаковых отверстий. При правильном, регулярном, расположении отверстий, когда их ориентация и расстояния между ними одинаковы, разность фаз между волнами, дифрагировавшими от соседних отверстий, имеет определенное значение. Интерференция этих волн существенно влияет на дифракционную картину. В направлениях, для которых разность фаз кратна 2 p, амплитуда дифрагировавших волн в N раз больше, а интенсивность в N ² раз больше, чем от одного отверстия. Такое резкое увеличение интенсивности для некоторых направлений имеет большое практическое значение. Случай регулярного расположения отверстий подробно рассмотрен на примере дифракционной решетки.

При хаотическом, беспорядочном расположении отверстий фазовые соотношения между волнами от отдельных отверстий имеют случайный характер. Поэтому для каждого направления наблюдения происходит простое сложение интенсивностей волн, дифрагировавших от всех отверстий. Распределение интенсивности в дифракционной картине от одного отверстия не зависит от его положения. От большого числа N отверстий получается такая же картина, усиленная по интенсивности в N раз.

Date: 2015-08-06; view: 631; Нарушение авторских прав