Интегральная теорема Кирхгофа-Гельмгольца

Согласно этой теореме, амплитуду поля в некоторой точке P можно вычислить, если известна амплитуда поля e и ее производная по нормали ¶ e /¶ n на какой-либо поверхности S, охватывающей точку Р. А именно:

, ,

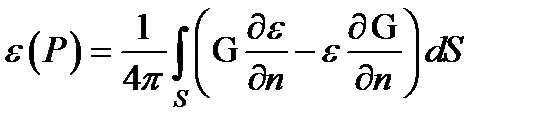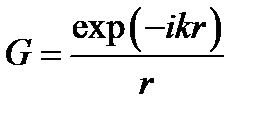G – функция точечного источника, или функция Грина для уравнения Гельмгольца.

Р и с. 4.31

Применительно к задаче дифракции Кирхгоф предложил использовать следующие приближенные граничные условия для светового поля: в пределах отверстий поле таково, как если бы препятствий нет, а на теневой стороне экранов поле равно нулю. Ввиду малости длины световой волны эти приближенные условия обеспечивают достаточную точность вычислений.

Для задачи о дифракции сферической световой волны на отверстии теория Кирхгофа дает следующий результат: ,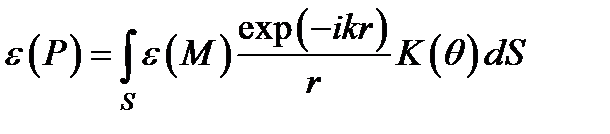

Где .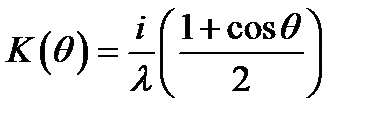

Интеграл в точности совпадает с дифракционным интегралом Гюйгенса-Френеля. Однако вид функции K (q), предполагаемый Френелем, оказывается не совсем точным. График функции показан на рис. 4.32.

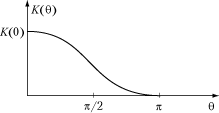
Р и с. 4.32

Основной вклад в дифракционный интеграл вносят центральные (приосевые) зоны Френеля, для которых q << 1. Полагая K (q) = K (0) = i / l получим .

В такой форме дифракционный интеграл совпадает с интегралом Гюйгенса-Френеля. Коротко остановимся на выводе формул,.

Пусть есть точечный монохроматический источник света, расположенный в точке P ₀. Вычислим световое поле в некоторой точке P при условии, что между точками Р ₀ и Р имеется препятствие, например, экран с отверстием (рис. 4.33).

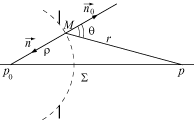
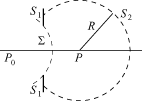
Р и с. 4.33 Р и с. 4.34

Согласно теории Кирхгофа-Гельмгольца, дифракционное световое поле в точке P определяется интегралом по произвольной поверхности S, охватывающей эту точку. Выберем поверхность S состоящей из трех частей: поверхности x, стягивающей отверстие в экране, поверхности S ₁ теневой части экрана и сферической поверхности S ₂ достаточно большого радиуса R с центром в точке Р. Вид поверхности S показан на рис. 4.34.

Физические соображения показывают, что основной вклад в световое поле в точке P должен давать интеграл по поверхности x, поскольку именно через отверстие в экране свет от источника проникает в точку P. Следовательно, ,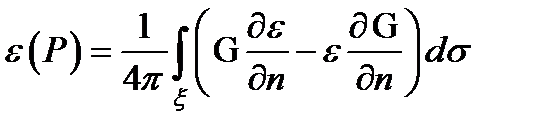

где G – функция Грина, r – расстояние между точками M и P, 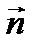– единичный вектор внутренней нормали к поверхности x в точке M. Поверхность x удобно выбрать в виде сферической поверхности с центром в точке P ₀, где расположен точечный источник света.

Вычислим производную ¶G/¶ n. Как видно из рис. 2 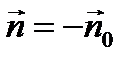. Поэтому можно записать ¶G/¶ n = – ¶G/¶ n ₀. Воспользуемся правилом дифференцирования сложной функции: ;

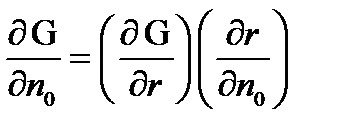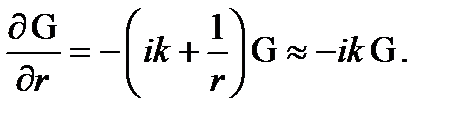Поскольку в оптике, как правило, r >> l и, следовательно, k >> 1/ r, то это приближение, называемое оптическим, обычно обеспечивает достаточную точность.

Как видно из рис. 4.35, .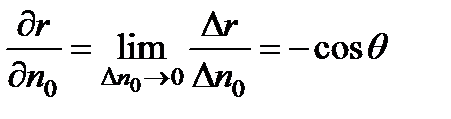

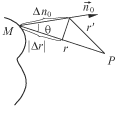
Р и с. 4.35

Таким образом, .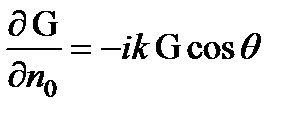

Теперь вычислим производную ¶ e /¶ n. Так как эта производная вычисляется в точке M на поверхности x,

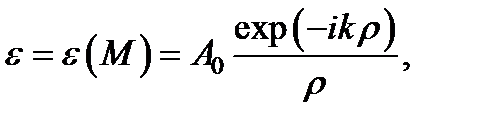
где A ₀ – постоянная, r – расстояние от точки Р ₀ до точки М. Выполняя вычисления подобно тому, как это было сделано для производной ¶G/¶ n, получим ,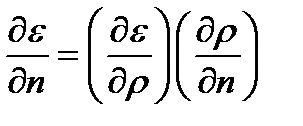

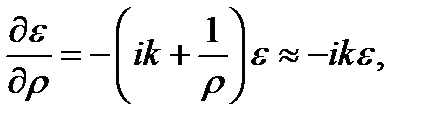
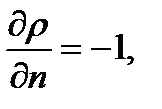, так что: .

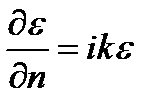Подставляя,, в, получим,.

Показано, что приближенное решение волнового уравнения для светового поля, данное Кирхгофом, подтверждает френелевскую теорию дифракции, В настоящее время теория Френеля сохраняет свое значение, прежде всего, как система наглядных образов, хорошо раскрывающая физику дифракции света. Формулировка задачи дифракции, основанная на теории Максвелла, позволяет использовать для решения дифракционных задач хорошо разработанный аппарат математической физики, в частности, метод спектрального разложения, метод параболического уравнения, а также применять мощные и универсальные методы численного моделирования.

Основные понятия Фурье-оптики

Идеи и методы, связанные с направленным воздействием на световые поля с целью формирования заданной структуры поля, объединяют понятием ”фурье-оптика". Тем самым подчёркивается основополагающая роль спектральных представлений для решения задач, связанных с анализом, преобразованием и синтезом световых полей.

Спектральное разложение, основанное на преобразовании Фурье, позволяет представить произвольное световое поле со сложной пространственно-временной структурой в виде суперпозиции плоских монохроматических волн. В силу линейности волнового уравнения, каждая из этих волн распространяется в вакууме или в линейной оптической среде независимо от других волн, что дает возможность свести анализ преобразования сложного поля к задаче о преобразовании элементарной волны. Результирующее поле находят затем путем суммирования прошедших через систему плоских монохроматических волн.

Указанные процедуры – анализ, преобразование и синтез световых полей – являются не только просто математическими операциями, но во многих случаях отчётливо проявляются как реальные физические процессы. Так, при свободной дифракции светового пучка в дальней зоне формируется устойчивое пространственное распределение интенсивности излучения, повторяющее по форме угловой спектр пучка. Такую же форму, только в значительно меньшем масштабе, имеет распределение поля в фокальной плоскости линзы. В обоих случаях осуществляется пространственное спектральное разложение поля. Различные операции над световыми полями, выполняемые в фокальной плоскости линзы с помощью разного рода экранов, масок, фазовых пластин, являются пространственными аналогами частотной фильтрации электрических колебаний, применяемой в радиотехнике.

Date: 2015-08-06; view: 906; Нарушение авторских прав