Коэффициент передачи тонкой линзы

Рассмотрим линзу, для которой луч, входящий в точке с координатами x, y на одной поверхности выходит на другой поверхности в точке с такими же координатами. Разумеется, данное условие является приближенным, однако оно выполняется тем точнее, чем тоньше линза. Этим и объясняется термин "тонкая" линза.

Определим комплексный коэффициент передачи тонкой линзы t (x, y) как отношение комплексных амплитуд прошедшей и падающей волн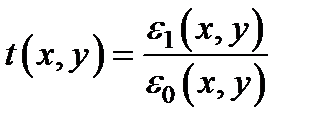

Для вычисления этой характеристики линзы необходимо описать распространение света в стекле. Распространение света в различных оптических средах будет подробно рассмотрено ниже. Здесь же воспользуемся одним простым результатом, необходимым нам для расчёта. Этот результат заключается в том, что в прозрачной линейной изотропной оптической среде световая волна распространяемся со скоростью ,,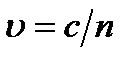

где c – скорость света в вакууме, n – действительная положительная величина, большая единицы, называемая показателем преломления среды.

Принимая во внимание последнее соотношение, запишем световую волну в стекле в виде

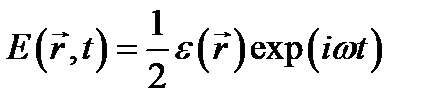+ к. с., где комплексная амплитуда: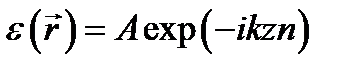

и k = w /c = 2 p / l ₀, l ₀ – длина волны в вакууме.

Р и с. 4.38

Обозначим через D (x, y) толщину линзы в точке с координатами x, y, а через D₀ – её максимальную толщину (рис. 4.38).

Тогда нетрудно показать, что коэффициент передачи линзы есть

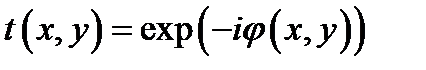, где .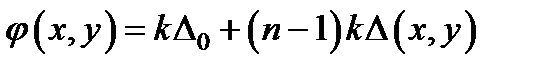

Теперь вычислим функцию D (x, y). Сделаем это на примере плосковыпуклой линзы, показанной на рис. 4.39. Как видно из этого рисунка, ,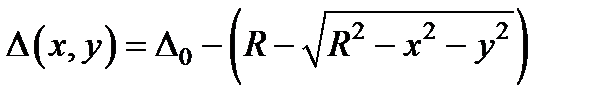

где R – радиус кривизны сферической поверхности линзы. Полагая, что

Р и с. 4.39

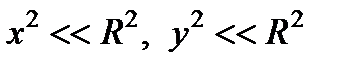
(“параксиальное” приближение), запишем выражение для D (x, y) в виде: .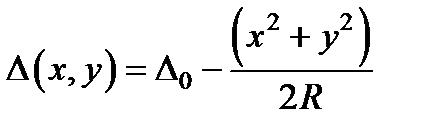

Тогда коэффициент передачи линзы приобретает вид .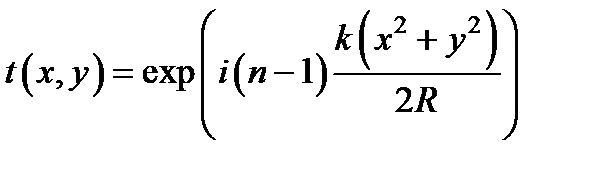

Для упрощения записи мы опустили здесь постоянный фазовый множитель.

Далее введём фокусное расстояние линзы f, определив его формулой:

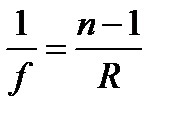. Тогда .

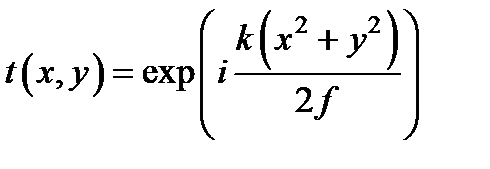В такой форме коэффициент передачи описывает не только плосковыпуклую, но и вообще любую тонкую линзу.

Date: 2015-08-06; view: 632; Нарушение авторских прав