Дифракционная решётка

Исследование дифракции на двух щелях показывает, что в этом случае дифракционные максимумы становятся более узкими, чем в случае одной щели. Увеличение числа щелей делает это явление ещё более отчётливым.

Рассмотрим сейчас правильную структуру, состоящую из множества (до сотен тысяч) одинаковых равноотстоящих параллельных щелей, сделанных в непрозрачном экране. Такая структура называется дифракционной решёткой. Пусть дифракционная решётка имеет N щелей, ширина каждой из них b, промежуток между щелями a, период решётки d = a + b. В решётке осуществляется многолучевая интерференция дифрагированных пучков света, исходящих от щелей решётки при ее когерентном освещении. Дифракционная картина наблюдается по методу Фраунгофера, т.е. либо на бесконечно удалённом экране, либо в фокальной плоскости линзы, поставленной на пути дифрагированного света.

Найдем в этой случае распределение интенсивности по углам дифракции j. Предположим, что на решетку перпендикулярно к ее поверхности падает плоская монохроматическая волна (рис. 4.26).

Разность хода между дифрагированными волнами, исходящими из соседних щелей решетки, будет D = d sin j, а разность фаз – d = k D = kd sin j, где j – угол дифракции. Обозначим, как и раньше, через E ₁, возмущение, создаваемое в точке наблюдения первой щелью. Оно определяется формулой 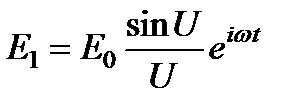. 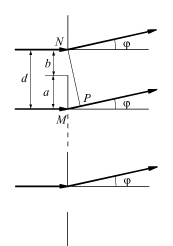Р и с. 4.26

Возмущения, создаваемые остальными щелями, представятся выражениями:

.

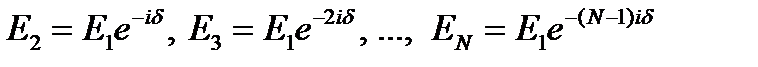Полное поле, создаваемое по этому направлению всеми щелями, представится суммой

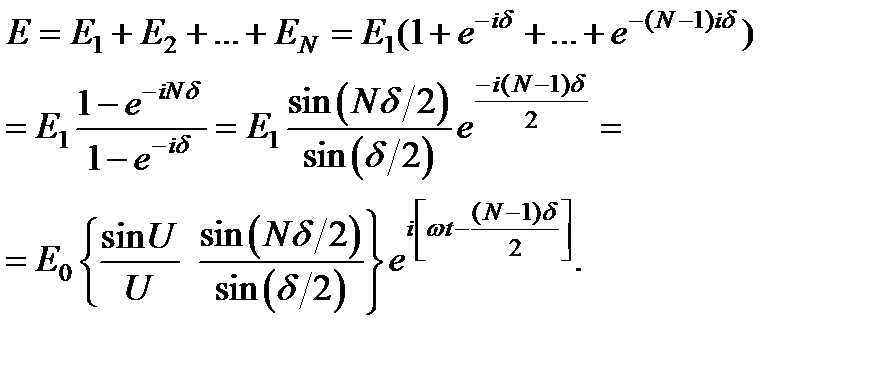
Выделим комплексную амплитуду А суммарного возмущения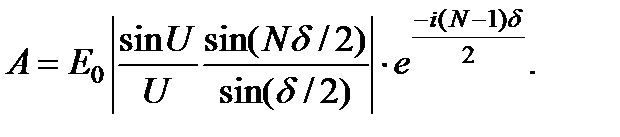

Определим искомую интенсивность дифрагированного света как 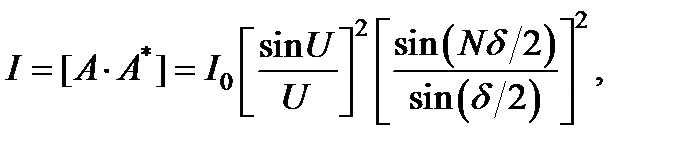где 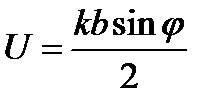, 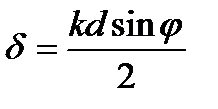.Первых два сомножителя в описывают дифракцию на одной щели (рис. 4.27а). Проанализировав его, получим условие главных дифракционных минимумов: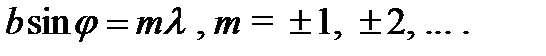

Третий сомножитель в определяет интерференцию параллельных пучков без учета дифракции (рис. 4.27б). Из него следуют условия главных максимумов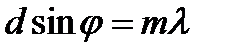

и дополнительных интерференционных минимумов: ,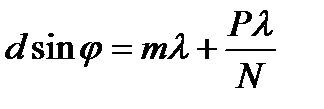

m = 0, ±1, ±2, …; P = 1, 2, …, N – при каждом значении m) График распределения пронормированной к единице относительной интенсивности, определяемой соотношением, представлен на рис. 4.27в. Формулы – – основные в теории дифракционной решетки.

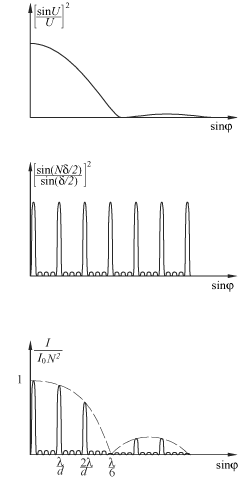Р и с. 4.27

Условие определяет направления, в которых излучения от всех щелей решетки приходят в точку наблюдения в одинаковых фазах, а поэтому усиливают друг друга. По этим направлениям получаются максимумы, интенсивность которых в N ² раз превосходит интенсивность волны от одной щели в том же направлении. Целое число m называют порядком главного максимума или порядком спектра. Из условия видно, что угол j, под которым наблюдается определенный максимум, зависит не только от параметра решетки, но и от длины волны света. Это позволяет использовать дифракционную решетку для разложения излучения на монохроматические составляющие, т.е. в спектр.

Когда d sin j = ml, d /2 = mp и множитель 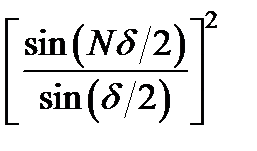принимает неопределённый вид. Раскрыв неопределенность, получим на основе интенсивность m -го максимума:

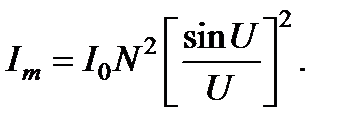Подставив sin j = (ml)/ d в U = (pb sin j)/ l, перепишем следующим образом: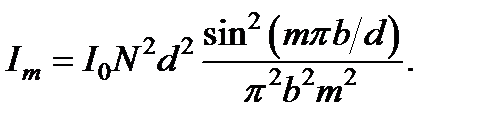

Анализ этой формулы приводит к следующим выводам:

1. Интенсивность в главных максимумах в N ² раз превосходит интенсивность, создаваемую по этим направлениям одной щелью.

2. I_m ~ 1/ m ², т.е. с увеличением порядка максимума резко уменьшается его интенсивность.

3. Интенсивность в m -ом максимуме существенно зависит от отношения b / d. При (b / d) m= 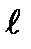, где 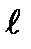– целое число, выражение обращается в нуль. т.к. sin( 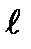p)=0, т.е. интенсивность в этом максимуме равна нулю. В данном случае совпадают условия возникновения главного максимума интерференционной картины на N щелях и минимума дифракции на каждой щели. Так, например, при b / d = 1/3 выпадает каждый третий максимум в дифракционной картине, что и показано на рис. 4.27в.

Из выражения следует, что между двумя главными максимумами должно возникать (N – 1) интерференционных минимумов, когда sin(Nd /2) = 0, а sin(d /2) ¹ 0, что и определяет условие минимумов. Между этими минимумами должны находится побочные, или дополнительные максимумы, в которых интенсивность света при достаточно большом N пренебрежимо мала по сравнению с интенсивностями главных максимумов.

Согласно формулам и угловое расстояние D j между любым главным максимумом и соседним минимумом определяется из требования, чтобы разность хода возросла на l / N, т.е. D(d sin j) = l / N, откуда d cos j ×D j = l / N, так что D j = l /(Nd cos j). При не очень больших углах дифракции (cos j»1) резкость главных максимумов не зависит от порядка спектра и равна .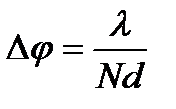

Из формулы следует, что резкость главных максимумов тем больше, чем больше Nd, т.е. чем больше общая ширина решетки. При заданном периоде решетки d резкость главных максимумов возрастает (D j уменьшается) с ростом числа штрихов N.

Date: 2015-08-06; view: 1303; Нарушение авторских прав