Дифракция Фраунгофера на щели

Рассмотрим сначала простой, но практически важный случай, когда отверстие в экране имеет вид узкой длинной щели с параллельными краями (рис. 4.22). Будем считать, что размер волновой поверхности в направлении вдоль щели ограничен только диаметром объектива, и если вносимую им дополнительную дифракцию не принимать во внимание, то волны дифрагируют только в направлениях, перпендикулярных щели.

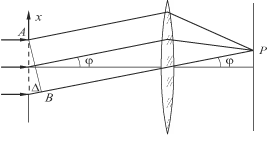
Р и с. 4.22

Распределение интенсивности в дифракционной картине можно найти с помощью принципа Гюйгенса-Френеля. Задача состоит в определении E _p в любой точке Р за экраном. При том под E будем понимать любую из компонент векторов 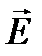или 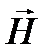электромагнитного поля световой волны. Проведем мысленно поверхность, закрывающую отверстие в экране и ограниченную краями отверстия. Разделим эту поверхность на элементарные участки, малые по сравнению с размерами отверстия, но большие по сравнению с длиной волны. Эти элементарные участки представим в виде узких длинных полосок, параллельных краям щели. Если ширина полосок одинакова, то и площади их будут равными. Можно считать, что каждый из этих участков сам становится источником световой волны, распространяющейся во всех направлениях.

Напряженность, создаваемая элементарным участком в точке наблюдения Р, пропорциональна площади этого участка и напряженности на самом участке, которая создается первичным источником. Надо заметить, что при приближенном решении этой задачи по методу Френеля делается предположение, что напряженность в точках отверстия такова, какой она была бы в случае свободного распространения волны от источника при отсутствии какого бы то ни было экрана, и что в точках, находящихся непосредственно за экраном, напряженность поля равна нулю.

Так как ширина и площадь всех элементарных участков одинакова и все участки имеют одинаковый наклон к направлению наблюдения, то амплитуды вторичных волн равны. При вычислении вклада некоторого участка в результирующее поле E (p) нужно учесть изменение фазы вторичной волны при ее распространении от элемента к точке наблюдения. Соотношение фаз вторичных волн в точке Р будет таким же, как и в любой плоскости, перпендикулярной их направлению до линзы, например, в плоскости AB (рис. 4.22). Из рис. видно, что при нормальном падении света на щель начальные фазы всех вторичных источников одинаковы, так как вспомогательная поверхность, которой мы мысленно закрыли щель, совпадает с фронтом падающей волны.

С учетом всего сказанного рассчитаем полное поле в точке Р как суперпозицию полей вторичных волн от всех элементов поверхности, закрывающей щель в экране. Обозначим ширину всей щели b, а ширину каждого элементарного участка dх, тогда b = Ndx, где N – число элементарных участков. Направление наблюдения зададим углом j. Запишем вторичные волны от всех элементов щели. Пусть для самого крайнего элемента, расположенного вблизи края щели (точки А), имеем: ,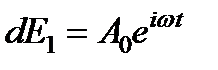

где A ₀ – амплитуда вторичных волн. Вторичная волна от следующего элемента будет иметь такую же амплитуду, но она будет отставать по фазе по отношению к предыдущей волне на некоторую величину d ₀, т.е. 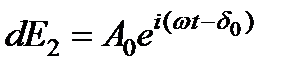. Аналогично для третьего элемента 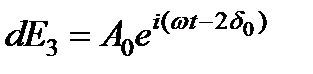. и для N -ного 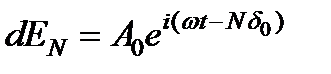. Результат суперпозиции всех вторичных волн представится формулой:

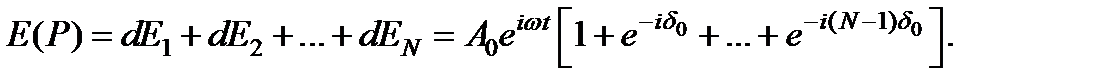
В скобках получилась геометрическая прогрессия, знаменатель которой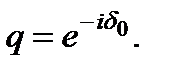

Формулу перепишем в виде:

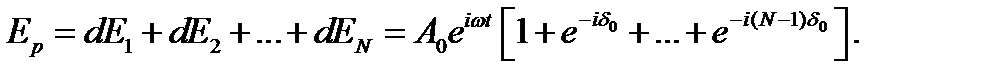
Из формулы следует, что амплитуда результирующего колебания в точке Р, обусловленного вторичными волнами от всей щели шириной b, определяется выражением: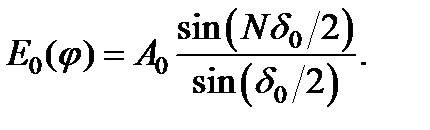

Преобразуем это выражение. Понятно, что Nd ₀ = d, где d – сдвиг фаз вторичных волн от крайних элементов щели. Его можно представить, согласно рис. 4.22, так: .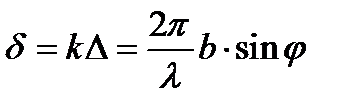

Если число элементов N, на которые мы разбили щель, очень велико, то 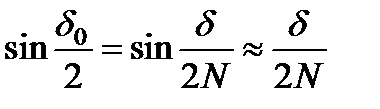, Тогда формула перепишется так: ,

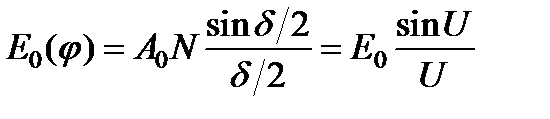где E ₀ = A ₀ N амплитуда суммарного возмущения при j = 0, т.е. по направлению падающей волны а

.

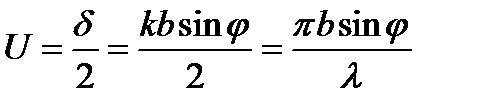Тогда зависимость интенсивности дифрагировавшего света от j определяется выражением:

, где I ₀ – интенсивность света при j = 0.

График распределения интенсивности по направлениям приведен на рис. 4.23. В центре дифракционной картины интенсивность максимальна и равна I ₀. При U = mp, где m = ±1, ±2, … интенсивность равна нулю. Направления j _m на эти минимумы, как видно из, определяются условием .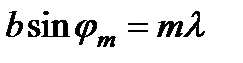

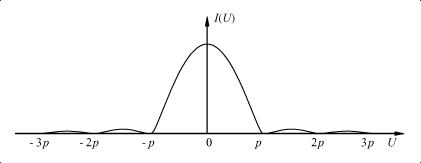Р и с. 4.23

Первый минимум дифракционной картины (m = ±1) соответствует направлению j ₁, для которого sin j ₁ = l / b. Это условие легко получить без всяких вычислений. Рассмотрим две одинаковые элементарные полоски, находящиеся на расстоянии b /2. Вторичные волны от них, распространяющиеся под углом j, имеют разность хода (b /2)sin j. Если эта разность хода равна l /2, т.е. sin j = l / b, то вторичные волны гасят одна другую в результате интерференции. Вся щель состоит из таких пар элементарных полосок, поэтому при sin j=l / b интенсивность дифрагировавшего света обращается в нуль.

Между минимумами интенсивности, определяемыми условием, находятся максимумы различных порядков. Их положение определяется уравнением tg U = U, имеющим корни: U ₀ = 0; U ₁ = 1,43 p; U ₂ = 2,46 p;… Практически можно считать, что максимумы находятся посередине между соседними минимумами, значения интенсивности в максимумах быстро убывают с увеличением порядка. Их отношения приближенно можно выразить в виде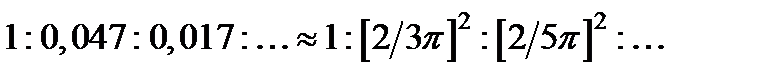

Таким образом, основная часть светового потока сосредоточена в центральной дифракционной полосе между минимумами порядков m = ±1, т.е. в пределах углов – j ₁< j < j ₁, где sin j ₁= l / b. Угловая ширина максимумов уменьшается при увеличении ширины щели: если j << 1, то j ₁= l / b. Центральный максимум становится резче, первые минимумы придвигаются ближе к центру картины. При сужении щели картина расширяется, а ее яркость уменьшается. Когда b приближается к l, центральный максимум охватывает все поле зрения; освещенность экрана уменьшается от центра к краям монотонно.

Если первичный источник точечный, то каждый дифрагированный под определенным углом пучок параллельных лучей соберется линзой в маленькое пятнышко. Такие пятнышки – максимумы и минимумы интенсивностей – расположатся вдоль прямой, перпендикулярной к оси щели и лежащей в фокальной плоскости линзы.

Если в качестве источника света взять светящуюся линию или узкую освещаемую щель, то каждая точка источника даст на экране описанную выше дифракционную картину. В результате наложения таких картин каждое дифракционное пятнышко вытянется в полоску – образуется система дифракционных полос.

Date: 2015-08-06; view: 673; Нарушение авторских прав