Свойства плоской гармонической электромагнитной волны

Для анализа структуры плоской электромагнитной волны удобно записать уравнения Максвелла в символической форме с помощью векторного дифференциального оператора “набла”.

,

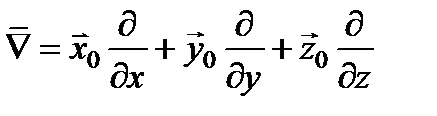где 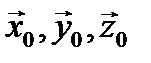– единичные векторы, направленные вдоль осей x, y, z декартовой системы координат.

Принимая во внимание, что для произвольного векторного поля

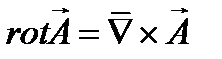
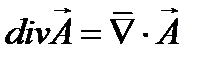уравнения Максвелла (1.1) – (1.4) можно записать так:

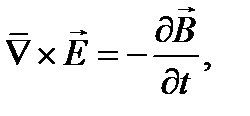
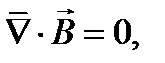
Будем искать решение этих уравнений в виде плоских гармонических волн

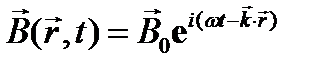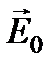, где и 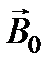– постоянные векторы, не зависящие от времени, но компоненты которых могут быть комплексными. Подставляя выражения и в уравнение – и учитывая, что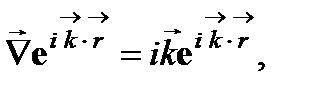

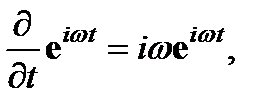
получаем следующие соотношения: , , .

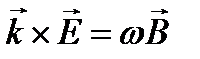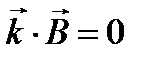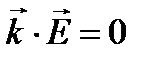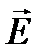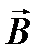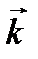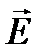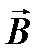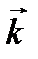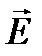Из соотношений и следует, что векторы и плоской волны перпендикулярны вектору , т.е. направлению распространения. Это означает, что электромагнитная волна является поперечной. Соотношения – показывают, что векторы и взаимно перпендикулярны. Таким образом, для плоской гармонической световой волны, распространяющейся в вакууме в произвольном направлении , векторы , и 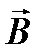образуют правую тройку взаимно перпендикулярных векторов (рис. 1.2).

Р и с. 1.2

Взяв от обеих частей – модули и учитывая взаимную ориентацию всех векторов, а также, что 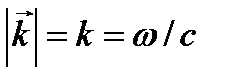, , 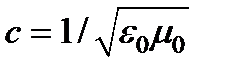, 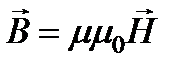находим следующие соотношения между значениями напряженности электрического и магнитного полей, а также между напряженностью электрического поля и магнитной индукцией плоской волны в вакууме: , .

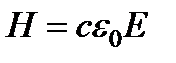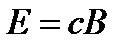На рис. 1.2 видно также, что в бегущей плоской волне 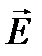и 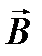изменяются в одинаковой фазе, т.е. одновременно достигают максимальных и нулевых значений.

Date: 2015-08-06; view: 519; Нарушение авторских прав