Волновое уравнение

ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Электромагнитная природа света. Свойства электромагнитных волн

Существование электромагнитных волн было предсказано теоретически Максвеллом как прямое следствие из уравнений электромагнитного поля. Скорость электромагнитных волн в вакууме оказалась равной величине 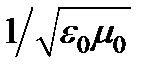. Ее числовое значение почти совпало со скоростью света в вакууме, равной, по измерениям Физо в 1849 г., 3,15× 10⁸ м/с. Другое важное совпадение в свойствах электромагнитных волн и света обусловлено поперечностью волн. Поперечность электромагнитных волн следует из уравнений Максвелла, а поперечность световых волн – из экспериментов по поляризации света (Юнг 1817г.). Эти два факта привели Максвелла к заключению, что свет представляет собой электромагнитные волны.

Волновое уравнение

Уравнения Максвелла для вакуума при отсутствии токов (j = 0) и зарядов (r = 0) имеют следующий вид

,

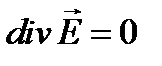
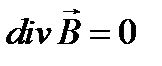
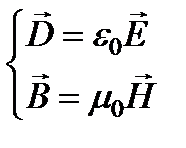где e ₀ и m ₀ – соответственно электрическая и магнитная постоянные. Уравнение показывает, что магнитное поле порождается переменным электрическим полем. Уравнение представляет собой математическую формулировку закона электромагнитной индукции. Следующее уравнение выражает факт отсутствия статического электрического поля в вакууме. Уравнение постулирует отсутствие магнитных зарядов. Применяя к обеим частям уравнения операцию rot, получаем

,

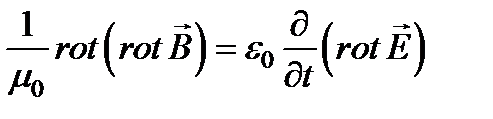где учтены соотношения и принято во внимание, что порядок дифференцирования по независимым переменным (пространственным координатам и времени) можно изменить. Применяя известное из векторного анализа соотношение для дифференциальных операторов, запишем

.

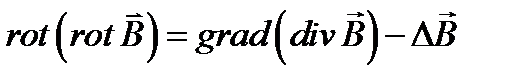Здесь D – оператор Лапласа, который в декартовых координатах записывается в виде

.

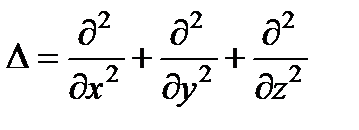Поскольку в рассмотренном случае 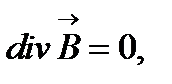то из соотношения с учетом уравнения получаем уравнение для вектора 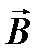: 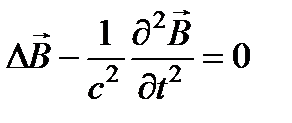, где 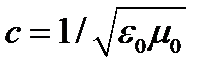– скорость света в вакууме. Аналогично, применяя операцию rot к обеим частям равенства, получим уравнение для вектора : .

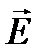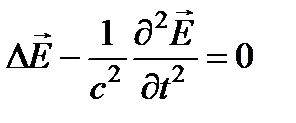Уравнения, линейны по полю. Поэтому они эквивалентны совокупности скалярных уравнений такого же вида, в каждое из которых входит только одна декартова компонента напряженности электрического или магнитного поле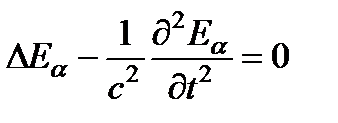й и 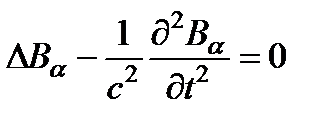(a = x, y, z).

Уравнения,, называются волновыми уравнениями. Их решения имеют характер распространяющихся волн.

Date: 2015-08-06; view: 402; Нарушение авторских прав