Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Плоская волна
|
|
Предположим, что произвольная компонента поля Ф (например, Еα или Вα) зависит лишь от одной пространственной координаты, например z, и времени, т.е. Ф = Ф(z, t). Тогда уравнение упростится и примет вид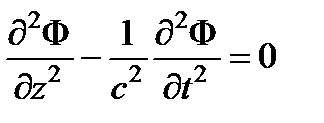 
. Уравнению удовлетворяет функция вида: 
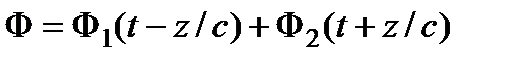, где Ф1 и Ф2 – произвольные (дифференцируемые) функции своих аргументов.
Формула выражает общее решение уравнения. Она описывает суперпозицию двух волн. Первая из них распространяется вдоль, а вторая – против оси z. Скорости обеих волн одинаковы и равны с. Действительно, возмущение Ф1, находившееся в момент времени t 1 в точке z 1, в момент t 2 приходит в точку z 2, определяемую соотношением t 1 – z 1/ c = t 2 – z 2/ c. Отсюда при t 2 > t 1 имеем z 2 > z 1, и скорость распространения волнового возмущения равна υ = (z 2 – z 1)/(t 2 – t 1) = c.
Функции Ф1 = Ф1(z, t) и Ф2 = Ф2(z, t) описывают плоские волны, так как волновое возмущение имеет одно и то же значение во всех точках бесконечной плоскости, перпендикулярной направлению распространения. Конкретный вид функций Ф1 и Ф2 определяется начальными и граничными условиями задачи.
Date: 2015-08-06; view: 350; Нарушение авторских прав