Сферическая волна

Нетрудно убедиться, что уравнениям удовлетворяют и волны вида

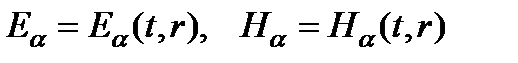, в которых напряженности полей зависят только от одной пространственной переменной – модуля радиус-вектора. 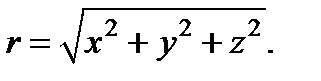Такие волны называют сферическими. Рассмотрим скалярное волновое уравнение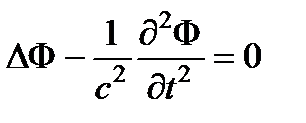

и будем искать его решение вида Ф = Ф(t, r). Для сферически симметричной функции Ф оператор Лапласа имеет вид 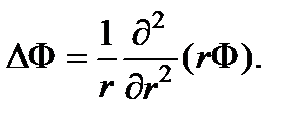Поэтому волновое уравнение перепишется следующим образом

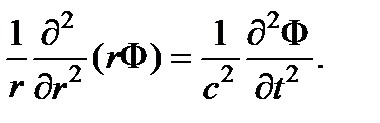
Введем вспомогательную функцию F = r Ф. Тогда последнее уравнение преобразуется к виду, аналогичному (1.10)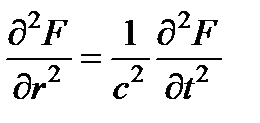

и, следовательно, его общее решение представится в виде суперпозиции двух волн, бегущих во взаимно противоположных направлениях

Возвращаясь к искомой функции Ф, получим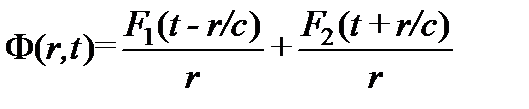

Выражение описывает две сферические волны. Первое слагаемое представляет собой волну, движущуюся в направлении увеличения значений r, т.е. от центра, где расположен точечный источник. Такая волна называется расходящейся. Второе слагаемое описывает волну, движущуюся в направлении уменьшения значения r, т.е. к центру. Такая волна называется сходящейся. Значение Ф в фиксированный момент времени на сфере постоянного радиуса является постоянным.

Date: 2015-08-06; view: 429; Нарушение авторских прав