Принцип суперпозиции

Согласно этому принципу световые волны разных частот и разных направлений распространяются в вакууме независимо друг от друга. Можно указать простые эксперименты, наглядно иллюстрирующие принцип суперпозиции. Так, через одно и то же отверстие в экране два наблюдателя могут видеть разные объекты.

Математически принцип суперпозиции является следствием линейности волнового уравнения, описывающего распространение световых волн в вакууме. В самом деле, если поля 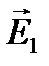, , 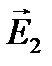… являются решениями волнового уравнения, то его решением оказывается и сумма полей 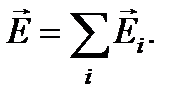В этом можно убедиться, подставляя, например, в волновое уравнение плоские волны вида .

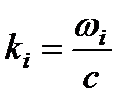При этом волновое уравнение распадается на независимые уравнения для отдельных волн.

Почти тривиальный в электромагнитной теории, принцип суперпозиции для сторонников корпускулярной теории света был непонятен, так как корпускулы, принадлежащие разным световым пучкам, должны как-то взаимодействовать, рассеиваться друг на друге.

Для световых волн, распространяющихся в материальной среде, современная лазерная оптика дает много примеров сильных нарушений принципа суперпозиции. С помощью лазеров получены громадные плотности потока энергии, порядка S ~ 10²⁰ Вт/м², что дает значение напряженности электрического поля световой волны, сравнимого с внутриатомными полями (E ~10⁹ В/м). Квантовая электродинамика предсказывает нарушение принципа суперпозиции для световых волн и в вакууме, но интенсивность которых очень большая даже по современным меркам. В очень мощных световых полях должно наблюдаться рассеяние света на свете и в вакууме.

Применяя принцип суперпозиции, можно показать, что две плоские монохроматические бегущие волны с одинаковой частотой, распространяющиеся в одном и том же направлении, в результате сложения дают также плоскую монохроматическую волну той же частоты, распространяющуюся в том же направлении. Если волны имеют разные частоты или различные направления распространения, то в результате их сложения не будет получена монохроматическая бегущая волна. Рассмотрим два примера.

Биения

Биения – периодические во времени изменения амплитуды колебания, возникающего при сложении двух гармонических колебаний с близкими частотами. Биения появляются вследствие того, что величина разности фаз между двумя колебаниями с различными частотами все время меняется так, что оба колебания оказываются в какой-либо момент времени в фазе, через некоторое время в противофазе и т.д. Соответственно амплитуда результирующего колебания периодически достигает то максимума, равного сумме амплитуд складываемых колебаний, то минимума, равного разности этих амплитуд (рис. 1.3).

Р и с. 1.3

При сложении двух бегущих в одном направлении волн с близкими частотами и волновыми числами биения возникают не только во времени, но и в пространстве.

Рассмотрим случай сложения двух монохроматических волн, имеющих частоты w ₁ и w ₂ и распространяющихся в одном направлении. Предположим, что векторы 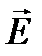в этих волнах коллинеарны. Для определенности ось Oz совместим с направлением распространения волн, а ось Ox совместим с направлением вектора 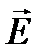волны, т.е. предположим, что 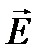(Е_x, 0, 0), а 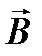(0, В_y, 0). Чтобы не загромождать изложения, будем следить за вектором 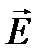, поскольку поведение вектора 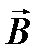определяется по вектору 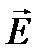с помощью соотношений между векторами плоской волны (правая тройка). Кроме того, предположим, что амплитуды напряженностей электрического поля слагаемых волн одинаковы:

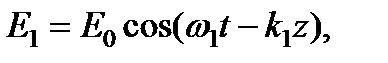
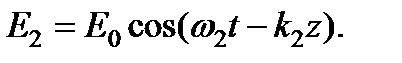В соответствии с принципом суперпозиции имеем: ,

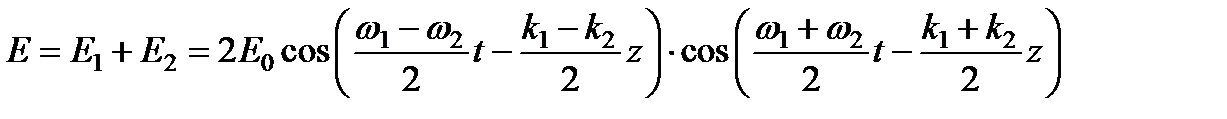где использована формула сложения косинусов. Учитывая, что k ₁ = w ₁/ c, k ₂ = w ₂/ c, представим в виде:

,

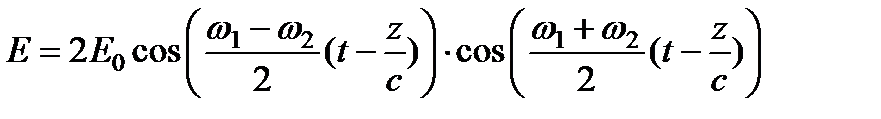который показывает, что результирующее электромагнитное поле распространяется без затухания в направлении положительных значений оси Oz со скоростью c (об этом свидетельствует наличие комбинации (t - z / c) в аргументе функции). В этом смысле речь идет о бегущей волне, однако не монохроматической. Учитывая, что в пределах оптического диапазона всегда соблюдается соотношение | w ₁ – w ₂| < < (w ₁ + w ₂) можно дать следующую наглядную интерпретацию такой волны: результирующая волна с частотой (w ₁ + w ₂)/2 и волновым числом (k ₁ + k ₂)/2, которые близки к частоте и волновому числу любой из компонент, имеют амплитуду, которая модулирована в пространстве и времени меняющейся огибающей с частотой (w ₁ -w ₂)/2 и волновым числом (k ₁ - k ₂)/2. На рис. 1.3 сплошной линией показаны колебания частоты (w ₁ + w ₂)/2, а пунктирной – огибающая амплитуды колебаний, изменяющейся от максимального значения 2 Е ₀ до нуля. Если амплитуды Е ₁₀ и Е ₂₀ полей слагаемых волн не равны друг другу, то амплитуда суммарной волны изменяется от (Е ₁₀ + Е ₂₀) до (Е ₁₀ – Е ₂₀). Частота биений равна разности частот складываемых компонент .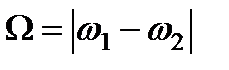

В результате интерференции при сложении двух волн с равными частотами и разными, но близкими по направлению волновыми векторами, биения возникают только в пространстве (так называемый муар). Именно такую структуру имеют волны во френелевской зоне излучателей, а также волны в различных волноводных системах.

Суперпозиция колебаний (или волн) с близкими частотами может возникнуть в нелинейных системах. Так, если на нелинейное устройство, например, квадратичный детектор, подать сумму двух колебаний, получим: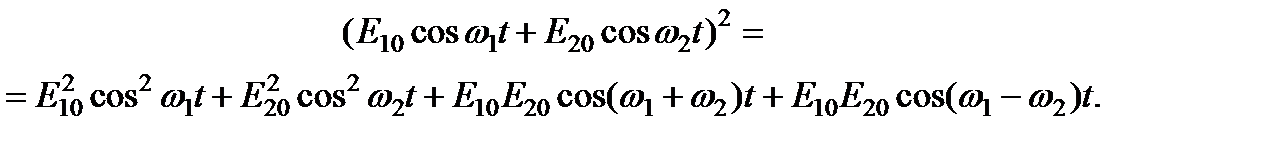

Последнее слагаемое – колебание с разностной частотой 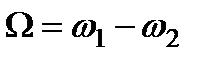– называется разностным тоном или тоном биений. Измерение тона биений лежит в основе точных измерений малых разностей двух близких частот, в частности сравнения некоторой измеряемой частоты с эталонной.

Date: 2015-08-06; view: 489; Нарушение авторских прав