Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Математическая модель изгиба
|
|
Изгиб это такой вид нагружения, когда внешние нагрузки направлены только перпендикулярно оси стержня. Математическая модель изгиба состоит из четырех дифференциальных уравнений:
,
,
,
,
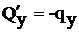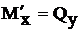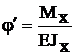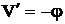где Qy – поперечная сила в сечении;
Мх– изгибающий момент в сечении;
qy – интенсивность внешних сил, направленных перпендикулярно оси стержня;
j – угол поворота сечения;
V – прогиб стержня, т.е. вертикальное перемещение сечения стержня;
Е – модуль Юнга материала, из которого выполнен стержня;
Jх – осевой момент инерции поперечного сечения стержня.
Решение данных дифференциальных уравнений имеет вид
Qy(z)= Qy(0) – ФQy,
Мх(z)= Мх(0) + Qy(0)×z – ФМ,
j(z)= j(0) + Мх(0)×z/EJx + Qy(0)×z2/2EJx – Фj,
V(z)= V(0) – j(0)z – Мx(0)×z2/2EJx– Qy(0)×z3/6EJx+ ФV,
где Qy(0) – поперечная сила, действующая в сечении с координатой z=0;
Мх(0) – изгибающий момент, действующий в сечении с координатой z=0;
j(0) – угол поворота сечения с координатой z=0,
V(0) – вертикальное перемещение сечения с координатой z=0,
ФQy – нагрузочная функция поперечной силы, зависящая от внешних сил, приложенных к стержню;
ФМ – нагрузочная функция изгибающего момента, зависящая от внешних сил, приложенных к стержню;
Фj – нагрузочная функция углов поворота, зависящая от внешних сил, приложенных к стержню;
ФV – нагрузочная функция прогибов, зависящая от внешних сил, приложенных к стержню.
Значения нагрузочных функций зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.
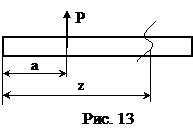
а) сосредоточенная сила (рис.13):
при z£a ФQ(z)=0, ФМ(z)=0, Фj(z)=0, ФV(z)=0;
при z³a ФQ(z)=P, ФМ(z)=P(z-a), Фj(z)=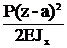 
, ФV(z)= 
.
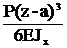б) начало распределенной нагрузки (рис.14):
при z£c ФQ(z)=0, ФМ(z)=0, Фj(z)=0, ФV(z)=0;
при z³c ФQ(z)=q(z-c), ФМ(z)=q(z-c)2/2, Фj(z)=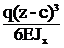 
, ФV(z)= 
.
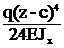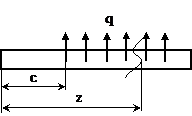
Рис. 14
в) окончание распределенной нагрузки, т.е. распределенная нагрузка заканчивается раньше чем стержень (рис.15):
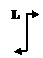
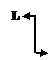
при z£d ФQ(z)=q(z-c), ФМ(z)=q(z-c)2/2, Фj(z)= 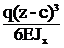, ФV(z)= ;
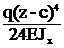при z³d ФQ(z)=q(z-c) – q(z-d), ФМ(z)=q(z-c)2/2 – q(z-d)2/2,
Фj(z)= –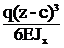 
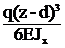, ФV(z)= – 
.
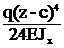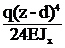Рис. 15
в) сосредоточенный момент (рис.16):
при z£b ФQ(z)=0, ФМ(z)=0, Фj(z)=0, ФV(z)=0;
при z³b ФQ(z)=0, ФМ(z)=L, Фj(z)=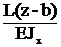 
, ФV(z)= 
.
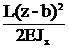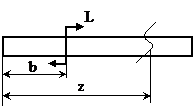
Рис. 16
Для определения силы, момента и перемещений в нулевом сечении используют граничные условия, которые приведены в таблице:
Табл. 3
| Левый конец стержня | Правый конец стержня длиною l | ||
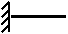
| V(0)=0; j(0)=0 | 
| V(l)=0; j(l)=0 |
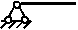
| V(0)=0; Mx(0)=0 |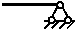 
| V(l)=0; Mx(l)=0 |
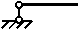
| V(0)=0; Mx(0)=0 |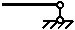 
| V(l)=0; Mx(l)=0 |
 
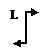
| Qy(0)=0; Mx(0)=0 |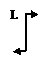  
| Qy(l)=0; Mx(l)=0 |
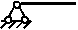
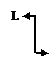
| V(0)=0;Mx(0)=–L |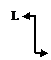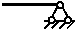 
| V(l)=0;Mx(l)=L |
|
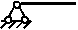
| V(0)=0; Mx(0)=L |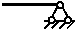
| V(l)=0;Mx(l)=–L |
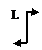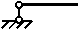
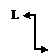
| V(0)=0;Mx(0)=–L |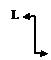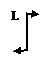   
| V(l)=0;Mx(l)=L |
|
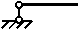
| V(0)=0; Mx(0)=L | 
| V(l)=0;Mx(l)=–L |
| Qy(0)=–P;Mx(0)=0 | 
| Qy(l)=P; Mx(l)=0 |
| Qy(0)=P; Mx(0)=0 |  
| Qy(l)= –P; Mx(l)=0 |
| Qy(0)=0;Mx(0)=–L | 
| Qy(l)=0;Mx(l)=L |
| Qy(0)=0; Mx(0)=L |
| Qy(l)=0; Mx(l)=–L |
Date: 2015-07-27; view: 1045; Нарушение авторских прав