Пример оформления решения по РГР I семестра. 1. Записать уравнение продольной силы N(z), граничные условия задачи, рассчитать значение продольной силы по участкам

ЗАДАЧА 1.1 Растяжение – сжатие.

Дано:

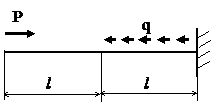
	P, кН	q, кН/м	l, м

Требуется:

1. Записать уравнение продольной силы N(z), граничные условия задачи, рассчитать значение продольной силы по участкам.

2. Выполнить чертёж схемы и эпюру в масштабе. Определить опасное сечение.

3. Из условия прочности подобрать размер прямоугольного поперечного сечения с соотношением высоты к основанию h: b =2:1, приняв допускаемое напряжение [σ]=160 МПа. Полученные значения округлить до нормального ряда чисел.

4. Для стержня выбранного размера вычислить нормальные напряжения в опасном сечении.

Решение:

Совместим начало координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.

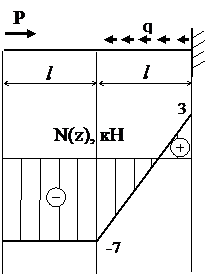В соответствии со схемой нагружения разделим стержень на 2 участка и запишем уравнение продольных сил:

N(z)=N(0)│_I + q(z- l)│_II

Г.У.: N(0)= – Р.

Построение графика продольных сил осуществляется по участкам.

I уч. 0 ≤ z ≤ l,

N(0)=N(l)=-7 кН.

II уч. l ≤ z ≤ 2 l

N(l)=N(0) + q(l - l)=-7 кН;

N(2 l)=N(0) + q(2 l - l)=3 кН.

Опасное сечение z=0, N_max=7 кН

По условию прочности: σ_max ≤ [σ], где σ_max=N_max/F и F=bh=2b², получаем:

b_пр= 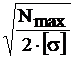= =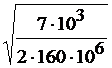0,00467 м →5 мм

h=2·b=2·5=10 мм.

Нормальные напряжения в опасном сечении для выбранного поперечного сечения будут равны: σ_z= 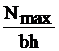= =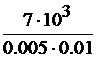140 МПа.

ЗАДАЧА 1.2 Кручение.

Дано:

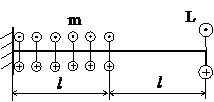
	L, кН·м	m, кН·м/м	l, м

Требуется:

1. Записать уравнение крутящего момента M_к(z), граничные условия задачи, рассчитать значение крутящего момента по участкам.

2. Выполнить чертёж схемы и эпюру в масштабе. Определить опасное сечение.

3. Из условия прочности подобрать размеры круглого d_кр и кольцевого поперечного сечения вала при отношении диаметров D:d=2:1, приняв допускаемое напряжение [τ]=90 МПа. Сравнить веса выбранных стержней.

Решение:

Совместим начало координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.

В соответствии со схемой нагружения разделим стержень на 2 участка и запишем уравнение крутящего момента:

M_к(z)=M_к(0) – mz│_I + m(z- l)│_II

Г.У.: M_к(2 l) = L.

M_к(2 l)=M_к(0) – 2m l + m(2 l - l)=L,

M_к(0)= m l+ L=20 кН·м.

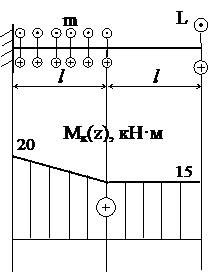
Построение графика крутящего момента осуществляется по участкам.

I уч. 0 ≤ z ≤ l,

M_к(0)=20 кН·м;

M_к(l)= M_к(0) – m l =15 кН·м.

II уч. l ≤ z ≤ 2 l

M_к(l)= M_к(0) – m l =15 кН·м.

M_к(2 l)= M_к(0) – 2m l + m(2 l - l)=15 кН·м.

Опасное сечение z=0, M _{к max}=20 кН·м.

По условию прочности: τ_max ≤ [τ], где τ_max= M _{к max}/W_ρ, где W_ρ – полярный момент сопротивления.

Для круглого сечения W_ρ=0.2d³_кр.

Таким образом, d_кр= 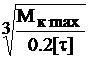= =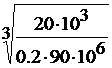0,1035 м → 104 мм.

Для кольцевого сечения W_ρ=0.2D³(1–1/2⁴) и D:d=2:1.

Значит, D= 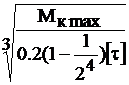= =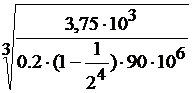0,1058 м → 106 мм,

d=D/2=106/2=53 мм → 52 мм.

Массу выбранных стержней оценим по их площадям:

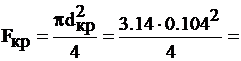0,0084 м² 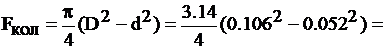0,0067 м².

Т.к. F_кр>F_кол, следовательно, m_кр>m_кол.

ЗАДАЧА 1.3 Поперечный изгиб.

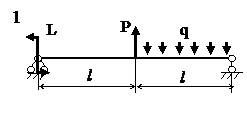
	P, кН	q, кН/м	L, кН·м	l, м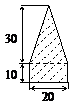

Дано:

Требуется:

1. Определить положение центра тяжести заданного поперечного сечения. Рассчитать центральные осевые моменты инерции. Выполнить чертёж сечения в масштабе, указать основные размеры, расстояния, положения осей.

2. Записать уравнение поперечной силы Q_y(z), изгибающего момента M_x(z) и граничные условия задачи. Рассчитать значения Q_y и M_х по участкам.

2. Выполнить чертёж схемы и эпюры в масштабе. Определить опасное сечение.

3. Записать уравнение и построить нулевую линию в опасном сечении. Вычислить напряжение в опасных точках данного сечения. Построить эпюру нормальных напряжений в опасном сечении.

4. Проверить сечение по условию прочности, приняв допускаемое напряжение [σ]=160 МПа.

1. Определить положение центра тяжести заданного поперечного сечения. Рассчитать центральные осевые моменты инерции. Выполнить чертёж сечения в масштабе, указать основные размеры, положение осей.

2. Записать уравнение поперечной силы Q_y(z), изгибающего момента M_x(z) и граничные условия задачи. Рассчитать значения поперечной силы и изгибающего момента по участкам.

3. Выполнить чертёж схемы и эпюр в масштабе. Определить опасное сечение.

4. Проверить сечение по условию прочности, приняв допускаемое напряжение [σ]=160 МПа.

Решение:

Рассчитываем необходимые значения для фигур № 1 и № 2, составляющих поперечное сечение:

Фигура № 1

Треугольник

F₁= 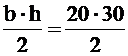=300 см²

J_x1= 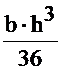= 15000 см⁴

J_y1= 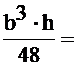5000 см⁴

Фигура № 2

Прямоугольник

F₂=b·h=20·10=200 см²

J_x2= 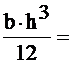1666,7 см⁴

J_y2= 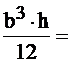6666,7 см⁴

Для определения положения центра тяжести сечения выбираем вспомогательные оси ХY.

x_c 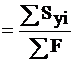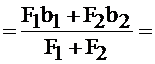10 см;

y_c 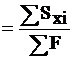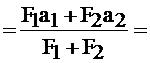14 см,

где а₁, а₂– расстояния между осью Х и осями Х₁ и Х₂ и равны а₁ = 20 см, а₂ = 5 см; а b₁, b₂ – расстояния между осями Y и осью Y₁, Y₂ соответственно, b₁= b₂ = 10 см.

Отмеряя в осях Х и Y координаты (х_с; y_c) находим положение центра тяжести всего сечения. Для определения центральных осевых моментов используем формулы преобразования при параллельном переносе осей:

J_xc= 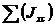= (J_x1 + (a₁ – y_c)²F₁) + (J_x2 + (a₂ – y_c)²F₂) =43666,7 см⁴

J_yc= 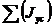= (J_y1 + (b₁ – x_c)²F₁) + (J_y2 + (b₂ – x_c)²F₂) =11666,7 см⁴

На схеме нагружения совместим начало координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.

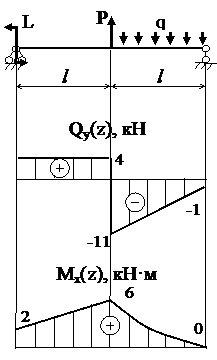В соответствии со схемой нагружения разделим стержень на 2 участка и запишем уравнения поперечной силы и изгибающего момента:

Q_y(z)=Q_y(0)│_I – Р + q(z- l)│_II

M_x(z)= M_x(0) + Q_y(0)z│_I – P(z- l) + q(z- l)²/2│_II

Г.У.: M_x(0) = L, M_x(2 l) =0.

M_x(2 l) =L + 2Q_y(0) l – P(2 l - l) + q(2 l - l)²/2=0,

Q_y(0)=(– L + P l – q l ²/2)/2 l =4 кН·м.

Построение графиков поперечной силы и изгибающего момента осуществляется по участкам.

I уч. 0 ≤ z ≤ l

Q_y(0)= Q_y(l)= 4 кН;

M_x(0)=L=2 кН·м;

M_x(l)= M_к(0) + Q_y(0) l =6 кН·м.

II уч. l ≤ z ≤ 2 l

Q_y(l)= Q_y(0) – Р + q(l - l)=-11 кН;

Q_y(2 l)= Q_y(0) – Р + q(2 l - l)=-1 кН·м.

M_x(l)= M_x(0)+Q_y(0) l – P(l - l) + q(l - l)²/2=6 кН·м;

M_x(2 l)=M_x(0)+Q_y(0) l –P(2 l - l)+q(2 l - l)²/2=0.

Опасное сечение z=0, M_{x max}= 6 кН·м.

Координаты крайних точек опасного поперечного сечения будут равны: у_А=26 см, у_В=-14 см.

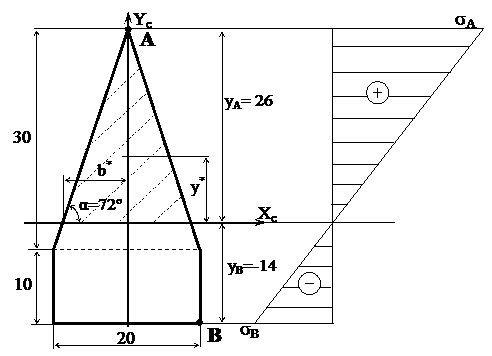
Нормальные напряжения в этих точках определим по следующим формулам: 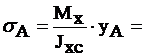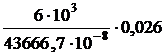=0,35 МПа

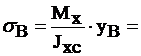
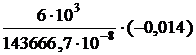= -0,19 МПа

Касательные напряжения в сечении, где Q_ymax определяются по формуле Журавского: 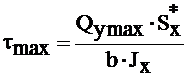=0,28 МПа,

где Q_{y max} – максимальная поперечная сила, Q_{y max} =-11 кН;

b – ширина отсекаемой части, b=2·b^*=17,3 см;

J_х – главный центральный момент инерции, J_хс= 43666,7 см⁴;

S_х^* – статический момент отсекаемой части, определяется из чертежа сечения по формуле:

S_х^* = F^*·y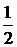^*= ( y_A·2b^*)·y^* = (y_A· 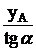)· 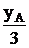= 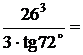1952,9 см³.

ЗАДАЧА 1.4 Изгиб с кручением.

Дано:

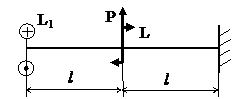
	P, кН	L, кН·м	L1, кН·м	l, м

Требуется:

1. Записать уравнение поперечной силы Q_y(z), изгибающего момента M_x(z), крутящего момента М_к(z) и граничные условия задачи. Рассчитать значения поперечной силы, изгибающего и крутящего моментов по участкам.

2. Выполнить чертёж схемы и эпюр в масштабе. Определить опасное сечение.

3. Подобрать размер круглого сечения из условия прочности, приняв допускаемое напряжение [σ]=160 МПа.

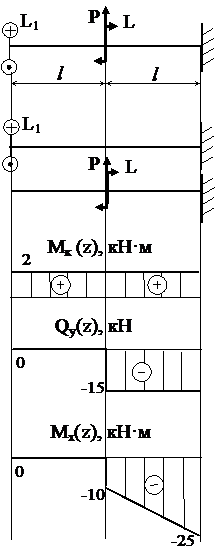Решение:

На схеме нагружения совместим начало координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.

Разделим исходную схему нагружения на две: кручение и поперечный изгиб. Запишем уравнение крутящего момента:

M_к(z)= M_к (0)│_{I, II}

Запишем уравнения поперечной силы и изгибающего момента:

Q_y(z)=Q_y(0)│_I – Р│_II

M_x(z)= M_x(0) + Q_y(0)z│_I – P(z- l) – L│_II

Г.У.: M_к(0)= L₁, Q_y(0) =0, M_x(0) =0.

Построение графиков осуществляется по участкам.

I уч. 0 ≤ z ≤ l,

M_к(0)=2 кН·м;

Q_y(0)= Q_y(l)= 0 кН;

M_x(0)=0 кН·м;

M_x(l)= M_к(0) + Q_y(0) l =0 кН·м.

II уч. l ≤ z ≤ 2 l

M_к(l)= M_к(2 l)=2 кН·м;

Q_y(l)= Q_y(2 l)= Q_y(0) – Р=-15 кН;

M_x(l)= M_x(0)+Q_y(0) l – P(l - l) – L =-10 кН·м;

M_x(2 l)=M_x(0)+Q_y(0) l –P_2y(2 l - l) – L =-25 кН·м.

Опасное сечение z=2 l, M_кmax=2кН·м, M_xmax= -25 кН·м.

Поскольку в опасной точке стержня будет двухосное напряженное состояние, то условие прочности запишем в виде:s_экв£[s]. По теории наибольших касательных напряжений: s_экв = s₁ - s₃.

В опасной точке поперечного сечения:

s_{z max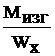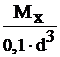} = = , t = = .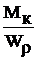

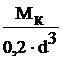Главные напряжения в этой точке: s_1,3 = 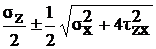, s₂ = 0. Тогда: s_экв = 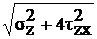= 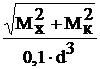£ [s], откуда

d ³ 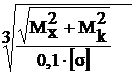= = 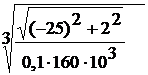0,1161 м = 116 мм.

Окончательно выбираем d=118 мм.

Date: 2015-07-27; view: 1694; Нарушение авторских прав