Понятия о напряжениях

В сечении выберем произвольную точку, а в её окрестности элементарную площадку DF. Равнодействующую сил, действующих на площадку, обозначим DР (рис.5).

Рис.5

Среднее полное напряжение на заданной площадке будет равно:

Р_ср = 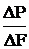. (4.1)

Если площадку уменьшать, то в пределе она обратится в точку. Напряжение – это предел отношения внутренней силы к площади, на которой она действует при условии, что площадь стремится к нулю. Р – полное напряжение [Н/м²] или [Па].

P = lim_DF®0 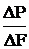. (4.2)

Иначе напряжение можно назвать интенсивностью внутренних сил по сечению.

Вектор полного напряжения можно разложить на проекции (рис.6). Проекцию полного напряжения на нормаль к плоскости сечения называется нормальным напряжением (обозначается s), а проекцию полного напряжения на плоскость сечения – касательным напряжением (обозначается t).

Р = 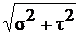(4.2)

Вектор нормали к сечению обозначим через вектор n.

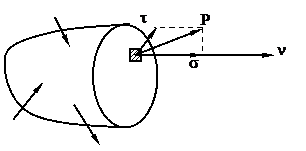Рис.6

Нормальные напряжения в плоскости поперечного сечения вычисляются по формуле:

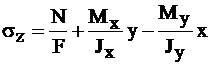, (4.3)

где s – нормальное напряжение в точке сечения;

N – продольная сила в сечении;

М_х, М_у – изгибающие моменты в сечении;

F – площадь поперечного сечения;

I_х, I_у – главные осевые моменты инерции сечения;

х, у – координаты точки, в которой вычисляется напряжение относительно главных центральных осей.

Касательные напряжения в плоскости поперечного сечения при кручении вычисляются по формуле:

t = 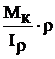, (4.4)

где t – касательное напряжение в точке сечения;

М_к – крутящий момент в сечении;

I_r – полярный момент инерции сечения;

r – расстояние от центра тяжести сечения до точки, в которой вычисляется касательное напряжение.

Касательное напряжение в плоскости поперечного сечения при изгибе вычисляются по формуле Журавского:

t = 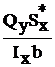, (4.5)

где t – касательное напряжение в точке сечения;

Q_у – поперечная сила в сечении;

I_х – осевой момент инерции относительно главной оси Х;

b – ширина сечения на том уровне, где вычисляются напряжения;

S 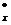– статический момент части сечения отсеченной по уровню на котором вычисляются напряжения относительно главной оси Х.

Date: 2015-07-27; view: 609; Нарушение авторских прав