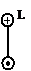Математическая модель кручения. Кручение это такой вид нагружения, когда все внешние нагрузки лежат в плоскостях поперечных сечений

Кручение это такой вид нагружения, когда все внешние нагрузки лежат в плоскостях поперечных сечений, но их линии действия не проходят через ось стержня. Математическая модель кручения состоит из двух дифференциальных уравнений:

,

,

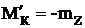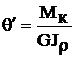где М_к– крутящий момент в сечении;

m_z – интенсивность внешнего момента, направленного вокруг оси стержня;

Q – угол закрутки, т.е. перемещение сечения стержня вокруг оси стержня;

G – модуль сдвига материала, из которого выполнен стержня;

J_r – полярный момент инерции поперечного сечения стержня.

Решение данных дифференциальных уравнений имеет вид

М_к(z)= М_к(0) – Ф_Мк,

Q(z)= Q(0)+ М_к(0)/GJ_r – Ф_Q,

где М_к(0) – крутящий момент, действующий в сечении с координатой z=0;

Q(0) – угол закрутки сечения с координатой z=0;

Ф_Мк – нагрузочная функция крутящего момента, зависящая от внешних моментов, приложенных к стержню;

Ф_Q – нагрузочная функция углов закрутки, зависящая от внешних моментов, приложенных к стержню.

Значения нагрузочных функций зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенный момент (рис.10):

при z£a Ф_м(z)=0, Ф_q(z)=0,

при z³a Ф_м(z)=L, Ф_q(z)= .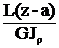

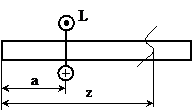
Рис. 10

б) начало распределенной нагрузки (рис.11):

при z£c Ф_м(z)=0, Ф_q(z)=0;

при z³c Ф_м(z)=m(z-c), Ф_q(z)= .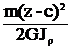

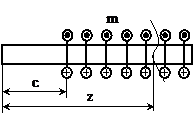
Рис. 11

в) окончание распределенной нагрузки, т.е. распределенная нагрузка заканчивается раньше чем стержень (рис.12):

при z£d Ф_м(z)=m(z-c), Ф_q(z)= ;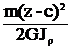

при z³d Ф_м(z)=m(z-c) – m(z-d), Ф_q(z)= – .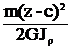

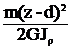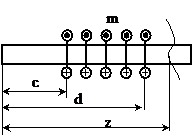
Рис. 12

Для определения момента и перемещения в нулевом сечении используют граничные условия, которые приведены в таблице:

Табл.2

Левый конец стержня	Правый конец стержня длиною l
	Q(0)=0		Q(l)=0
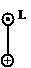
	Мк(0)=0		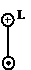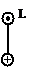Мк(l)=0
	Мк(0)= –L		Мк(l)=L
	Мк(0)=L		Мк(l)= –L

Date: 2015-07-27; view: 527; Нарушение авторских прав