Геометрические характеристики плоских фигур. При решении задач возникает необходимость оперировать некоторыми геометрическими (интегральными) характеристиками плоских сечений (ихс)

При решении задач возникает необходимость оперировать некоторыми геометрическими (интегральными) характеристиками плоских сечений (ИХС). Эти характеристики имеют применение, в основном, при решении задач на прочность и жесткость и в силу узкого прикладного значения их рассматривают в курсе «Сопротивления материалов».

Статическими моментами площади сечения относительно осей Х и Y называются определённые интегралы вида

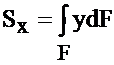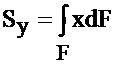, , (3.1)

где F – площадь сечения, dF – её элемент, а x и y – координаты этого элемента.

Статические моменты могут быть любого знака и имеют размерность [м³].

Оси, проходящие через центр тяжести сечения, называются центральными. Статические моменты относительно центральных осей равны нулю.

Координаты центра тяжести сечения x_c и y_c, составленного из нескольких простых фигур (i – индекс фигуры), определяются соотношениями:

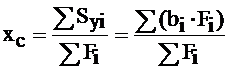, (3.2)

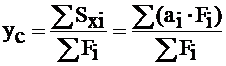, (3.3)

где а_i – расстояние между вспомогательной осью Х и центральной осью i -той фигуры Х_i,

b_i – расстояние между вспомогательной осью Y и центральной осью i -той фигуры Y_i,

F_i – площадь i-той фигуры.

Осевыми моментами инерции площади сечения относительно осей Х и Y называются определённые интегралы вида

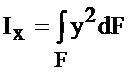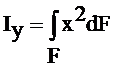, (3.4)

Осевые моменты инерции могут быть только положительными и имеют размерность – [м⁴].

Центробежным моментом инерции площади сечения относительно осей Х и Y называется определённый интеграл вида

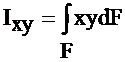(3.5)

Центробежный момент инерции может быть любого знака и имеет размерность – [м⁴].

Моменты инерции относительно центральных осей, параллельных вспомогательным вычисляются по формулам:

,

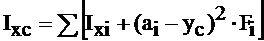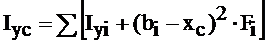, (3.6)

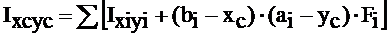
где 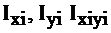– моменты инерции i -той фигуры относительно собственных центральных осей, параллельных вспомогательным осям.

Главные оси, т.е. две взаимно перпендикулярные оси, относительно которых центробежный момент инерции сечения равен нулю; занимают положение, определяющееся уравнением:

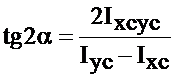, (3.7)

где α – угол, на который необходимо повернуть оси, чтобы они стали главными.

Главные моменты инерции, т.е. осевые моменты инерции, вычисленные относительно главных осей инерции, определяются следующими выражениями:

J_x0=J_xс·cos²α + J_yс·sin²α – J_xcyс·sin2α, (3.8)

J_y0=J_yс·cos²α + J_xс·sin²α + J_xcyс·sin2α. (3.9)

Свойство моментов инерции: сумма осеых моменто инерции при повороте не меняется

J_x0 + J_y0=J_xс + J_yс (3.10)

Полярным моментом инерции площади сечения называется определённый интеграл вида

I_r= 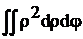= = 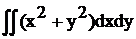I_х+ I_у (3.11)

Полярный момент инерции может быть только положительным и имеет размерность – [м⁴].

Осевые моменты сопротивления площади сечения относительно осей Х и Y называются выражения вида

W_х= 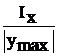, W_у= 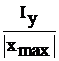. (3.12)

Осевые моменты сопротивления могут быть только положительными и имеют размерность – [м³].

Полярный момент сопротивления площади сечения называется выражение вида

W_r= 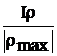. (3.13)

Полярный момент сопротивления может быть только положительным и имеет размерность – [м³].

Date: 2015-07-27; view: 374; Нарушение авторских прав