Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример оформления решения по РГР II семестра. 1. Записать уравнение продольной силы N(z) и продольного перемещения W(z), граничные условия задачи
|
|
ЗАДАЧА 2.1 Растяжение – сжатие.
Дано:
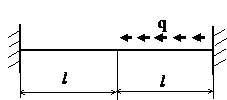
| q, кН/м | l, м |
Требуется:
1. Записать уравнение продольной силы N(z) и продольного перемещения W(z), граничные условия задачи, рассчитать значение продольной силы и продольного перемещения по участкам.
2. Выполнить чертёж схемы и эпюр в масштабе. Определить опасное сечение.
3. Из условий прочности и жёсткости подобрать размер квадратного поперечного сечения, приняв допускаемое напряжение [σ]=160 МПа и допускаемое перемещение [W]=0,002· l.
Решение:
Совместим начало координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.
В соответствии со схемой нагружения разделим стержень на 2 участка и запишем уравнения продольных сил и линейных перемещений:
N(z)=N(0)│I + q(z- l)│II
W(z)=W(0) + N(0)z/EF│I + q(z- l)2/2EF│II
Г.У.: W(0)=0, W(2 l)=0 → N(0)= – 2.5 кН
Построение графиков осуществляется по участкам.
I уч. 0 ≤ z ≤ l,
N(0)=N(l)=-2,5 кН,
W(0)=0, W(l)=-2,5/EF.
II уч. l ≤ z ≤ 2 l
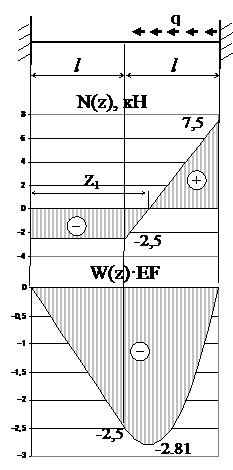 N(l)=-2,5 кН; N(2 l)=7,5кН.
N(l)=-2,5 кН; N(2 l)=7,5кН.
W(l)=-2,5/EF, W(2 l)=0.
Исследование на экстремум:
N(0) + q(z1- l)=0, → z1=1.25 м
W(z1)=W(0)+N(0)z1/EF+q(z1- l)2/2EF=-2,81/EF
Условие прочности: опасное сечение z=2 l. σmax ≤ [σ], где σmax=Nmax/F. Таким образом, F =Nmax/[σ],а с учетом, что F= a2, получаем
апр= 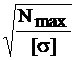 =
= 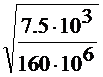 =0,0068 м → 8 мм
=0,0068 м → 8 мм
Условие жёсткости: опасное сечение z=z1. Wmax ≤[W]. С эпюры линейных перемещений 2,81/(EF)=[W], откуда F= 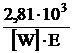 =а2, т.е. значит
=а2, т.е. значит
аж= 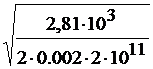 =0,0018 м → 2 мм
=0,0018 м → 2 мм
Окончательно выбираем сечение, удовлетворяющее условиям прочности и жёсткости: а=8 мм.
ЗАДАЧА 2.2 Кручение.
Дано:
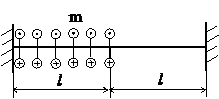
| m, кН·м/м | l, м |
Требуется:
1. Записать уравнение крутящего момента Mк(z) и угла закрутки Q(z), граничные условия задачи, рассчитать значение крутящего момента и угла закрутки по участкам.
2. Выполнить чертёж схемы и эпюр в масштабе. Определить опасное сечение.
3. Из условий прочности и жёсткости подобрать круглое поперечное сечение, приняв допускаемое напряжение [τ]=90 МПа и допускаемый угол закрутки [Q]= 0,002· l.
Решение:
Совместим начало координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.
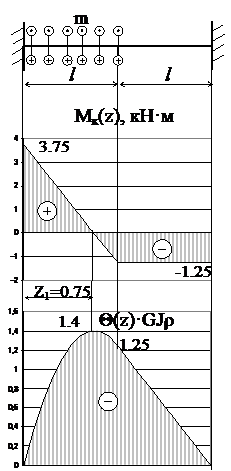 В соответствии со схемой нагружения разделим стержень на 2 участка и запишем уравнения крутящего момента и углов закрутки:
В соответствии со схемой нагружения разделим стержень на 2 участка и запишем уравнения крутящего момента и углов закрутки:
Mк(z)=Mк(0) – mz│I + m(z- l)│II
Θ(z)=Θ(0) + Mк(0)z/GJρ – mz2/2GJρ│I + m(z- l)2/2GJρ│II
Г.У.: Θ(0)=0,Θ(2 l)=0 → Mк(0)=3.75 кН·м.
Построение графиков осуществляется по участкам.
I уч. 0 ≤ z ≤ l,
Mк(0)=3.75кН·м, Mк(l)=-1.25кН·м.
Θ (0)=0, Θ(l)=1.25/GJρ.
II уч. l ≤ z ≤ 2 l
Mк(l)=-1.25 кН·м; Mк(2 l)=-1.25 кН·м.
Θ(l)=1.25/GJρ, Θ(2 l)=0.
Исследование на экстремум:
Mк(0) – mz1=0, → z1=0.75 м
Θ(z1)= Mк(0)z1/GJρ + m(z1- l)2/2GJρ =1.4/GJρ
Условие прочности: опасное сечение z=0. τmax ≤ [τ], где τmax= M к max/Wρ, где полярный момент сопротивления для круглого сечения определяется по формуле Wρ=0.2d3 .Таким образом,
dпр=  =
=  =0,059 м → 60 мм
=0,059 м → 60 мм
Условие жёсткости: опасное сечение z=z1. Θmax ≤ [Θ], где Θmax=1.4/GJρ, где для кольцевого сечения полярный момент инерции Jρ=0.1d4. Таким образом,
dж= 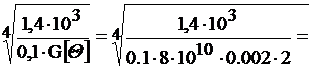 0,081 м → 82 мм
0,081 м → 82 мм
Окончательно выбираем сечение, удовлетворяющее условиям прочности и жёсткости: d=82 мм.
ЗАДАЧА 2.3 Поперечный изгиб.
Дано:

| P, кН | L, кН·м | q, кН/м | l, м | 
|
 Требуется:
Требуется:
1. Записать уравнение поперечной силы Qy(z), изгибающего момента Mx(z), угла поворота φ(z), вертикального перемещения V(z) и граничные условия задачи. Рассчитать значения Qy, Mх, φ и V по участкам.
2. Выполнить чертёж схемы и эпюры в масштабе (при необходимости исследовать на экстремум).
3. Из условий прочности и жёсткости подобрать указанное в исходных данных поперечное сечение, приняв допускаемое напряжение [σ]=160 МПа и допускаемый прогиб [V]=0,002· l.
Решение:
Совместим начало координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.
В соответствии со схемой нагружения разделим стержень на 2 участка и запишем уравнения поперечной силы, изгибающего момента, угла поворота и прогиба:
Qy(z)=Qy(0)│I – Р + q(z- l)│II
Mx(z)= Mx(0) + Qy(0)z│I – P(z- l) + q(z- l)2/2│II
φ(z)=φ(0) + Mx(0)z/EJx + Qy(0)z2/2EJx│I –
– P(z- l)2/2EJx + q(z- l)3/6EJx│II
V(z)=V(0) – φ(0)z – Mx(0)z2/2EJx –
–Qy(0)z3/6EJx│I + P(z- l)3/6EJx – q(z- l)4/24EJx│II
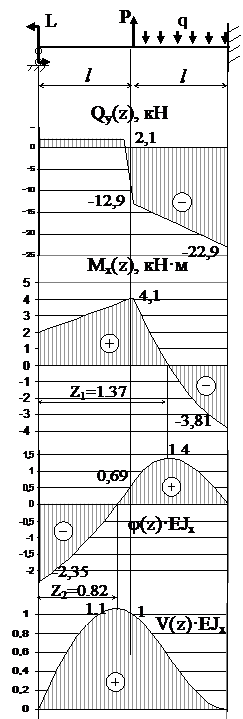
Г.У.: Mx(0)=L, Mx(2 l)=0, V(0)=0, V(2 l)=0 → Qy(0)=2.1 кН, φ(0)=-2.35/EJx
Построение графиков осуществляется по участкам.
I уч. 0 ≤ z ≤ l,
Qy(0)=2.1 кН, Qy(l)=2.1 кН.
Mx(0)=2 кН·м, Mx(l)=4.1 кН·м.
φ(0)=-2.35/EJx, φ(l)=-0.69/EJx.
V(0)=0, V(l)=1/EJx.
II уч. l ≤ z ≤ 2 l.
Qy(l)=-12.9 кН, Qy(2 l)=22.9 кН.
Mx(l)=4.1 кН·м, Mx(2 l)=-3.18 кН·м.
φ(l)=0.69/EJx, φ(2 l)=0.
V(l)=1/EJx, V(2 l)=0.
Исследование на экстремум:
1. Mx(z1)= Mx(0) + Qy(0)z1 – P(z1- l) + q(z1- l)2/2=0, → z1=1,37 м
φ(z1)=φ(0)+Mx(0)z1/EJx+ Qy(0)z12/2EJx– P(z1- l)2/2EJx + q(z1- l)3/6EJx=1,4/EJx.
2. φ(z2)=φ(0) + Mx(0)z2/EJx + Qy(0)z22/2EJx=0, → z2=0.82 м
V(z)=V(0) – φ(0)z2 – Mx(0)z22/2EJx – Qy(0)z23/6EJx=1,1/EJx.
По условию прочности: опасное сечение z= l. σmax≤ [σ], где σmax= 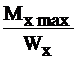 . Таким образом, Wx=
. Таким образом, Wx= 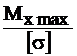 =
= 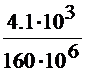 =0,0000255 м3 → 26 см3.
=0,0000255 м3 → 26 см3.
Из таблиц сортамента выберем двутавр № 10 (Wx= 39,7 см3).
По условию жёсткости: опасное сечение z=z2. Vmax≤[V]. С эпюры линейных перемещений 1,1·103/(EJx)=[V], откуда
Jx= 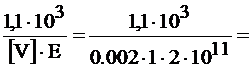 0,00000275 м3 → 275 см4 .
0,00000275 м3 → 275 см4 .
Из таблиц сортамента выберем двутавр № 12 (Jx= 350 см3).
Окончательно выбираем сечение, удовлетворяющее условиям прочности и жёсткости: двутавр № 12.
ЗАДАЧА 2.4 Криволинейный стержень.
Дано:

| Р, кН | α | R = l, м |
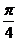
|
Требуется:
1. Записать уравнение продольной силы N(z), поперечной силы Qy(z), изгибающего момента Mx(z), и граничные условия задачи. Рассчитать значения Qy, Mх, N по участкам.
2. Выполнить чертёж схемы и эпюры в масштабе.
3. Подобрать круглое поперечное сечение стержня из расчета на прочность по изгибающему моменту, приняв допускаемое напряжение [σ]=160 МПа.
Решение:
Уравнение изгибающего момента:
Mx(φ)= Mx(0) + Qy(0)Rsinφ + N(0)R(1 – cosφ)│I – PR(1 – cos(φ – α))│II
Уравнение поперечных сил:
Qy(φ)=M'x/R = Qy(0)cosφ + N(0)sinφ│I – Psin(φ – α)│II
Уравнение продольных сил:
N(φ)=Q′y= – Qy(0)sinφ + N(0)cosφ│I – Pcos(φ – α)│II
Г.У.: Mx(0)=0, Qy(0)= P, N(0)=0
Построение графиков осуществляется по участкам:
I уч. 0 ≤ φ ≤ α
N(0)=0, N(α)=-19.8 кН.
Qy(0)=28 кН, Qy(α)=19.8 кН.
Mx(0)=0, Mx(α)=27.7 кН·м.
II уч. α ≤ φ ≤ π/2
N(α)=-47.8, N(α/2)=-47.8 кН.
Qy(α)=19.8 кН, Qy(α/2)=-19.8 кН.
Mx(α)=33.2 кН·м,Mx(α/2)=27.7 кН·м.
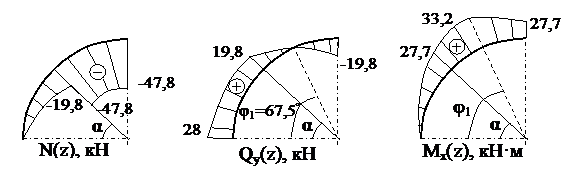 Исследование на экстремум:
Исследование на экстремум:
Qy(φ1)= Qy(0)cosφ1 – Psin(φ1 – α)=0, → φ1=67.5°
Mx(φ1)= Mx(0) + Qy(0)Rsinφ1 – PR(1 – cos(φ1 – α))=33.2 кН·м.
Расчёт на прочность произведём по максимальному изгибающему моменту: σmax=М х max/Wx ≤ [σ], где Wx – момент сопротивления сечения изгибу. Для круглого стержня Wx=0,1d3. Таким образом,
d= 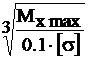 =
= 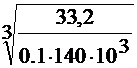 =0,1333 м
=0,1333 м
Из нормального ряда размеров выбираем значение d=134 мм
ЗАДАЧА 2.5 Рама.
Дано:
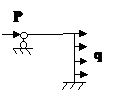
| Р, кН | q, кН/м | длина стержней, м |
Требуется:
1. Определить степень статической неопределимости рамы.
2. Определить значение реакции методом сил.
3. Записать уравнение поперечной силы Qy(z), изгибающего момента Mx(z), и граничные условия. Рассчитать значения Qy, Mх на каждом стержне рамы.
4. Выполнить чертёж схемы и эпюр в масштабе.
5. Подобрать квадратное поперечное сечения стержня из расчета на прочность по изгибающему моменту, приняв допускаемое напряжение [σ]=160 МПа.
Решение:
Данная система является статически неопределимой, поэтому сначала определим количество «лишних» связей: n=m – 3=4 – 3=1. Решать будем методом сил.
Система, нагруженная реальной силой:
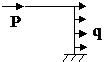 1 стержень: Qy1(z)= Qy1(0)
1 стержень: Qy1(z)= Qy1(0)
Mx1(z)= Mx1(0) + Qy1(0)z
2 стержень: Qy2(z)= Qy2(0) – qz
Mx2(z)= Mx2(0) + Qy2(0)z – qz2/2
Г.У.: Qy1(0)=0; Mx1(0)=0; Мх1(l)=Мх2(0), Qy2(0)= – P → Mx2(0)=0 кН·м.
Система, нагруженная единичной силой:
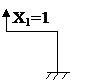 1 стержень: Q0y1(z)= Q0y1(0)
1 стержень: Q0y1(z)= Q0y1(0)
M0x1(z)= M0x1(0) + Q0y1(0)z
2 стержень: Q0y2(z)= Q0y2(0)
M0x2(z)= M0x2(0) + Q0y2(0)z
Г.У.: Q0y1(0)= – 1; M0x1(0)=0; М0х1(l)=М0х2(0), Qy2(0)=0 →
M0x1(z)= –z, M0x2(0)= – l
Запишем каноническое уравнение метода сил: Δ1Р + δ11·Х1=0. Перемещения определим по интегралу Мора.
Δ1Р= 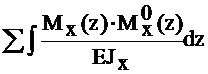 =
= 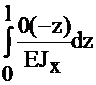 +
+ 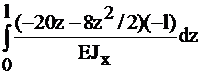 =
= 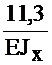 ;
;
δ11= 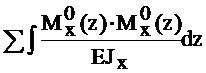 =
= 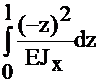 +
+ 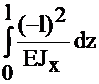 =
= 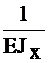 +
+ 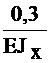 =
= 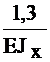 Из канонического уравнения определим: Х1=
Из канонического уравнения определим: Х1= 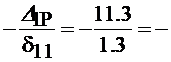 8,7 кН.
8,7 кН.
Запишем уравнения поперечных сил и изгибающих моментов для каждого стержня:
1 стержень: Qy1(z)= Qy1(0)
Mx1(z)= Mx1(0) + Qy1(0)z
2 стержень: Qy2(z)= Qy2(0) – qz
Mx2(z)= Mx2(0) + Qy2(0)z – qz2/2
Г.У. Mx1(0)=0
|
Qy2(0)= – Р Mx2(0)=8,7 кН·м
Mx1(l)= Mx2(0)
Построение эпюр осуществляется для каждого стержня в отдельности:
1 ст. 0 ≤ z ≤ l,
Qy1(0)=8,7 кН, Qy1(l)=8,7 кН.
Mx1(0)=0, Mx1(l)=8,7 кН·м.
2 ст. 0 ≤ z ≤ l,
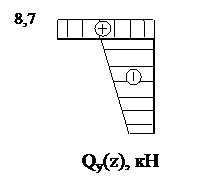
Qy2(0)=-20 кН, Qy2(l)=-12 кН.
Mx2(0)=8,7 кН·м, Mx2(l)=-15,3 кН·м.
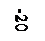
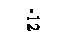
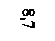
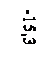
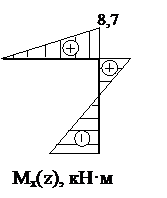
Расчёт на прочность: σmax=М х max/Wx ≤ [σ], где Wx=а3/6 – осевой момент сопротивления.
Таким образом, а= 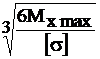 =
= 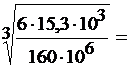 0,083 м=83 мм.
0,083 м=83 мм.
Из нормального ряда размеров выбираем значение а=84 мм
ВАРИАНТЫ ЗАДАНИЙ
Таблица исходных данных
Табл. 5
| № вар. | l, м | Р, кН | q, кН/м | L, кН·м | m, кН·м/м | L1, кН·м | r, мм | α,° (II сем.) | Сечение к задаче №3 (II сем.) |
| 0,5 | 
| ||||||||
| -6 | 
| ||||||||
| 0,5 | 
| ||||||||
| -2 | 
| ||||||||
| 0,5 | 
| ||||||||
| -3 | 
| ||||||||
| 0,5 | 
| ||||||||
| -4 | 
| ||||||||
| 0,5 | 
| ||||||||
| -5 | 
| ||||||||
| 0,5 | 
| ||||||||
| -6 | 
| ||||||||
| 0,5 | 
| ||||||||
| -8 |        
| ||||||||
| 0,5 | |||||||||
| -2 | |||||||||
| 0,5 | |||||||||
| -3 | |||||||||
| 0,5 | |||||||||
| -4 | |||||||||
| 0,5 | |||||||||
| -5 |         
| ||||||||
| 0,5 | |||||||||
| -6 | |||||||||
| 0,5 | |||||||||
| -8 | |||||||||
| 0,5 | |||||||||
| -2 | |||||||||
| 0,5 | |||||||||
| -3 |
Варианты заданий I семестра
Задача № 1.1
Табл. 6

|
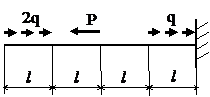
|
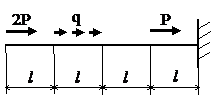
|
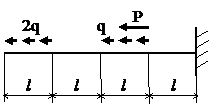
|
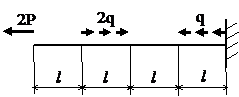
|
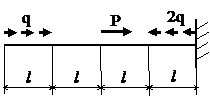
|
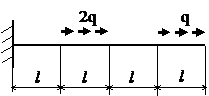
|
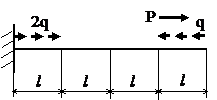
|
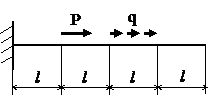
|
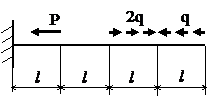
|
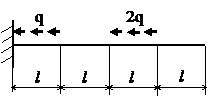
|
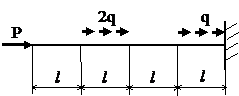
|
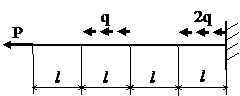
|
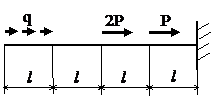
|
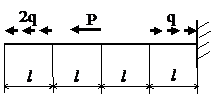
|

|
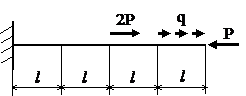
|

|
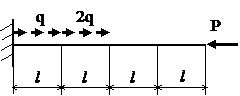
|
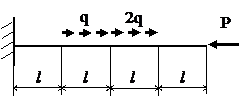
|
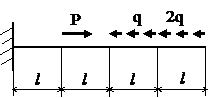
|
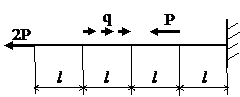
|
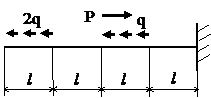
|
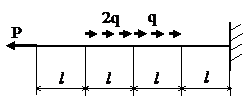
|
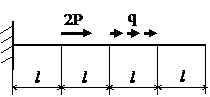
|
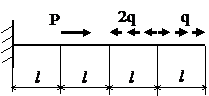
|
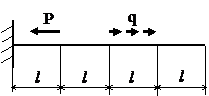
|
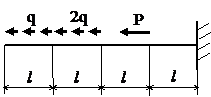
|
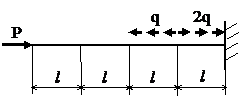
|
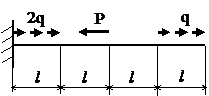
|
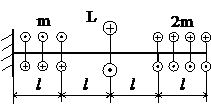
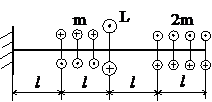
Задача № 1.2
Табл.7
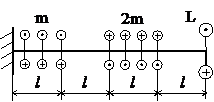
|
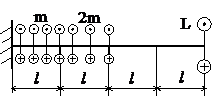
|
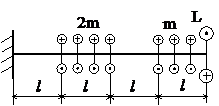
|
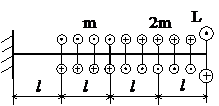
|
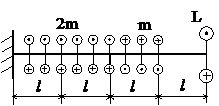
|
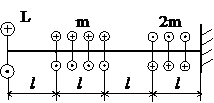
|
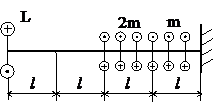
|
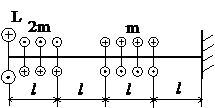
|
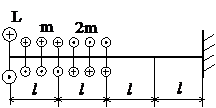
|
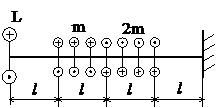
|
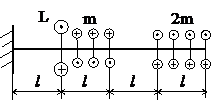
|
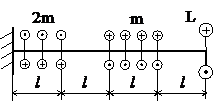
|
|
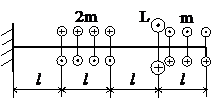
|
|
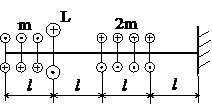
|
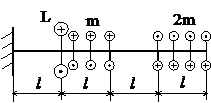
|
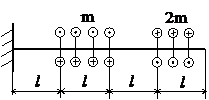
|
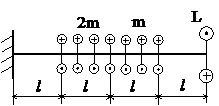
|
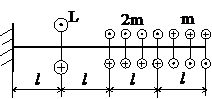
|
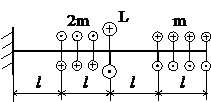
|
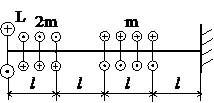
|
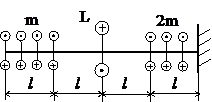
|
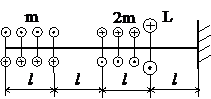
|
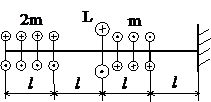
|
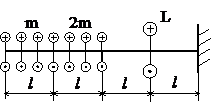
|
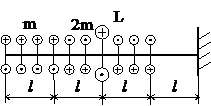
|
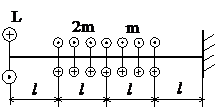
|
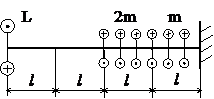
|
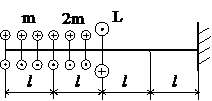
|
Задача № 1.3
Табл.8
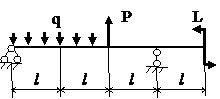
|
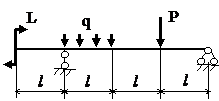
|
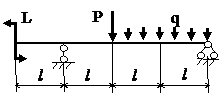
|
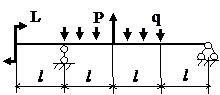
|
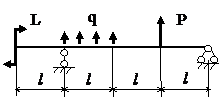
|
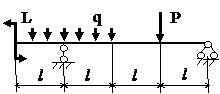
|
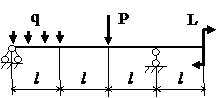
|
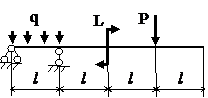
|
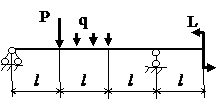
|
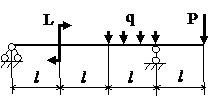
|
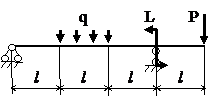
|
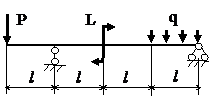
|
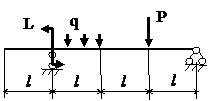
|
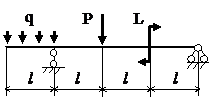
|
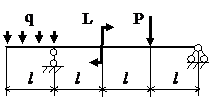
|
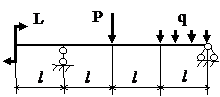
|
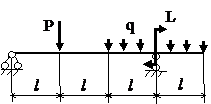
|
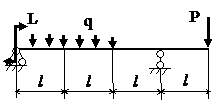
|
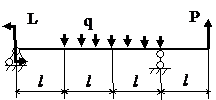
|
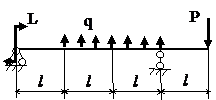
|
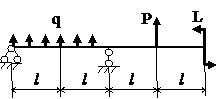
|
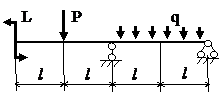
|
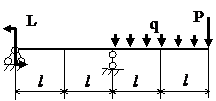
|
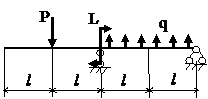
|
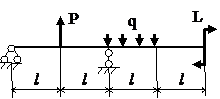
|
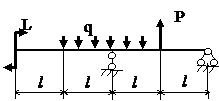
|
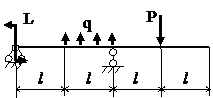
|
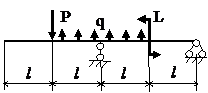
|
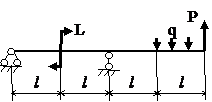
|
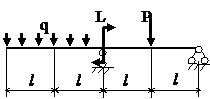
|
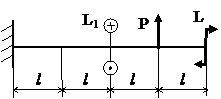
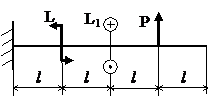
Задача № 1.4
Табл.9
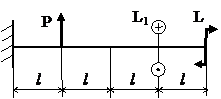
|
 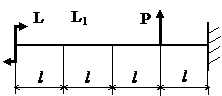
|
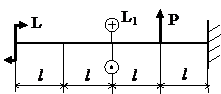
|
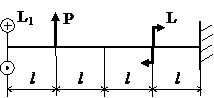
|
|
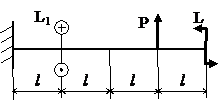
|
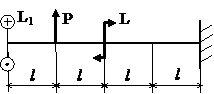
|
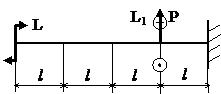
|
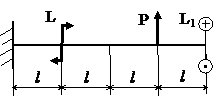
|

|
|
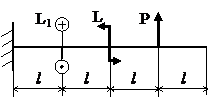
|
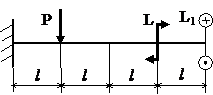
|
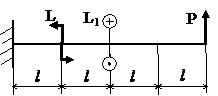
|
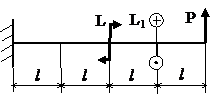
|
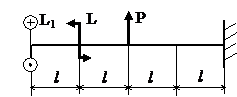
|
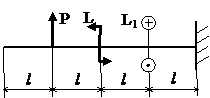
|
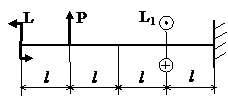
|
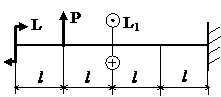
|
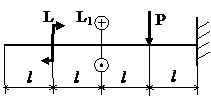
|
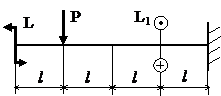
|
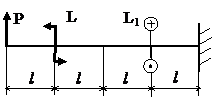
|
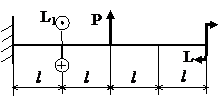
|
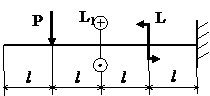
|
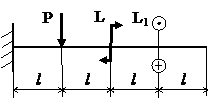
|
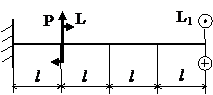
|
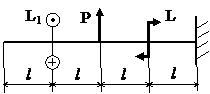
|
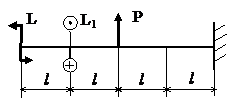
|
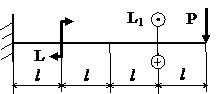
|
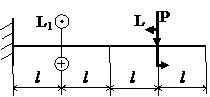
|
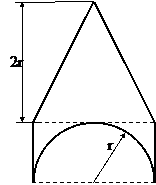
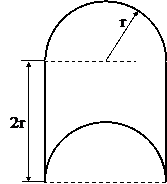
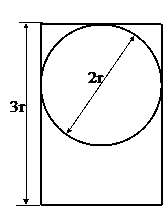
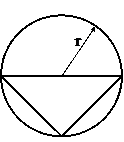
Поперечное сечение (к задаче №1.3)
Табл.10
|
|

| ||
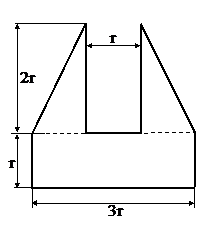
|

|
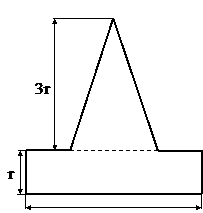
| ||

|

|

| ||
|

|

| ||
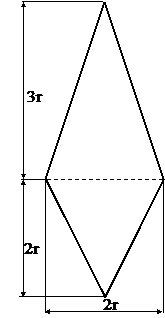
|

|
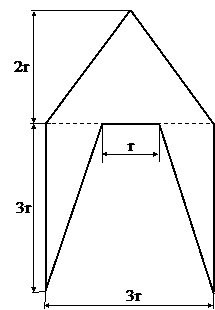
| ||
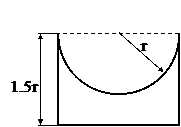
|
|
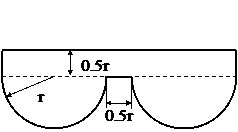
| ||

|
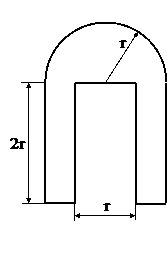
|

| ||

|

|
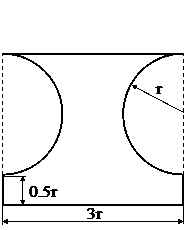
| ||

|

|

| ||

|

|

|
Варианты заданий II семестра
Задача № 2.1
Для получения схемы нагружения в задаче №1.1(табл.1) со стороны свободного конца добавить жёсткую заделку. В случае если на свободный конец действует сосредоточенная нагрузка, её следует убрать.
Задача № 2.2
Для получения схемы нагружения в задаче №1.2(табл.2) со стороны свободного конца добавить жёсткую заделку. В случае если на свободный конец действует сосредоточенная нагрузка, её следует убрать.
Задача № 2.3
Для получения схемы нагружения в задаче №1.3(табл.3) со стороны свободного конца добавить жёсткую заделку. В случае если на свободный конец действует сосредоточенная нагрузка, её следует убрать.
Задача № 2.4
Табл.11
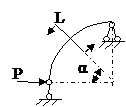 1 1
| 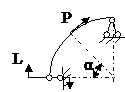 2 2
|
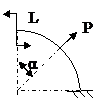
|
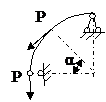 4 4
|  5 5
|

|
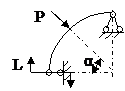 7 7
|
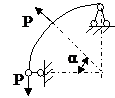
|
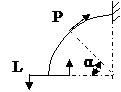
|
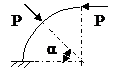 10 10
| 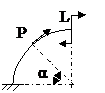 11 11
|
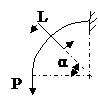
|
 13 13
| 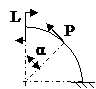 14 14
| 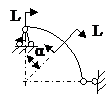 15 15
|
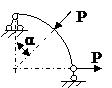 16 16
| 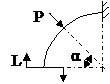 17 17
|
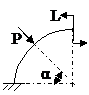
|
 19 19
| 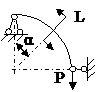 20 20
|
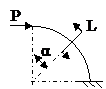
|
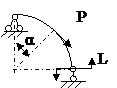 22 22
|
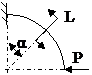
| 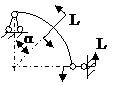 24 24
|
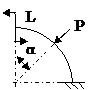 25 25
|
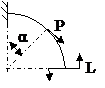
| 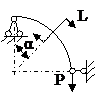 27 27
|
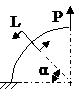
|
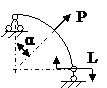
|
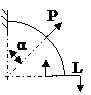
|
Задача № 2.5
Табл. 12
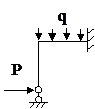 1 1
| 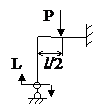 2 2
|
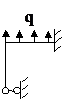
|
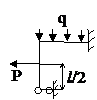
|
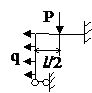
|
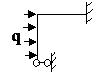
|
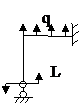
|
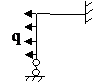
|
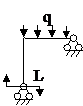
|
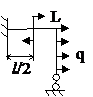
|
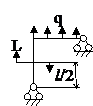
| 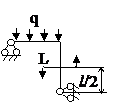 12 12
|
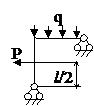
|
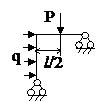
|
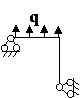
|
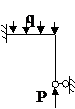
|
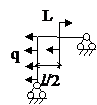
| 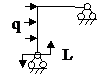 18 18
|
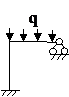
|
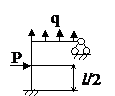
|
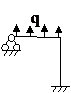
|
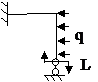
| 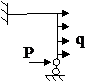 23 23
|
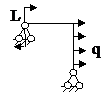
|
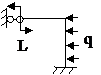 25 25
|
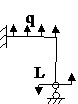
| 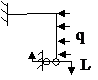 27 27
|
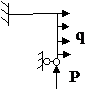
|  29 29
| 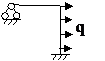 30 30
|
Date: 2015-07-27; view: 1397; Нарушение авторских прав