Метод наложения (суперпозиция) токов

Этот метод можно применять для определения токов в цепи, в которой одновременно действуют несколько ЭДС. Этот метод основан на принципе наложения и применим только для линейных цепей.

Сущность принципа наложения заключается в том, что ток в любой ветви цепи с постоянными сопротивлениями равен алгебраической сумме частичных токов, создаваемых в этой ветви каждой из ЭДС в отдельности.

Алгоритм расчёта:

1. Определим количество токов в цепи. Выбираем условно направление тока в каждой ветви.

а) Предложим, что в цепи действует только одна какая–либо ЭДС.

б) Все остальные ЭДС приравниваем к нулю.

в) Все сопротивления оставляем неизменённым, включая внутреннее сопротивления всех источников.

г) Получим цепь с последовательно–параллельным соединением сопротивлений.

д) Для такой схемы находим токораспределение. Указываем на схеме направления токов, вызванных действием только одной ЭДС. Это так называемые частичные токи. Обозначают их с одним штрихом: I'.

е) Зная сопротивления участков и ЭДС источника, используя закон Ома и соотношения величин при последовательном и параллельном соединении резисторов, определим значение частичных токов от одного источника ЭДС.

3. Аналогично полагаем, что в цепи действует вторая ЭДС, а все остальные не действуют. Повторяем расчёт частичных токов от действия второго источника, их обозначают с двумя штрихами: I″.

4. Аналогично производим расчёты поочерёдно для всех ЭДС схемы.

5. Определяем действительные значения токов в каждой ветви по принципу наложения токов, то есть, алгебраически сложив частичные токи, определяем действительные значения токов на каждом участке сложной цепи, когда все ЭДС действуют одновременно.

Правило алгебраического сложения токов:

Знак, который ставится перед частичным током при алгебраическом сложении, зависит от того, совпадает ли направление этого тока с выбранным направлением действительного тока в ветви или противоположно ему. Если совпадает, то знак «+», если противоположно, то знак «–».

Пример:

Дано: (Рис18) R₁=R₃=2 Ом; R₂=1,6 Ом; E₁=3,6 В; E₂=4,8 В; r₀₁=r₀₂=0,5 Ом.

Найти: все токи.

Решение задачи:

1. Применение метода наложения к цепи на рис.18.

Разветвление цепи с несколькими источниками энергии, включенными в разные ветви, к числу которых относится и цепь на рис. 18, являются сложными цепями. Для таких сложных электрических цепей существует ряд методов, один из которых (метод наложения) рассматривается в этом параграфе, а другие методы в следующих параграфах.

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частичных токов, созданных каждой ЭДС в отдельности. В нашем случае следует:

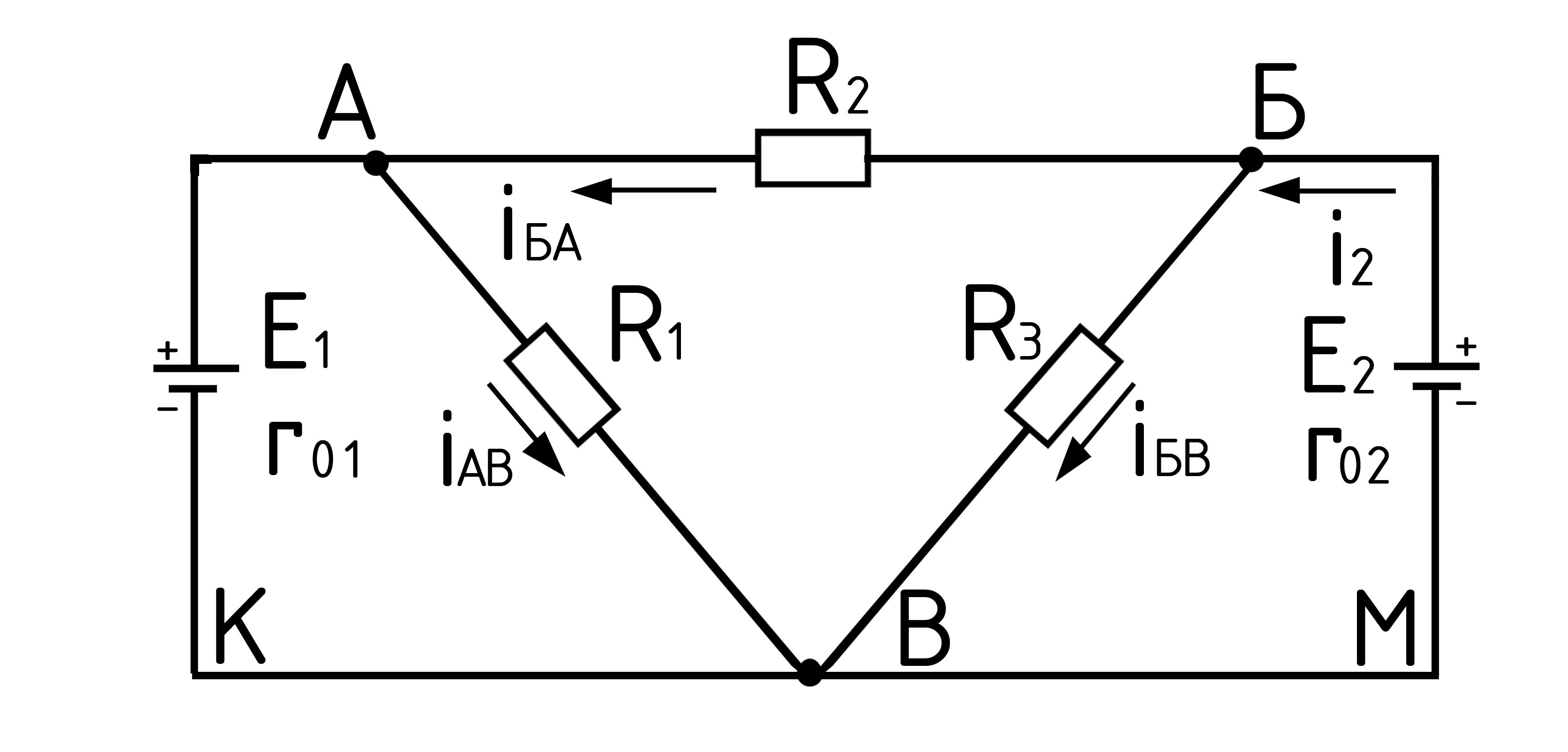
Рис. 18.

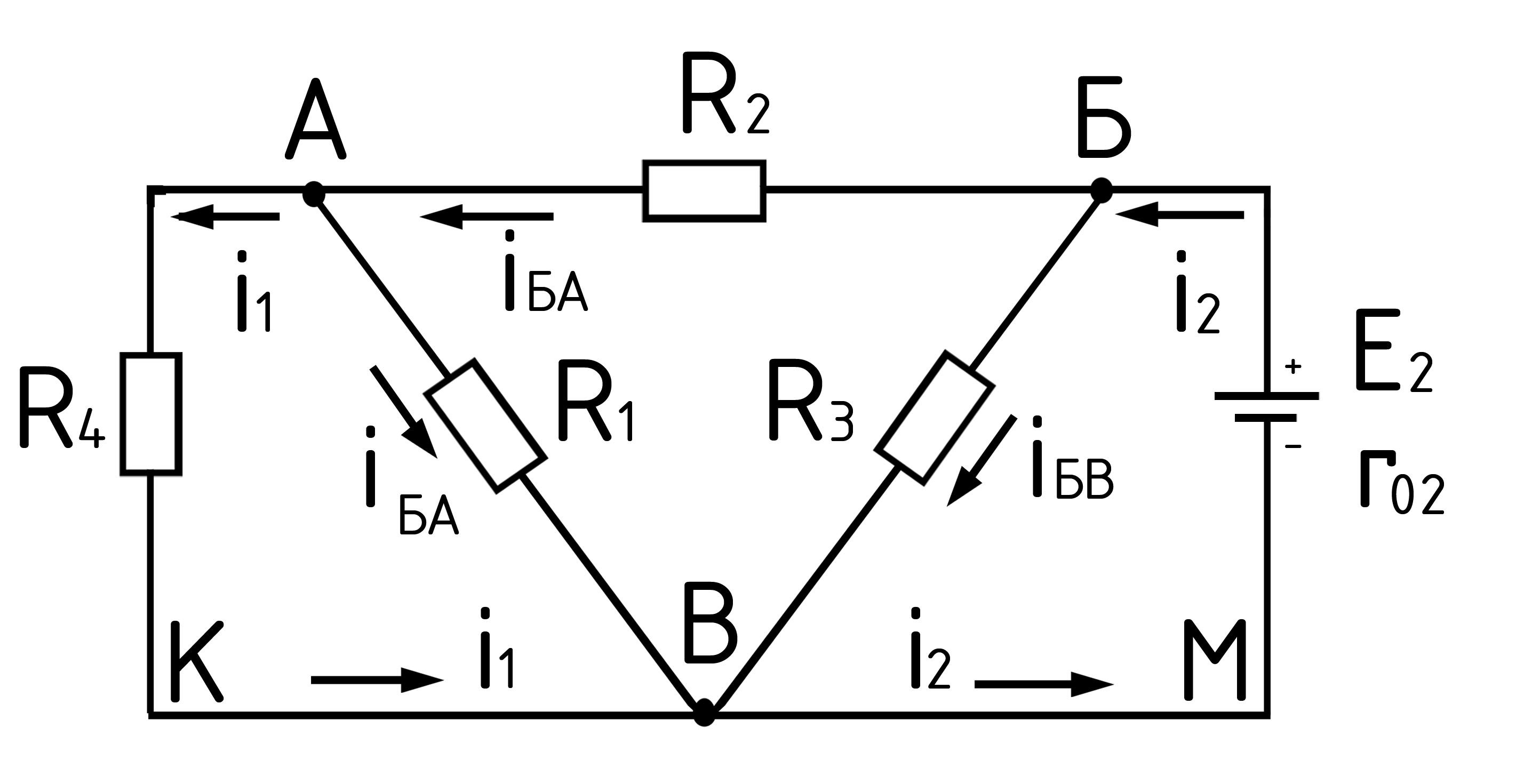
Рис. 19.

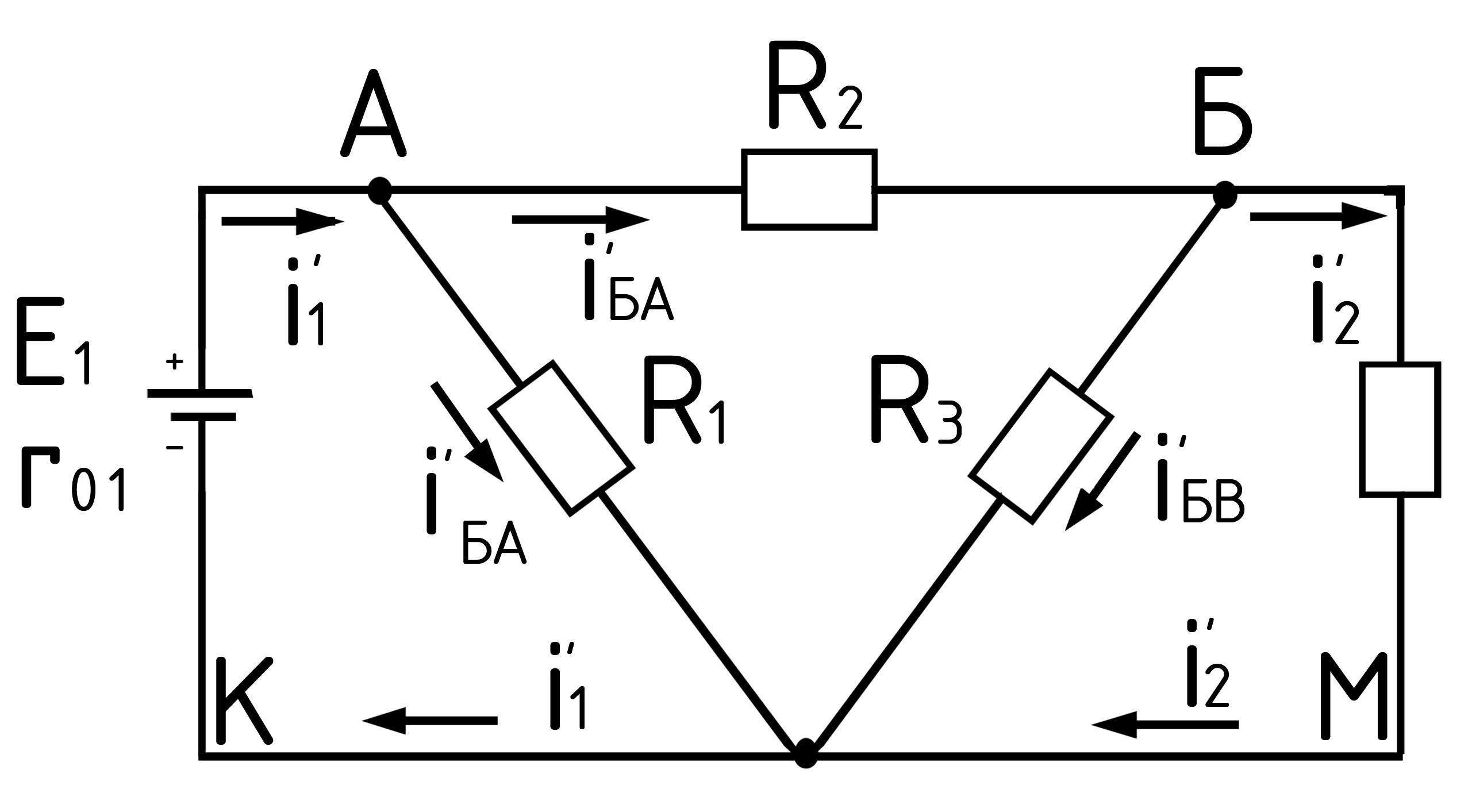
Рис. 20.

во-первых, определить частичные токи от ЭДС Е₁ при отсутствии ЭДС Е₂, т.е. рассчитать простую цепь по рис. 19; во-вторых найти частичные токи от ЭДС Е₂ при отсутствии ЭДС Е₁, т.е. рассчитать простую цепь по рис. 20; в-третьих, алгебраически сложить частичные токи двух последних схем.

Итак, метод наложения позволяет заменить расчёт одной сложной цепи с несколькими источниками энергии (рис. 18) расчётом нескольких в данном случае двух) цепей с одним источником энергии в каждой.

2. Обозначение частичных токов. Все частичные токи от ЭДС Е₁ (рис. 19.) обозначим буквой I с одним штрихом, а все частичные токи от ЭДС Е₂ (рис. 20.) – с двумя штрихами.

3. Вычисление частичных токов. Для цепи с ЭДС Е₁ (рис. 19.) рассчитаем сначала общее сопротивление. Сопротивление участка БВ

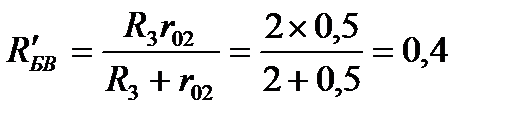Ом.

Оно соединено последовательно с сопротивлением R₂, поэтому

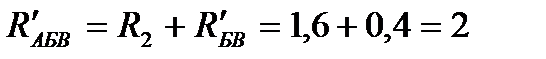Ом.

Два одинаковых сопротивления R'_АБВ R₁ соединены параллельно, поэтому общее сопротивление всей внешней цепи

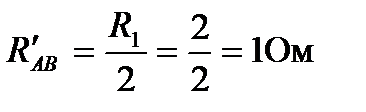
Ток источника

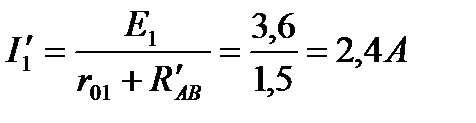
разветвляется в узловой точке А на два одинаковых тока:

Ток I'_АБ разветвляется в узловой точке Б на токи:

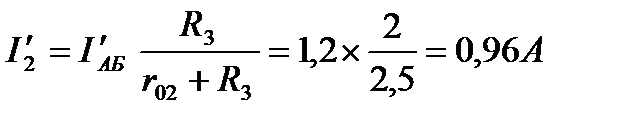
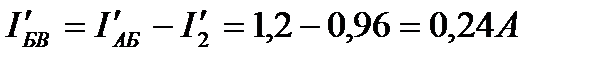
Для цепи с ЭДС E₂ (рис.20):

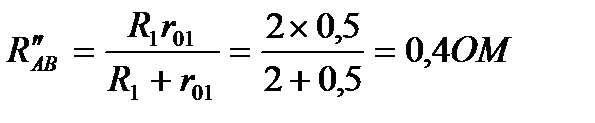
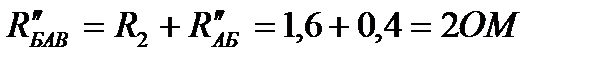
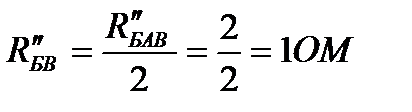
так как R₃=R″_БАВ.

В ветви источника с ЭДС E₂ ток

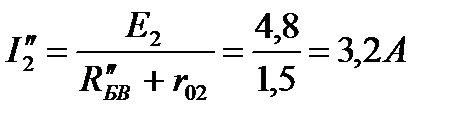
Поскольку R″_БАВ=R₃=2,0 Ом, то ток

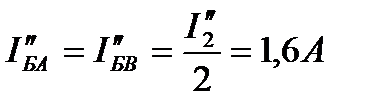
Токи в параллельных ветвях участка АВ:

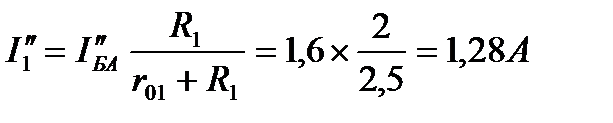
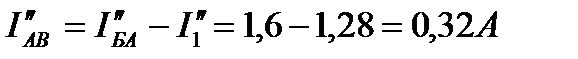
4. Вычисление токов в цепи на рис. 20. Выполним алгебраическое сложение частичных токов.

На участке ВКА частичный ток I'₁ (рис. 19) направлен от узла В к узлу А, а частичный ток I″₁ (рис. 20) – от А к В, т.е. навстречу первому. Поэтому суммарный ток

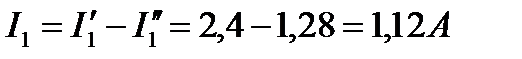
Направление тока I₁ (рис. 19.) совпадает с направлением большего частичного тока, т.е. тока I'₁.

Аналогичным образом определяем I_БА и I₂:

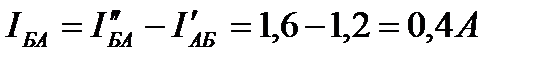
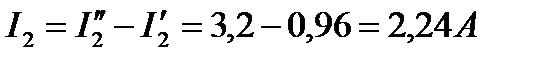
Направления токов I_БА и I₂ (рис.20) совпадают с направлениями токов I″_БА и I″₂ соответственно.

В ветви АВ оба частичных тока (I'_АБ и I″_АБ) совпадают по направлению, поэтому

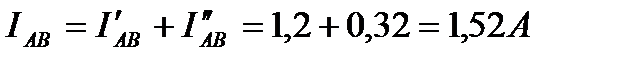
Аналогично

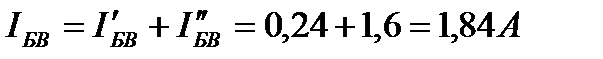
5. Вычисление напряжений. Напряжения между узловыми точками:

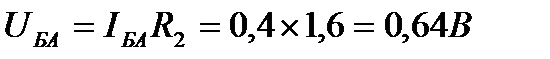
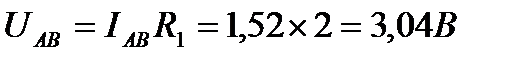
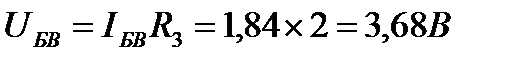
6. Проверка результатов вычислений. Для проверки расчётов составим уравнение по законам Кирхгофа.

Для узла А: 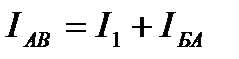; действительно, 1,52=1,12+0,4.

Для узла Б: 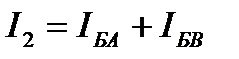; действительно, 2,24=0,4+1,84.

Для контура АВБ: 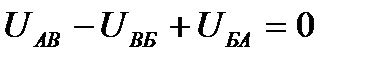; действительно, +3,04-3,68+0,64=0 (обходим против направления движения стрелки часов).

*Дополнительные вопросы к задаче

1. Как применяется метод наложения для расчёта цепей. содержащих более двух источников?

если сложная цепь содержит, например три источника ЭДС Е₁, Е₂ и Е₃, включенных в разные ветви, то следует составить три схемы для расчёта частичных токов: одна схема будет содержать только ЭДС Е₂, а третья – только ЭДС Е₃.

Рассчитав в трёх схемах частичные токи и алгебраически сложив их, получим токи заданной цепи.

2. В каких случаях для расчёта сложной цепи целесообразно применять метод наложения?

Наиболее трудоёмкой частью в расчётах по методу наложения является вычисление частичных токов. Поэтому его применяют при небольшом числе источников – при двух, иногда трёх.

Этот метод удобен также в тех случаях, когда не нужен полный расчёт цепи, а требуется найти, например, только токи в участках с источниками.

3. В каких случаях расчёт токов методом наложения может привести к большим погрешностям в результатах?

Если результирующий ток ветви выражается разностью двух близких величин, то незначительная относительная погрешность в определении слагаемых (частичных токов) может привести к весьма большой относительной погрешности результата (действительного тока ветви). В таких случаях метод наложения применять нецелесообразно.

Date: 2015-07-24; view: 5416; Нарушение авторских прав