
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Эквивалентное преобразование треугольника и звезды сопротивлений
|
|
Цепь с одним источником питания тоже может быть сложной, при наличии в ней соединений, называемых треугольником и звездой.
Треугольник сопротивлений называют соединения трёх ветвей, образующих замкнутый контур с тремя узлами (рис. 27 а)
а) б)
Рис. 27 а,б.
Звездой сопротивлений называют соединение трёх ветвей, имеющих общий узел (рис. 27, б)
Расчёт цепи может быть упрощен, если соединения треугольником преобразовать в звезду или наоборот. Такое преобразование можно производить лишь в том случае, когда обе схемы равнозначны (эквивалентны).
Эквивалентными можно считать схемы, у которых потенциалы узлов и токи, подходящие к узлам, постоянны, а, следовательно, постоянны полные сопротивления между соответствующими узлами.
Для вывода выражений, связывающих сопротивления таких эквивалентных схем, предположим, что ток в одном из подводящих проводов равен нулю.
Предположим ток IЛ=0, тогда сопротивления между узлами В и С в треугольнике и между В и С в звезде равны, то есть
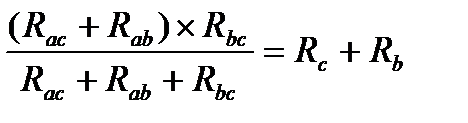
при токе IB=0 сопротивления между узлами А и С в данных соединениях равны
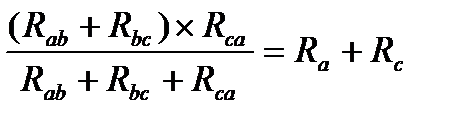
при токе IC=0 сопротивления между узлами А и В в обоих случаях равны:
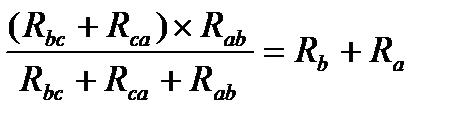
Допустим, что преобразуется треугольник в звезду. Тогда сопротивления сторон треугольника Rab Rbc Rca следует считать заданными. Необходимо определить сопротивления лучей звезды Rb, Ra, Rc. Решая систему уравнений (1), (2), (3) найдём искомые сопротивления:
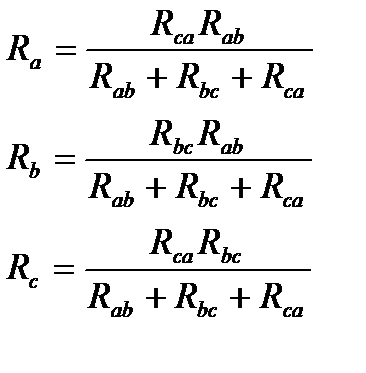
Для запоминания этих формул существует правило:
Каждое сопротивление эквивалентной звезды равно отношению произведения двух примыкающих к соответствующему узлу сопротивлений треугольника к сумме трёх его сопротивлений.
Если преобразовывать звезду в треугольник, то заданными следует считать сопротивления лучей звезды Rb Ra Rc. Сопротивления сторон треугольника Rab Rbc Rca следует определить.
Решая совместно уравнения (1),(2),(3) найдём искомые сопротивления:
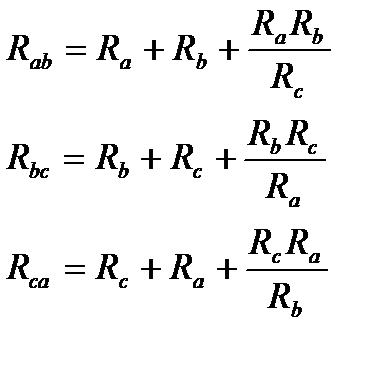
Мнемоническое правило для запоминания формул перехода:
Сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем её узлам, что и сторона треугольника, и их произведения, делённого на сопротивление третьего луча звезды.
Если сопротивления лучей звезды равны друг другу: Rb=Ra=Rc (что практически бывает часто), то будут равны друг другу и сопротивления сторон треугольника, то есть Rab=Rbc=Rca, причём из формул получается простые соотношения:
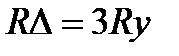 или
или 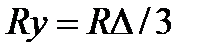
следовательно, сопротивления ветви симметричного треугольника в три раза больше сопротивления ветви симметричной звезды и наоборот.
В большинстве случаев расчёт сложной цепи значительно упрощается, если треугольник сопротивлений заменить звездой сопротивлений.
Алгоритм расчёта сложной цепи методом преобразования треугольника сопротивлений в эквивалентную звезду:
1. Определить количество неизвестных токов и укажем их направление.
-Любой треугольник сопротивлений можно заменить эквивалентной звездой.
-В результате замены получается другая схема, позволяющая упростить расчёт.
-Найдём сопротивления лучевой звезды.
-Найдём полное сопротивление упрощённой цепи.
-Зная ЭДС источника и полное сопротивление цепи по закону Ома, найдём ток в неразветвлённой части схемы.
-Найдём напряжение на параллельном участке.
-Найдём токи исходной электрической цепи, найдём по законам Кирхгофа. Составим уравнения по двум законам Кирхгофа для неизвестных токов.
2.7 Расчет цепи с применением метода преобразования «треугольника» сопротивлений в «звезду»
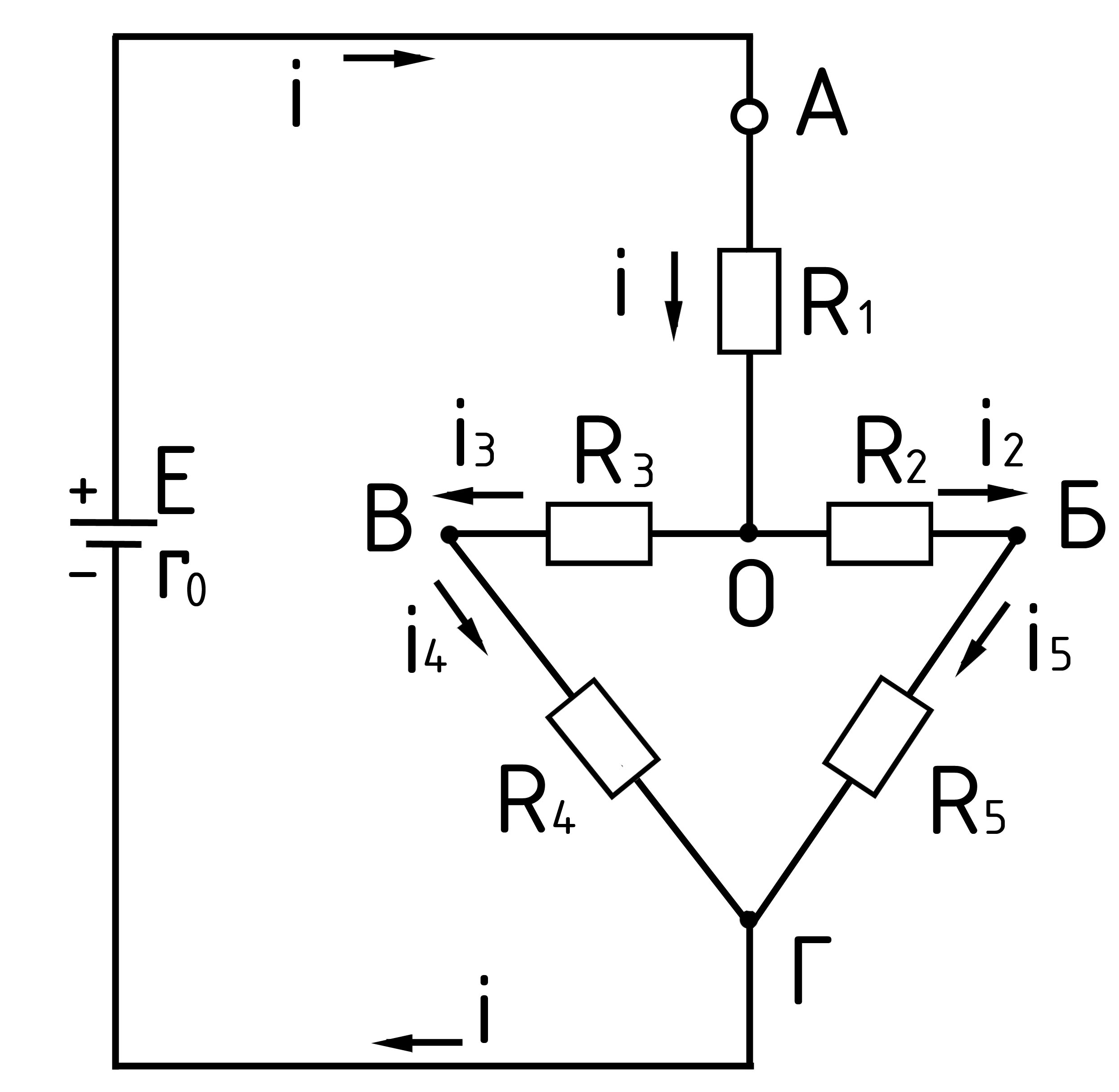
Дано: (рис. 28) Е=3,6 В; r0 = 0,12 Ом; r1 = 8 Ом; r2 = 10 Ом; r3 = 2 Ом; r4 = 4 Ом; r5 = 5 Ом.
Найти: все токи.
Решение задачи:
1. Особенности рассматриваемой цепи.
Покажем на схеме направление общего тока I, который разветвляется в узловой точке А на два: I1 и I2. Дальше следовало бы показать направление тока I3 между узлами Б и В, но он может иметь два направления (показаны на рисунке сплошной и пунктирными стрелками). Действительное направление тока I3 зависит от параметров схемы и определяется только после расчета цепи.
Итак, в рассматриваемой цепи не только величины токов, но их направления (в отдельных ветвях) определяются расчетом.
Кроме того, до сих пор расчет цепей с одним источником энергии основывался на упрощении схемы с последовательно и параллельно соединенными сопротивлениями. Возможен ли такой путь решения данной задачи?
Оказывается, нет. Рассматриваемая цепь не имеет параллельно и последовательно соединенных
сопротивлений. Действительно, с одной стороны,
нет сопротивлений, подключенных к одной и той же паре узлов (условие параллельного соединения), с другой – нет сопротивлений, обтекаемых одним и тем же током (условие последовательного соединения).
Итак, рассматриваемая цепь не может быть разбита на последовательно и параллельно
соединенные участки (ветки). Такие электрические цепи иногда называют сложными, поэтому и рассматриваемую цепь (рис. 28) можно отнести к числу сложных.
| I |
| Б |
| E |
| I |
| I |
| I |
| I |
| I |
| I |
| R |
| R |
| R |
| R |
| R |
| В |
| А |
| Г |
Рис. 28.
2. Вычисление общего сопротивления.
Определить общее сопротивление цепи теми же методами, что и в предыдущих задачах, в данном случае нельзя. Поэтому возникает вопрос: нельзя ли преобразовать схему так, чтобы применение прежних методов стало возможным?
| E |
| r0 |
| I |
| I |
| В |
| А |
| Б |
| Г |
Оказывается, можно, если соединение сопротивлений треугольником преобразовать в соединение звездой или, наоборот, звезду сопротивлений в треугольник. Выполним преобразование для треугольника сопротивлений R1, R2 и R3 (Рис. 28)
а)
б)
Рис. 29 а, б.
Прежде всего перечертим схему без заменяемого треугольника сопротивлении, но с обозначенными вершинами А, Б, В (рис. 29, а). Затем к этим вершинам присоединим звезду сопротивлений RА,RБ и RВ (рис. 29, б). Учитывая, что каждое сопротивление звезды равно произведению двух примыкающих сопротивлений треугольника, разделённому на сумму трёх его сопротивлений, находим:
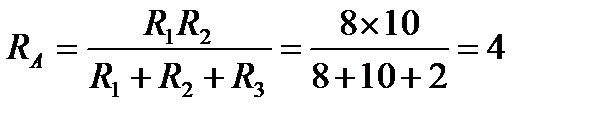 Ом;
Ом;
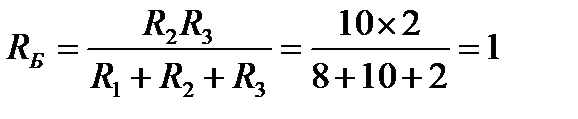 Ом;
Ом;
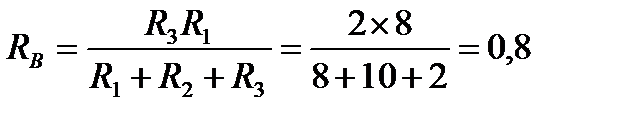 Ом.
Ом.
Дальше расчёт эквивалентной схемы по рис. 29, б ведётся уже известными методами. Действительно, сопротивление RВ соединено последовательно с R4, а сопротивление RБ – последовательно с R5; поэтому для ветви ОВГ общее сопротивление RВ,4=RВ+R4=0,8+4=4,8 Ом, а для ветви ОБГ RБ,5= RВ+R5=1+5=6 Ом. Сопротивление RВ,4 и RВ,5 соединены параллельно, и их общее сопротивление
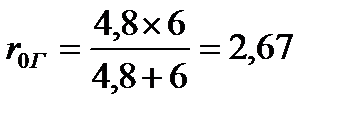 Ом.
Ом.
Общее сопротивление всей цепи Rоб=RА+ r0Г=4+2,67=6,67 Ом.
3. Вычисление токов. Определение токов в цепях, подобных полученной (рис. 29, б), уже выполнялось в предыдущих задачах и приводится здесь без подробных пояснений.
Ток источника
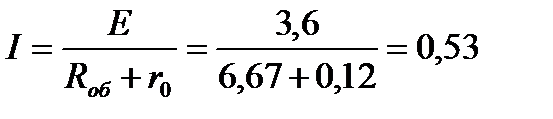 А.
А.
Ток ветви ОВГ
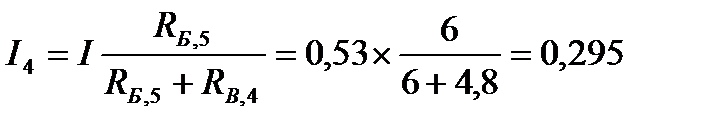
Ток ветви ОБГ
 А.
А.
Поскольку участки ВГ и ГБ (рис. 28 и 29, б) не преобразовались, то вычисление токов I4 и I5 действительны для обеих схем. Переходим к исходной схеме (рис. 28); запишем уравнение по второму закону Кирхгофа для контура ВБГ (ток I3 будем считать направленным, как показано сплошной стрелкой):
 .
.
Подставляя числовые значения, получаем:
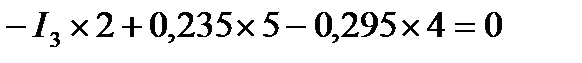
или
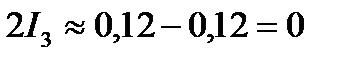 , т.е. I=0;
, т.е. I=0;
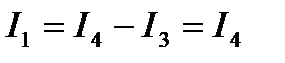 ;
; 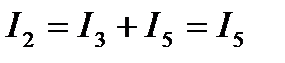 .
.
* Дополнительные вопросы к задаче
1. Случайно ли ток I3 оказался равным нулю?
Рассматривая цепь (рис. 28) называется мостовой. в мостовой цепи ток I3 в ветви ВБ, называемой диагональю моста, равен нулю, если произведения сопротивлений противоположных плеч одинаковы. Действительно, в нашем случае R1R5=8×5=40 и R2R4=10×4=40. Поэтому и оказалось I3=0.
Мостовые схемы широко применяются в технике электрических измерений и, в частности, для измерения сопротивлений.
2. Сколько в рассмотренной цепи (рис. 28) соединений звездой и сколько треугольником?
В этой цепи соединения звездой (R1, R3, R4 и R2, R3, R5) и два соединены треугольником (R1, R2, R3 и R3, R4, R5).
3. Можно ли решить задачу преобразованием звезды в треугольник?
а)
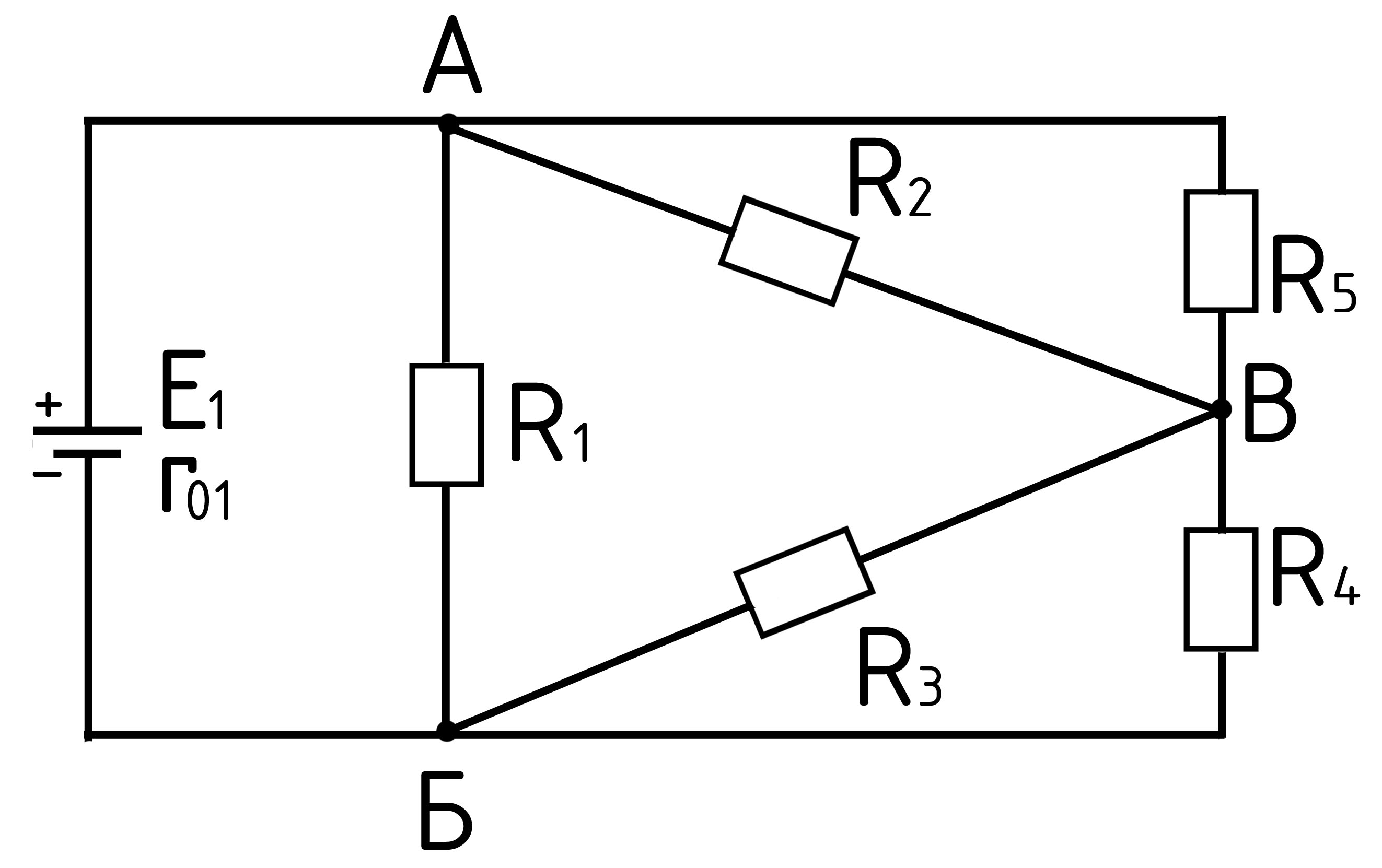
б)
Рис. 30 а,б
Для преобразования можно выбрать любую звезду или любой треугольник. Отдают предпочтение такому преобразованию, которое быстрее приводит к решению задачи. В данном случае можно также успешно решить задачу заменой любой звезды треугольником, например звезды R1,R3,R4.
Прежде всего исключим заменяемую звезду (рис. 30, а) и к вершинам А, Б, и Г присоединим треугольник сопротивлений RАБ, RБГ, RГА (рис. 30, б). Для определения сопротивления треугольника нужно взять сумму трех слагаемых: двух примыкающих сопротивлений звезды и их произведения, разделенного на третье сопротивление звезды.
Таким образом,
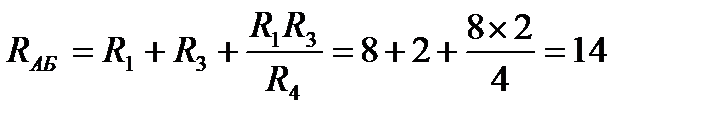 Ом;
Ом;
 Ом;
Ом;
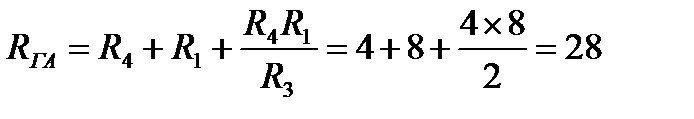 Ом.
Ом.
Далее определим опять общее сопротивление цепи. В полученной схеме (рис. 30, б) имеются две пары параллельного соединенных сопротивлений RАБ и R2; RБГ и R5. Их общие сопротивления равны:
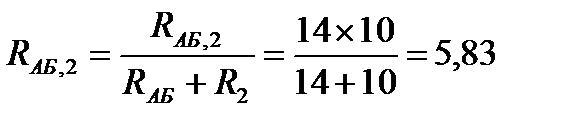 Ом;
Ом;
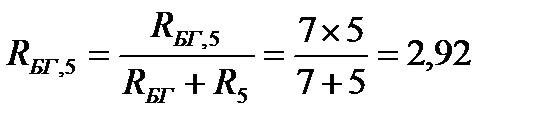 Ом;
Ом;
и общее сопротивление всей цепи
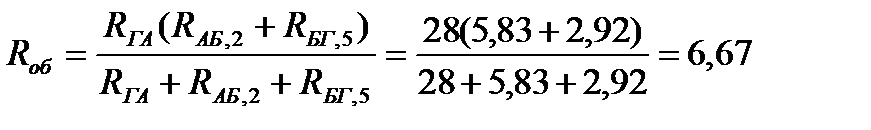 Ом.
Ом.
Как и следовало ожидать, получился тот же результат что и в предыдущем варианте преобразования.
4. Как учесть направление тока в диагонали моста?
В начале решения было указано, что ток I3 может иметь два направления, причём действительное направление заранее неизвестно. Поэтому сначала направление выбираем произвольно. Если направление тока выбрано неправильно, то в результате расчёта получится отрицательное значение тока.
5. Какое наименьшее число узлов и сопротивлений имеет схема, требующая применения метода преобразования соединения сопротивлений треугольником и звездой?
Цепи с двумя и тремя узлами всегда рассчитываются без применения такого преобразования, так как имеют только последовательные и параллельные участки. Но в цепях с четырьмя и более узлами может потребоваться преобразование треугольника сопротивлений в звезду или наоборот.
6. Можно ли при решении этой задачи обойтись без преобразования треугольника в звезду?
Как уже было показано, для упрощения схемы преобразование неизбежно. Но можно обойтись и без преобразования, если воспользоваться методами расчёта сложных цепей.
Date: 2015-07-24; view: 3369; Нарушение авторских прав