
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Раціональний вибір координатних осей і центрів моментів
|
|
1. Вибираємо тіло, рівновагу якого треба розглянути.
2. Звільняємо тіло від в’язей, зображаємо прикладені до тіла активні сили і реакції відкинутих в’язей.
3. Вибираємо систему координат і складаємо рівняння рівноваги.
4. Знаходимо невідомі величини і використовуючи невикористане додаткове рівняння перевіряємо правильність розв’язку.
Доцільно складати рівняння так, щоб в кожному з рівнянь було не більше 2-х (краще одна) невідомих величин. Цього можна досягнути раціональним вибором осей координат і центрів моментів.
За центр моментів доцільно вибирати точку, в якій перетинаються лінії дій 2-х невідомих сил; тоді рівняння моментів буде мати тільки одну невідому величину.
-38-
Напрям координатних осей доцільно вибирати так, щоб вони були перпендикулярні до деяких невідомих сил. При складанні рівнянь проекцій невідомі, перпендикулярні до відповідної осі в це рівняння не увійдуть.
Обчислення доцільно починати з цього рівняння, в яке входить тільки одна невідома величина; найчастіше це рівняння моментів.
9. Балкові системи. Види опор. Опорні реакції
В машинах і спорудах часто зустрічаються так звані балкові системи, або просто балки.
Балкою називають брус з прямолінійною віссю, покладений на опори, який сприймає поперечні навантаження (перпендикулярні до осі). Балка, як правило, має постійний переріз і довжина її набагато більша від розмірів перерізу. Балки застосовуються в будівництві, в машинобудуванні – це вали, осі, а також, елементи корпусів.
Опори балок за їх будовою поділяють на три види.
1. Шарнірно-рухома опора, яка допускає повертання навколо осі шарніра і
лінійне переміщення паралельно опорній площині.
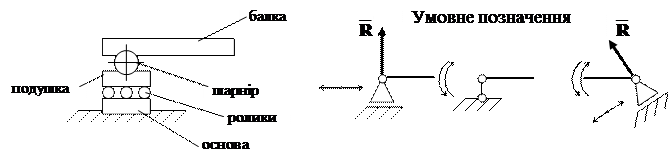
Реакція напрямлена перпендикулярно до опорної поверхні і невідома тільки за величиною.
2. Шарнірно нерухома опора, яка допускає тільки повертання навколо осі шарніра і не допускає лінійних переміщень.
 |
Реакція такої опори напрямлена перпендикулярно до осі шарніра, величина і напрям її невідомі. При розв’язанні задач реакцію розкладають на дві взаємно перпендикулярні складові, невідомі за величиною і відомі за напрямками.
3. Жорстке закріплення (защемлення), яке не допускає ні повороту, ні лінійних
переміщень защемленого кінця.
 -39-
-39-
Реакція защемлення не відома ні за величиною ні за напрямом і її розкладають на складові паралельні осям координат. Крім реакції в защемленні виникає реактивний момент створений парою сил, яка діє в защемленні.
10. Класифікація навантажень
Навантаженнями називають зовнішні сили, які діють на елементи машин і споруд.
За способом прикладання навантаження умовно поділяють на зосереджені та розподілені.
До цих пір розглядались тільки зосереджені сили, вважаючи їх прикладеними в точці. Фактично таких сил не існує; насправді вони до обмеженої площинки, розмірами якої нехтують.
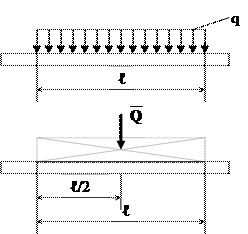 Але в ряді випадків не можна знехтувати тим, що навантаження прикладене неперервно. Неперервні сили можуть бути розподілені по об’єму, по поверхні і по довжині. Навантаження розподілене по довжині характеризується інтенсивністю. Інтенсивність q – це сила, яка припадає на одиницю довжини навантаженої ділянки. Одиниця вимірювання [q] = 1 Н/м.
Але в ряді випадків не можна знехтувати тим, що навантаження прикладене неперервно. Неперервні сили можуть бути розподілені по об’єму, по поверхні і по довжині. Навантаження розподілене по довжині характеризується інтенсивністю. Інтенсивність q – це сила, яка припадає на одиницю довжини навантаженої ділянки. Одиниця вимірювання [q] = 1 Н/м.
При розв’язуванні задач статики розподілене
навантаження заміняють рівнодійною зосередже-
 ною силою Q, чисельно рівною Q = qℓ прикла-
ною силою Q, чисельно рівною Q = qℓ прикла-
деною до середини навантаженої ділянки і на-
прямленою в сторону дії q.
Задача 3.14 (М) Горизонтальна балка підтримує балкон. На балку діє рівномірно
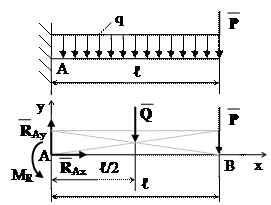 розподілене навантаження інтенсивністю q = 2 кН/м.
розподілене навантаження інтенсивністю q = 2 кН/м.
На балку біля вільного кінця передається навантаження
від колони Р = 2 кН. Відстань від колони до стіни ℓ =
=1,5 м. Визначити реакції в защемленні.
Дано: q = 2 кН/м; Р = 2 кН; ℓ = 1,5 м;
 Знайти: RA, MR -?
Знайти: RA, MR -?
-40-
Розв’язування
Заміняємо розподілене навантаження зосередженою силою:
Q = qℓ = 2 (кН/м)∙ 1,5 м = 3 кН.
Складаємо рівняння рівноваги і розв’язуючи їх, знаходимо невідомі реакції:
Σ Fix = 0; RAx = 0; Σ Fiy = 0; RAy – Q – P = 0;  RAy = P + Q;
RAy = P + Q;
RAy = 2 + 3 = 5 кН; оскільки RAx = 0, то повна реакція RA = RAy = 5 кН і напрям її співпадає з напрямом осі у.
Σ МА = 0; МR - Q∙ ℓ/2 - P∙ℓ = 0;  MR = Q∙ ℓ/2 + P∙ℓ = 3 ∙ 1,5/2 + 2 ∙ 1,5 = 5,25 кНм.
MR = Q∙ ℓ/2 + P∙ℓ = 3 ∙ 1,5/2 + 2 ∙ 1,5 = 5,25 кНм.
Перевірка.
Складаємо додаткове рівняння Σ МВ = МR – RAy∙ℓ + Q∙ℓ/2 = 5,25 - 5∙1,5 + 3∙1,5/2 =
= 0; рівняння рівноваги задовольняється, отже реакції знайдені вірно.
Задача 4.19 (М) Кран для піднімання вантажів складається з балки АВ, нижній
кінець якої з’єднаний з стіною шарніром А, а верхній втриму-
ється горизонтальним тросом ВС. Визначити натяг троса ВС
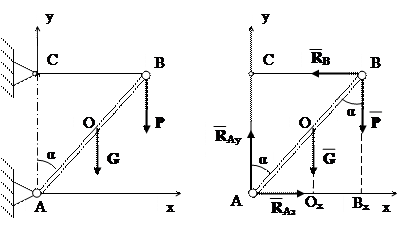 і силу тиску на опору А, якщо відомо, що вага вантажу Р =
і силу тиску на опору А, якщо відомо, що вага вантажу Р =
= 2 кН, вага балки АВ 1 кН і
прикладена до середини балки,
кут α = 450.
Дано:
Р = 2 кН; G = 1 кН;
 α = 450;
α = 450;
Знайти Т, N –?
Розв’язування
За аксіомою 5 (законом рівності дії і протидії) натяг троса за величиною рівний реакції троса – Т = RB, а сила тиску балки на опору А рівна реакції опори (шарніра) – N = RA. Розглядаємо рівновагу балки під дією плоскої системи сил:




 ваги вантажу Р, ваги балки G, прикладеної в т.О посередині балки, реакції троса R B, реакції шарніра А невідомої за напрямом, яку представимо двома складовими вздовж вибраних осей координат – R Ax та R Ay.
ваги вантажу Р, ваги балки G, прикладеної в т.О посередині балки, реакції троса R B, реакції шарніра А невідомої за напрямом, яку представимо двома складовими вздовж вибраних осей координат – R Ax та R Ay.
Складаємо рівняння рівноваги і, розв’язуючи їх, знаходимо невідомі реакції:
Σ Fix =0; RAx – RB = 0; RAx = RB;
Σ Fiy = 0; RAy – P – G = 0;  RAy = P + G = 2 + 1 = 3 кН;
RAy = P + G = 2 + 1 = 3 кН;
Σ МА = 0; RB∙BBx – P∙ABx – G∙AOx = 0; 
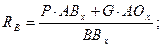
BBx = AC = AB cos α; ABx = AB sin α; AOx = AO sin α = 
RB= 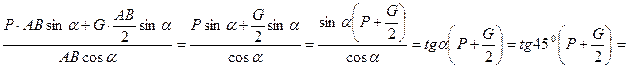
= 1∙(2 + 0,5) = 2,5 кН; RAx = RB = 2,5 кН.
-41-
Перевірка. Складаємо додаткове рівняння рівноваги:
Σ MB = RAx∙BBx - RAy∙ABx + G∙AxOx = RAx∙AB cos α - RAy∙AB sin α +
+ G∙(AB/2) sin α = AB (RAx cos α – RAy sin α + (G/2) sin α) =
= AB∙(2,5∙0,707 - 3∙0,707 + 0,5∙0,707) = 0.
Отже реакції знайдені вірно.
Повна реакція шарніра 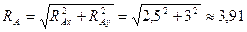 кН.
кН.
Отже, сила натягу троса Т = 2,5 кН; сила тиску в шарнірній опорі N = 3,91 кН.
Домашнє завдання
Задача Визначити реакції опор А і В балки, котра знаходиться під дією
розподіленого навантаження q = 2 кН/м, зосередженої сили F = 6 кН та
пари сил з моментом М = 4 кНм. Довжини ділянок балки та кут між
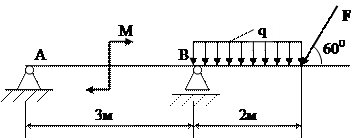 напрямом сили і віссю балки вказані на рис.
напрямом сили і віссю балки вказані на рис.
-42-
11. В’язі з тертям. Сила тертя, коефіцієнт тертя
Абсолютно твердих і гладких тіл в природі не існує. Тому при переміщенні тіла по поверхні іншого тіла завжди виникає опір переміщенню, який називають тертям. Тертя виникая також при намаганні перемістити одне тіло по поверзні іншого. Тертям називають явище опору, яке виникає при переміщенні одного тіла по поверхні іншого, або при намаганні перемістити одне тіло по поверхні іншого.
Тертя – явище дуже поширене в природі і техніці. На терті основана робота пасових і фрикційних передач, гальм, фрикційних муфт. Тертя забезпечує зчеплення з землею коліс автомобілів, тракторів, тобто робить можливою роботу транспортних машин. Тертя між підошвою взуття і грунтом робить можливим ходіння людини. Але в багатьох випадках тертя є шкідливим опором руху, на перемагання якого затрачається значна кількість енергії (тертя в підшипниках валів, між напрямними станини і супортом верстатів) і його намагаються зменшити.
Тертя, яке виникає при намаганні перемістити одне тіло по поверхні іншого у випадку відсутності руху називається тертям спокою.
Тертя, що виникає між двома тілами при переміщенні одного тіла по поверхні другого, називається тертям руху.
В залежності від характеру відносного руху тіл тертя поділяють на тертя ковзання (відносні швидкості тіл різні) і тертя кочення (відносні швидкості точок дотику тіл однакові).
Тертя ковзання як і тертя спокою зумовлене шорсткістю і деформацією поверхонь, а також молекулярним зчепленням притиснутих одне до одного тіл. Тертя ковзання приводить до спрацювання, тобто відшарування матеріалу.
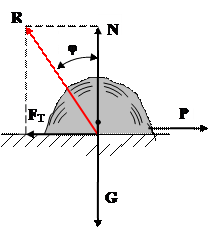 Розглянемо тіло, що знаходиться на горизонтальній площині. Сила тяжіння G зрівноважується нормальною реакцією N. Прикладемо силу Р паралельно до площини. Прикладену силу Р поступово збільшуватимемо – до певного значення Р тіло знаходитиметься в спокої, при дальшому збільшенні Р, тіло почне рухатись, оскільки сила тертя F Т не може зрівноважити зсуваючи силу Р. Найбільше значення сили тертя спокою в момент початку руху тіла називається максимальною силою тертя спокою, або просто силою тертя спокою.
Розглянемо тіло, що знаходиться на горизонтальній площині. Сила тяжіння G зрівноважується нормальною реакцією N. Прикладемо силу Р паралельно до площини. Прикладену силу Р поступово збільшуватимемо – до певного значення Р тіло знаходитиметься в спокої, при дальшому збільшенні Р, тіло почне рухатись, оскільки сила тертя F Т не може зрівноважити зсуваючи силу Р. Найбільше значення сили тертя спокою в момент початку руху тіла називається максимальною силою тертя спокою, або просто силою тертя спокою.
У XVIII ст. французькі вчені Амонтон і Кулон досліджували явище тертя і сформулювали декілька основних законів тертя:
1. Сила тертя не залежить від площі тертьових поверхонь.
2. Сила тертя знаходиться в площині дотичній до поверхонь, що дотикаються, і напрямлена в сторону, протилежну до відносного руху тіла.
3. Сила тертя залежить від матеріалу тіл, шорсткості поверхонь, наявності і виду мащення.
4. Сила тертя спокою прямо пропорційна силі нормального тиску (нормальній реакції).
-43-
Відношення сили тертя до сили нормального тиску називається коефіцієнтом тертя ковзання:
 або FT = f N; f – безрозмірна величина.
або FT = f N; f – безрозмірна величина.
Залежно від того, чи є між тертьовими поверхнями шар мастила, тертя поділяють на три види: сухе тертя (без мастила), граничне (напіврідинне) тертя, рідинне тертя; в останньому випадку тертьові поверхні повністю розділені шаром мастила.
Значення коефіцієнтів тертя для деяких матеріалів:
сталь по сталі (чавуну) – 0,2
бронза по чавуну – 0,15
дерево по дереву – 0,4 – 0,6
сталь по льоду – 0,02
дерево по льоду – 0,035
гума по твердому грунті – 0,5 – 0,6
12. Кут і конус тертя. Умова самогальмування
|
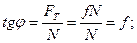 отже – коефіцієнт тертя рівний тангенсу кута тертя.
отже – коефіцієнт тертя рівний тангенсу кута тертя. 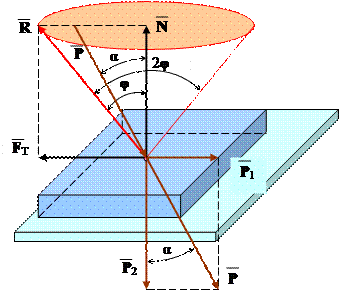 Якщо навколо осі, перпендикулярної до площини дотику тіл обертанням вектора повної реакції утворити поверхню конуса, то такий конус називається конусом тертя. Якщо коефіцієнт тертя у всіх напрямках однаковий, то конус буде круговий. Кут при вершині конуса рівний 2φ. Отже, конус тертя визначає будь-який з можливих напрямків повної реакції R. Нехай на тіло діє сила Р, що утворює з нормаллю до площини дотику кут α., яка намагається зсунути тіло по площині. Розкладемо силу Р на складові Р 2 – силу нормального тиску і зсуваючу силу Р 1: Р1 = Р2 tg α, де Р2 = N.
Якщо навколо осі, перпендикулярної до площини дотику тіл обертанням вектора повної реакції утворити поверхню конуса, то такий конус називається конусом тертя. Якщо коефіцієнт тертя у всіх напрямках однаковий, то конус буде круговий. Кут при вершині конуса рівний 2φ. Отже, конус тертя визначає будь-який з можливих напрямків повної реакції R. Нехай на тіло діє сила Р, що утворює з нормаллю до площини дотику кут α., яка намагається зсунути тіло по площині. Розкладемо силу Р на складові Р 2 – силу нормального тиску і зсуваючу силу Р 1: Р1 = Р2 tg α, де Р2 = N.
За законом тертя FT = f N = f P2 = tg φ P2 – максимальна сила тертя спокою.
При α < φ tg α < tg φ; тоді P1 < FT. Отже, максимальна сила тертя спокою завжди більша від зсуваючої сили. Якщо кут, утворений рівнодійною зовнішніх сил, що діють на тіло, менший від кута тертя, або, інакше кажучи, рівнодійна зовнішніх сил
-44-
проходить всередині конуса тертя, то, якою б не була великою ця рівнодійна, вона не може вивести тіло з стану спокою – це є умова самогальмування.
Задача Визначити при яких значеннях кута нахилу похилої площини, тіло не зісковзуватиме з неї під дією власної ваги.
Розв’язування.
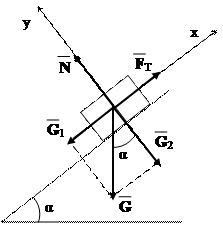 Розглянемо тіло на похилій площині на яке діє сила тяжіння G, яку розкладемо на нормальну складову G 2 і складову вздовж похилої площини G 1: G2 = G cos α; G1 = G sin α.
Розглянемо тіло на похилій площині на яке діє сила тяжіння G, яку розкладемо на нормальну складову G 2 і складову вздовж похилої площини G 1: G2 = G cos α; G1 = G sin α.
Рівняння рівноваги тіла:
Σ Fix = FT – G1 = 0; FT = G1 = G sin α;
Σ Fiy = N – G2 = 0; N = G cos α;
|


tgα = f; але f = tg φ і - якщо кут нахилу похилої площини рівний куту тертя,
то тіло, що лежить на похилій площині, буде під дією власної ваги або рівномірно ковзати вниз, або знаходитись в стані спокою.
Для того, щоб тіло гарантовано не ковзало вниз під дією сили тяжіння необхідно щоб G1 < FT = f N – зсуваючи сила була меншою за максимальну силу тертя спокою.
Тоді G sin α < f G cos α і tg α < f або α < φ – кут нахилу площини має бути менший від кута тертя.
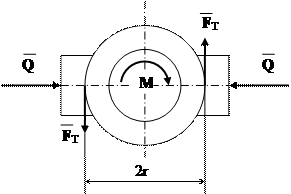 Задача 5.21 (М) До вала прикладена пара сил з моментом М = 100 Нм. На валу знаходиться гальмівне колесо радіусом 25 см. Знайти з якою силою Q треба притискати до колеса гальмівні колодки, щоб колесо залишалось в спокої, якщо коефіцієнт тертя спокою між колесом і колодками f = 0,25.
Задача 5.21 (М) До вала прикладена пара сил з моментом М = 100 Нм. На валу знаходиться гальмівне колесо радіусом 25 см. Знайти з якою силою Q треба притискати до колеса гальмівні колодки, щоб колесо залишалось в спокої, якщо коефіцієнт тертя спокою між колесом і колодками f = 0,25.
Дано: М = 100 Нм;
r = 25 см = 0,25 м;
f = 0,25;
 Знайти Q
Знайти Q
Розв’язування
Умова рівноваги вала:
Σ Мі = 0; - М + МГ = 0;
де МГ - гальмівний момент;
МГ = FT ∙ 2r; FT = f Q;
Звідки 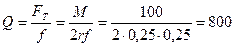 Н.
Н.
-45-
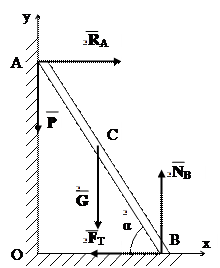
Задача 5.28 (М) Драбина АВ вагою G впирається в гладку стіну і на горизонтальну шорстку підлогу. Коефіцієнт тертя драбини об підлогу рівний f. Під яким кутом α до підлоги треба поставити драбину, щоб по ній могла піднятися людина вагою Р.
Дано: Р і Q.
 Знайти α
Знайти α
Розв’язування.
На драбину діють сили: вага драбини G, прикладена до її середини – т.С, вага людини Р в т.А, нормальна реакція стіни R A, нормальна реакція N B і сила тертя F T. Під дією цих сил драбина знаходиться в рівновазі. Складаємо рівняння рівноваги:
Σ Fix = RA – FT = 0; FT = RA;
Σ Fiy = – P – G + NB = 0; NB = P + G;
Σ MB = – RA ∙ OA + P ∙ OB + G ∙ (OB/2) = 0;
OA = AB sin α; OB = AB cos α; тоді
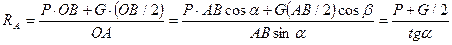 ;
;
RA = FT = f NB = f ∙ (P + G); тоді 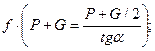

 tg α =
tg α = 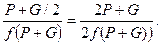
Для того щоб драбина гарантовано не зсунулась, треба щоб
α > 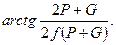
Домашнє завдання
Задача. Визначити величину сили, паралельної похилій площині при рівномірному переміщенні тіла вгору по шорсткій похилій площині, якщо вага тіла G = 10 H, кут нахилу похилої площини α = 450, коефіцієнт тертя f = 0,1.
-46-
Date: 2015-07-24; view: 1885; Нарушение авторских прав