Якщо їх моменти рівні

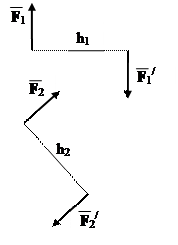
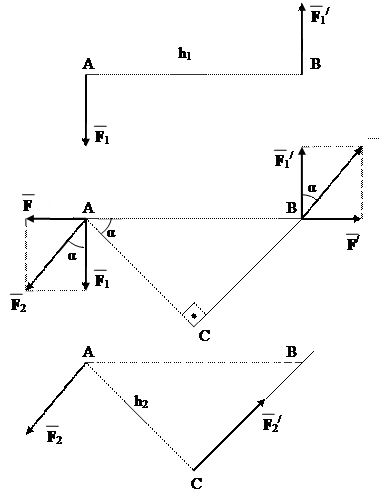Задано пару (F ₁, F ^/₁ ) з плечем h_1.

Її момент М₁ = F₁ h₁.

Приєднаємо зрівноважену систему

двох сил F = – F ^/, що діють вздовж

плеча h₁ = AB.

Додамо попарно сили F і F ₁ та

F ₂ = F + F ₁;

F ₂^/ = F ^/ + F ₁^/.

Так як було приєднано зрівноваже-

ну систему сил F і F ^/, то механіч-

ний стан тіла не змінився.

Отже, пара сил (F ₂, F ₂^/) спричиняє

таку ж саму дію на тіло, як і пара

(F ₁, F ₁^/ ). Тому ці пари еквівалентні:

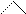
(F ₂, F ₂^/ ) ≡ (F ₁, F ₁^/ ).

З рис. видно, що ВАС = (F ₁, F ₂) =

= α.

Тоді h₂ = h₁ cos α; F₁ = F₂ cos α;

звідки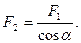

М₁ = F₁ h₁; M₂ = F₂ h₂;

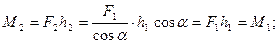
отже, М₂ = М₁.

Наслідки.

Наслідок 1. Не змінюючи механічного стану

тіла, пару сил можна довільно переносити в площині

її дії.

Так як h₂ = h₁ і F₂ = F₁, F₂^/ = F₁^/, то

М₂ = F₂ h₂ = F₁ h₁ = M_1.

Наслідок 2. Механічний стан тіла не зміниться,

я кщо поміняти сили і плече пари так, щоб її момент не

з мінився.

М₁ = М₂; F₁ h₁ = F₂ h₂;

-29-

– щоб момент пари сил не змінився, сили пари повинні бути змінені обернено пропорційно зміні плеча пари.

Наслідок 3. Щоб задати пару сил, достатньо задати її момент, тому термін

«пара сил можна замінити терміном «момент пари» і умовно

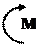
пару сил можна зображати так: або

6. Додавання пар. Умова рівноваги плоскої системи пар сил

Нехай задано три довільні пари, що діють в одній площині.

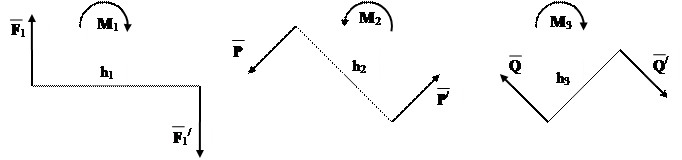
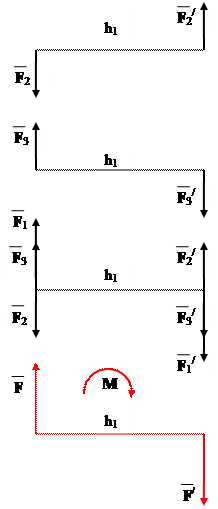
Їх моменти:

М₁ = - F₁ h₁; M₂ = P h₂; M₃ = - Q h₃.

На основі наслідків з теореми про еквівалентні

пари заміняємо другу і третю пари еквівалентними:

(F ₂, F ₂^/) ≡ (P, P ^/); (F ₃, F ₃^/) ≡ (Q, Q ^/ ).

Моменти замінених пар рівні моментам еквівалент-

пар: М₂ = Р₂ h₂ = F₂ h₁; M₃ = Q h₃ = F₃ h₃.

Модуль рівнодійної сил, напрямлених по одній

прямій рівний алгебраїчній сумі сил і ця рівнодійна

напрямлена по цій же прямій:

F = F₁ – F₂ + F₃;

аналогічно F^/ = F₁^/ – F₂^/ + F₃^/. Оскільки за модулем

F^/ = F, то одержано пару сил (F, F ^/)

еквівалентну 3-м заданим парам. Її момент

M_Σ = - F h₁ = - (F₁ – F₂ + F₃) ∙ h₁ = - F₁ h₁ + F₂ h₂ – F₃ h₃ =

= M₁ + M₂ + M₃.

M_Σ = M₁ + M₂…+ M_n або.

Момент рівнодійної пари, еквівалентної заданій

системі пар, що діють в одній площині, рівний

алгебраїчній сумі моментів пар системи.

-30-

Якщо М_Σ = Σ М_і = 0, то діючі на тіло пари утворюють зрівноважену систему.

Отже, необхідна і достатня умова рівноваги системи пар сил, що діють в одній площині

– для рівноваги системи пар сил, діючих на тіло в одній

площині необхідно і достатньо, щоб алгебраїчна сума

їх моментів дорівнювала нулю.

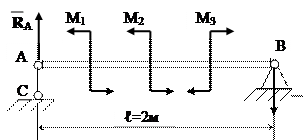
Брус лівим кінцем зв’язаний шарнірно

з стержнем АС, а правим з циліндри-

чним шарніром. На брус діють пари

сил з моментами М₁ = 24 Нм;

М₂ = 36 Нм; М₃ = – 50 Нм.

Визначити реакції, що діють на брус

в т. А і В.

Розв’язування

На брус діє система пар сил. Зрівноважити її можна тільки парою. Отже, в т.А і В повинні діяти реакції, що утворюють пару сил. В т.А на брус діє стержень, реакція R _A якого діє вздовж стержня перпендикулярно до осі бруса, отже, реакція R _B в шарнірі повинна бути перпендикулярна до бруса, напрямлена протилежно до реакції R _A і рівна їй по модулю:

R _B = – R _A; R_B = R_A;

момент пари, яку утворюють реакції M (R _A, R _B) = - R_A ℓ;

позначимо M (R _A, R _B) = M₀ – момент в опорах.

Рівняння рівноваги пар сил Σ М_і = 0; М₀ + М₁ + М₂ + М₃ = 0; підставляючи вираз для М₀, одержимо: - R_A ℓ + M₁ + M₂ + M₃ = 0.

Розв’язуючи останнє рівняння відносно R_A одержимо:

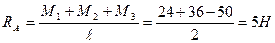; R_B = R_A = 5H.

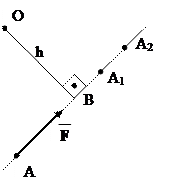7. Момент сили відносно точки

Моментом сили відносно точки називають добуток

модуля сили на найкоротшу відстань від точки до

лінії дії сили: М₀ (F) = ± F h.

Точка О, відносно якої береться момент сили назива -

ється центром моменту; h = ОВ – найкоротша відстань

від центра моменту до лінії дії сили називається пле-

чем сили відносно даного центра.

-31-

Правило знаків аналогічне правилу знаків пар сил: якщо сила F повертаєсвоє плече проти стрілки годинника, то її момент вважають додатнім, і навпаки.

Якщо центр моменту (т.О) лежить на лінії дії сили (h = 0), то момент цієї сили рівний нулю.

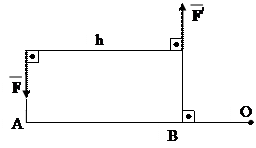Як відомо, сила ковзаючий вектор, тому перенесення сили вздовж лінії дії з т.А в будь-яку іншу точку А₁, А₂ не змінить її плеча, а значить не змінить і моменту сили відносно точки.

Між моментом пари і моментами сил пари

відносно будь-якої точки існує залежність:

алгебраїчна сума моментів сил пари відносно

будь-якої точки є величина стала для заданої

пари і рівна її моменту.

Хай задано пару (F, F ^/ ) з моментом M = F h.

Візьмемо довільну т.О на площині і проведем

перпендикуляри ОВ і ОА до лінії дії сил F і F ^/. Моменти сил відносно т.О:

M_O (F) = F∙ OA; M_O (F ^/) = – F^/ ∙ OB.

Додавши ці моменти, одержимо:

M_O (F) + M_O(F ^/) = F∙OA – F^/∙OB = F∙(OA – OB) = F∙h,

так як F^/ = F і ОА – ОВ = h – плече пари.

Отже, M_O (F) + M_O(F ^/ ) = M.

З розглянутого можна зробити висновок, що між моментом пари сил і моментом сили є суттєва різниця – значення і напрям моменту пари у будь-якій точці є однаковими, а значення і напрям моменту сили відносно точки залежать від положення точки, відносно якої визначається момент.

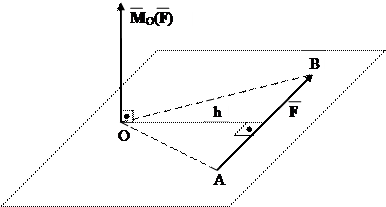
Момент сили відносно точки, так

само як і момент пари сил, можна

розглядати як векторну величину.

Вектор моменту сили F відносно

т.О прикладений в цій же точці О,

напрямлений перпендикулярно до

площини, що проходить через т.О

і лінію дії сили так, щоб при погляді

з кінця вектора, сила повертала своє

плече проти стрілки годинника і

рівний добутку модуля сили на плече.

-32-

Плоска система довільно розташованих сил (ПСЗС)

1. Приведення сили до заданого центру

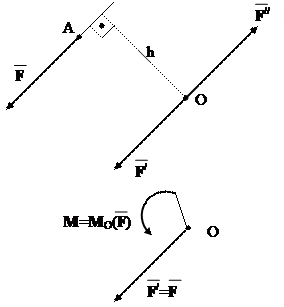Дано: сила F, прикладена в т.А твердого

тіла. Необхідно її перенести в т.О.

Прикладемо в т.О зрівноважену систему

2-х сил F ^// = – F ^/, F ║ F ^/║ F ^//; F = F^/ = F^//.

Одержимо систему

(F, F ^/, F ^// ) ≡ F.

Момент М (F, F ^//) = F h = M_O (F).

Висновок: Силу можна переносити паралельно

з одної точки тіла в іншу, не змінюючи механіч-

ного стану тіла, приєднавши при цьому пару сил,

момент якої рівний моменту сили відносно нової

точки прикладання.

Точка, в яку переноситься сила, називається

центром приведення сили, а перенесення сили у

вибрану точку – приведенням сили до заданого

центру.

2. Приведення ПСДРС до заданого центру. Головний вектор

Date: 2015-07-24; view: 532; Нарушение авторских прав