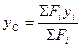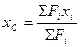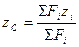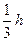Центр ваги

1. Центр паралельних сил

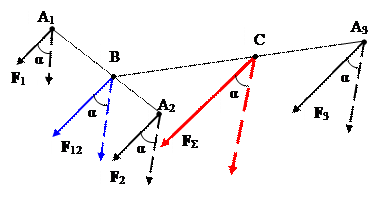
Нехай дано систему 3-х паралельних сил F ₁, F ₂, F ₃, прикладених в точках А₁, А₂, А₃. Як відомо, рівнодійна 2-х паралельних сил рівна по модулю їх сумі, а лінія її дії ділить відрізок прямої, що сполучає точки їх прикладання на частини, обернено пропорційні силам.

Додавши сили F ₁ і F ₂ одержимо їх

рівнодійну F ₁₂ = F ₁ + F ₂ прикладену в т.В, причому

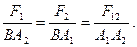
Додавши далі сили F ₁₂ і F ₃, одержимо рівнодійну заданих сил

F _Σ = F ₁₂ + F ₃ = F ₁ + F ₂ + F ₃, прикладену в т.С, яка лежить на відрізку ВА₃, і, яка ділить його на частини

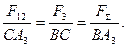
Якщо повернути сили F ₁, F ₂, F ₃ на кут α, не порушуючи їх паралельності, то, повторивши послідовно додавання сил, побачимо, що положення точок В і С не зміниться, так як не зміняться вище записані залежності для їх визначення.

Точку С прикладання рівнодійної F _Σ системи паралельних сил називають центром паралельних сил.

Центром паралельних сил називається точка на лінії дії їх рівнодійної, яка не міняє свого положення відносно точок прикладання даних сил, при повороті сил на один і той же кут із збереженням їх паралельності.

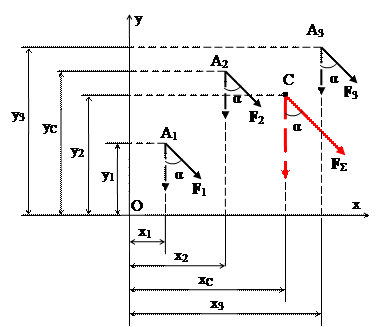Виведемо формули для визначення положення центра будь-якої системи паралельних сил.

Хай задано систему паралельних сил F ₁, F ₂, F ₃, координати точок прикладання цих сил А₁, А₂, А₃ відомі. Позначимо точку прикладання рівнодійної цих сил F _Σ – т.С, її координати позначимо х_С, у_С.

Як відомо F _Σ = F ₁ + F ₂ + F ₃.

Так як положення центра паралельних сил не залежить від їх напряму, повернемо всі задані сили на 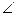α так, щоб вони стали паралельними осі у. Рівнодійна при цьому теж повернеться на той же кут в цю ж

-54-

сторону. Застосуємо теорему Варіньйона про момент рівнодійної відносно т.О:

М_О (F _Σ) = Σ M_O (F _i); F_Σ ∙x_C = F₁∙x₁ + F₂∙x₂ + F₃∙x₃; звідки

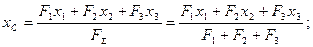
повернувши задані сили на кут 90⁰-α в протилежну сторону, щоб вони стали паралельні до осі х і, використавши теорему про момент рівнодійної, одержимо формулу для другої координати центра тяжіння С:

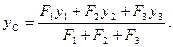
Для будь-якої кількості паралельних сил.

Якщо серед сил є протилежно напрямлені, то сили, співпадаючі з вибраним напрямом, приймають додатними, а протилежні – від’ємними.

.

2. Центр ваги (тяжіння) тіла

Сила, з якою тіло притягається до Землі, називається силою тяжіння. Будь-яке тіло можна розглядати як таке, що складається з великої кількості малих елементарних частинок, на які діють сили тяжіння. Всі ці сили напрямлені до центра Землі по радіусу. Так як розміри тіл дуже малі, порівняно з радіусом Землі (R_З =

= 6380 км), то можна вважати, що прикладені до частинок тіла сили тяжіння паралельні і вертикальні. Отже, сили тяжіння окремих частинок тіла утворюють систему паралельних сил.

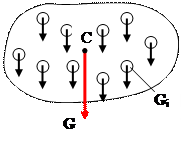Центром тяжіння тіла називається центр паралельних сил тяжіння всіх елементарних частин тіла.

Позначивши G_i – сила тяжіння елементарної частинки тіла і використавши формули для центра паралельних сил, одержимо формули для визначення координат центра тяжіння тіла:

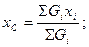
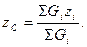
У випадку однорідного тіла G_i = γV_i, де γ – питома вага речовини тіла;

тоді аналогічно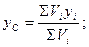

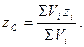
У випадку, коли тіло являє собою однорідну пластину товщиною h, то силу тяжіння її елементарної частинки можна виразити через площу G_i = γhA_i, тоді 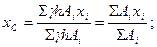аналогічно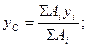

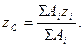
-55-

У випадку, якщо тіло являє собою тонкий стержень постійного поперечного перерізу, то силу тяжіння елементарної частини стержня можна виразити через її довжину ℓ_і: G_i = γAℓi, тоді

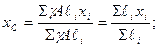аналогічно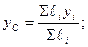

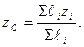
3. Центр тяжіння симетричних тіл

Якщо однорідне тіло має площину симетрії, то центр тяжіння тіла лежить в цій площині.

Аналогічно, якщо однорідне тіло має вісь симетрії, то центр тяжіння тіла лежить на цій осі.

Якщо однорідне тіло має дві осі симетрії, то центр тяжіння знаходиться в точці їх перетину.

4. Положення центра тяжіння простих геометричних фігур

Прямокутник, паралелограм, ромб, квадрат.

Центр тяжіння площі цих фігур лежить в точці перетину діагоналей.

Трикутник.

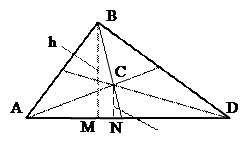Центр тяжіння площі трикутника лежить на відстані рівній третині висоти від кожної з основ

(в точці перетину медіан).

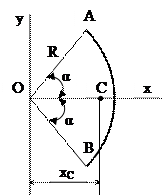Дуга кола радіусом R з центральним кутом 2α.

Систему координат виберемо так, щоб початок координат був в центрі кола, а вісь х ділила дугу наполовину. Тоді

у_С = 0; х_С = 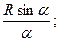α в рад.

При α = 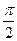(півколо) х_С =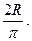

-56-

Круговий сектор

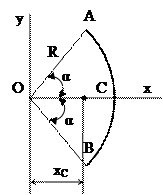у_С = 0; х_С = 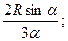α в рад.

При α = 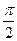(півколо) х_С =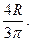

Date: 2015-07-24; view: 718; Нарушение авторских прав