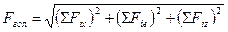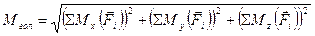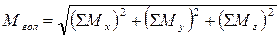Головний вектор і головний момент просторової системи сил

При вивченні теми ПСДРС було показано, що будь-яка плоска система сил приводиться до сили – головного вектора і пари сил, момент якої називають головним моментом, які діють в тій же площині, що і задана ПСДРС.

Міркуючи аналогічно, можна привести до точки сили просторової системи. Але в цьому випадку ми одержимо просторову систему збіжних сил в цій точці і просторову систему пар сил, тобто систему пар, розташованих в різних площинах.

Сили, приведені до однієї точки, можна додати за правилом силового багатокутника (цей багатокутник буде просторовий) і замінити однією еквівалентною силою прикладеною в цій же точці.

Як і для ПСДРС вектор рівний геометричній сумі заданих сил просторової системи називається головним вектором цієї системи:

F _гол = Σ F _i.

Спроектувавши F _гол на осі координат можна одержати:

,

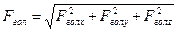де кожна з проекцій рівна 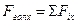; ; 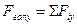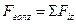. Отже,

....

Одержану при приведенні просторової системи сил до одного центра систему пар, розташованих в різних площинах, теж можна замінити однією еквівалентною парою, момент якої називається головним моментом заданої просторової системи сил відносно вибраного центра приведення. Оскільки пари діють в різних

-51-

площинах, значення головного моменту М_гол не можна одержати алгебраїчним (скалярним) додаванням моментів. Щоб додати моменти пар, діючих в різних площинах, необхідно використати поняття моменту як векторної величини, і додавати моменти як вектори. Якщо розглядати головний момент як вектор, аналогічно як F _гол, то його теж можна розкласти на три складові по осях координат x, y і z величини яких – М_голx, М_голy, М_голz:

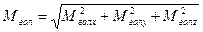, де 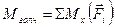; ; 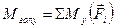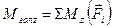– алгебраїчні суми моментів всіх сил системи відносно осей x, y і z..

.

Надалі використовуватимемо скорочений запис:

.

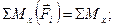
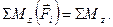
Напрямки головного вектора F _гол і головного моменту М _гол, тобто кути, які вони утворюють з осями координат знаходяться за формулами, аналогічними для визначення напрямку рівнодійної системи збіжних сил.

Для головного вектора: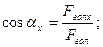

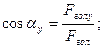
Для головного моменту: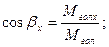

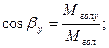
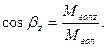
5. Аналітичні умови рівноваги ПрСДРС

У випадку коли F _гол = 0 і М _гол =0 система сил знаходиться в рівновазі. Звідси витікають рівняння рівноваги

– рівняння рівноваги ПрСДРС.

Якщо задано просторову систему паралельних сил, то, вибравши систему координат так, щоб одна з осей була паралельна силам, наприклад, вісь z, одержимо

– – рівняння рівноваги просторової системи

паралельних сил (ПрСПС).

-52-

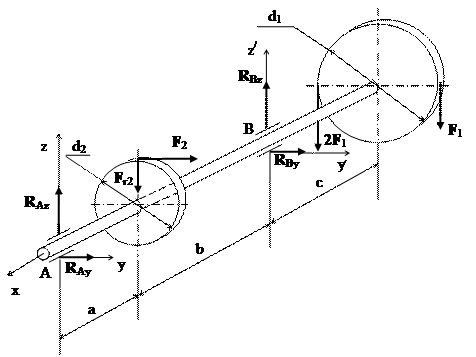
Задача На вал жорстко насаджені шків і зубчасте колесо, навантажені як показано на рис. Визначити сили F₂, F_r2 = 0,4F₂, а також реакції опор, якщо значення сили, прикладеної до шківа F₁ = 200 Н. Діаметр шківа d₁ = 0,5м, діаметр колеса d₂ = = 0,2м, відстані між колесом, шківом і підшипниками (опорами) відповідно рівні

а = 0,2м, b = 0,3м, с = 0,2м.

Дано: F₁ = 200 Н;

F_r2 = 0,4 F₂;

а = c = 0,2 м;

_ b = 0,3 м;___

F₂, F_r2, R_Az, R_Ay,

R_Ax, R_By, R_Bz -?

Розв’язок

Σ М_x = - F₂ ∙ 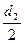- F₁ ∙ 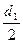+ 2F₁ ∙ 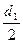= 0;

;

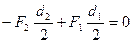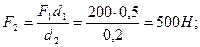
F_r2 = 0,4 F₂ = 0,4∙500 = 200 Н;

Σ M_y = – F_r2∙a – 2F₁∙(a + b + c) – F₁∙(a + b + c) + R_Bz∙(a + b) = 0;

R_Bz =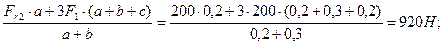

Σ M_z = - F₂∙a – R_By∙(a + b) = 0; R_By =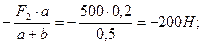

Σ F_ix ≡ 0 (тотожність, оскільки жодна сила не дає проекції на вісь х);

Σ F_iy = 0; R_Ay + F₂ + R_By = 0; R_Ay = – R_By – F₂ = – 500 – (–200) = –300 H;

Σ F_iz = 0; R_Az – F_r2 – F₁ – 2F₁ + R_Bz = 0; R_Az = F_r2 + 3F₁ – R_Bz = 200 +3∙200 – 920 =

= – 120 H.

Знаки «–» для R_By, R_Ay, R_Az означають, що ці реакції напрямлені протилежно до напрямків, вибраних на рис.

Для перевірки складаємо рівняння моментів відносно осей z^/ i y^/:

Σ M_z^/ = R_Ay ∙ (a + b) + F₂ ∙ b = - 300 ∙ (0,2 + 0,3) + 500 ∙ 0,3 = 0;

Σ M_y^/ = – R_Az ∙ (a + b) + F_r2 ∙ b – 2F₁ ∙ c - F₁ ∙ c = –(–120)∙(0,2+0,3) + 200 ∙ 0,3 –

– 3 ∙ 200 ∙0,2 = 0, отже реакції знайдені вірно.

Можна для визначення реакцій R_Ay та R_Az складати рівняння моментів відносно осей y^/ та z^/, а перевірку проводити за рівняннями проекцій сил.

-53-

Date: 2015-07-24; view: 1090; Нарушение авторских прав