
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Парі сил, момент якої рівний головному моменту
|
|
Графічно головний вектор є замикаючою стороною силового багатокутника, побудованого на заданих силах.
Аналітично головний вектор можна визначити методом проекцій:
модуль: Fгол = 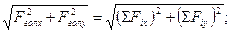
 напрям: cos α = cos ( F гол^, х) =
напрям: cos α = cos ( F гол^, х) = 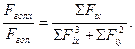
Модуль і напрям головного векторане залежить від вибору центра приведення.
Значення головного моментузалежить від вибору центра приведення (крім випадку коли Fгол = 0), так як із зміною центра приведення змінюються плечі заданих сил.
3. Рівнодійна ПСДРС
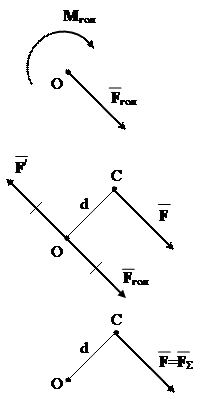
Доведемо, що в загальному випадку ПСДРС можна
привести до однієї рівнодійної сили, тобто знайти таку
точку, відносно якої головний момент системи рівний
нулю (Мгол = 0).
Хай, привівши задану ПСДРС до довільного центра –
 т.О, одержано головний вектор F гол і пара сил з моментом
т.О, одержано головний вектор F гол і пара сил з моментом
Мгол.

 Зобразимо Мгол парою сил (F/, F), які паралельні силі
Зобразимо Мгол парою сил (F/, F), які паралельні силі
 F гол і рівні їй за модулем:
F гол і рівні їй за модулем:




 (F ║ F /║ F гол ), (F = F/ = Fгол); М (F /, F) = Mгол.
(F ║ F /║ F гол ), (F = F/ = Fгол); М (F /, F) = Mгол.

 Одну з сил пари F / прикладемо в т.О протилежно до F гол,
Одну з сил пари F / прикладемо в т.О протилежно до F гол,

 Тоді друга сила F буде напрямлена в той же бік що й F гол,
Тоді друга сила F буде напрямлена в той же бік що й F гол,
 а точку прикладання сили F знайдемо з співвідношення
а точку прикладання сили F знайдемо з співвідношення
 Мгол = F ∙ d; звідси плече сили F
Мгол = F ∙ d; звідси плече сили F


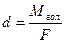 , де F = Fгол.
, де F = Fгол.
Систему сил (F /, F гол) відкинемо як зрівноважену.
-34-
 |  |



 Залишиться тільки одна сила F еквівалентна F гол і М гол, тобто рівнодійна заданій ПСДРС. Позначимо F = F Σ.
Залишиться тільки одна сила F еквівалентна F гол і М гол, тобто рівнодійна заданій ПСДРС. Позначимо F = F Σ.

 Отже, в загальному випадку F гол і F Σ рівні за модулем і однакові за напрямом F Σ = F гол, але не є еквівалентними.
Отже, в загальному випадку F гол і F Σ рівні за модулем і однакові за напрямом F Σ = F гол, але не є еквівалентними.
Модуль рівнодійної FΣ = Fгол = 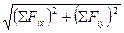 , а положення її лінії дії
, а положення її лінії дії
визначається плечем 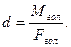
4. Теорема Варіньйона та її застосування





 При визначенні положення лінії дії рівнодійної F Σ ПСДРС було одержано, що Мгол = М (F, F /) = MO (F). Так як F = F Σ рівнодійна, то Мгол = МО (F Σ). Але
При визначенні положення лінії дії рівнодійної F Σ ПСДРС було одержано, що Мгол = М (F, F /) = MO (F). Так як F = F Σ рівнодійна, то Мгол = МО (F Σ). Але
 Мгол = Σ МО (F i).
Мгол = Σ МО (F i).
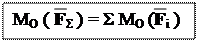 Так як за центр приведення можна взяти будь-яку точку площини дії даної системи, то в загальному випадку одержимо
Так як за центр приведення можна взяти будь-яку точку площини дії даної системи, то в загальному випадку одержимо
 Мгол = Σ МО (F i) і – момент рівнодійної ПСДРС
Мгол = Σ МО (F i) і – момент рівнодійної ПСДРС
відносно будь-якої точки, взятоїв площині дії сил, рівний алгебраїчній сумі моментів сил системи відносно тієї ж точки.
З допомогою теореми Варіньйона розв’язуються багато задач механіки.
а) Визначення рівнодійної плоскої системи паралельних сил
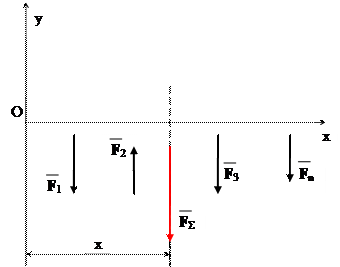 |



 Дано: F 1 ║ F 2 ║ F 3 ║…║ F n.
Дано: F 1 ║ F 2 ║ F 3 ║…║ F n.
Рівнодійна сил





 F Σ = F 1 + F 2 + F 3 +…+ F n = Σ F i;
F Σ = F 1 + F 2 + F 3 +…+ F n = Σ F i;
|
Тоді рівнодійна
FΣ = Fy = Σ Fiy = Σ Fi;
 якщо Σ Fiy > 0, то F Σ напрямлена в бік
якщо Σ Fiy > 0, то F Σ напрямлена в бік
додатного напряму осі у;
 якщо Σ Fiy < 0, то F Σ напрямлена
якщо Σ Fiy < 0, то F Σ напрямлена
протилежно до осі у.

 Згідно теореми Варіньйона
Згідно теореми Варіньйона



 MO (F Σ) = MO (F 1) + MO (F 2) + MO (F 3) +…+ MO (F n) = Σ MO (F i);
MO (F Σ) = MO (F 1) + MO (F 2) + MO (F 3) +…+ MO (F n) = Σ MO (F i);
 але MO (F Σ) = F∙x; отже х =
але MO (F Σ) = F∙x; отже х = 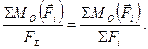

 Якщо х вийде із знаком «–», то це означає, що лінію дії рівнодійної F Σ треба відкладати протилежно до додатного напряму осі х, тобто вліво від т.О.
Якщо х вийде із знаком «–», то це означає, що лінію дії рівнодійної F Σ треба відкладати протилежно до додатного напряму осі х, тобто вліво від т.О.
-35-
б) Визначення моменту сили відносно початку координат

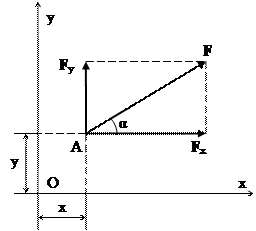
Розкладемо вектор сили F на складові паралельні


 осям координат: F = F x + F y;
осям координат: F = F x + F y;

 по модулю | F x| = Fx; | F y| = Fy.
по модулю | F x| = Fx; | F y| = Fy.
За теоремою Варіньйона



 MO (F) = Σ MO (F i) = MO (F x) + MO (F y) =
MO (F) = Σ MO (F i) = MO (F x) + MO (F y) =
= – Fx y + Fy x = – F cos α ∙ y + F sin α ∙ x =
= F (x sin α – y cos α).
в) Визначення моменту сили відносно опори стержня
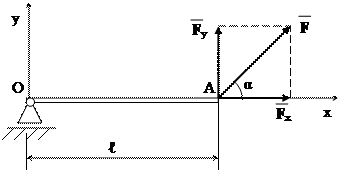
Нехай на стержень діє сила F під
кутом α до стержня.
Розкладемо силу F на дві складові F x,
напрямлену вздовж стержня, та F y,
перпендикулярно до стержня.
За теоремою Варіньйона:


 MO (F) = MO (F x) + MO (F y).
MO (F) = MO (F x) + MO (F y).

 Але MO (F x) = 0 – лінія дії F x прохо-
Але MO (F x) = 0 – лінія дії F x прохо-

 дить через т.О. Тоді MO (F) = MO (F у) = F sin α ∙ ℓ.
дить через т.О. Тоді MO (F) = MO (F у) = F sin α ∙ ℓ.
5. Часткові випадки приведення ПСДРС
 |
Загальний випадок F гол ≠ 0, Мгол ≠ 0 – система приведена до головного вектора і головного моменту.

 Система може бути приведена до однієї рівнодійної, яка дорівнює головному вектору (F Σ = F гол), лінія дії рівнодійної знаходиться відносно заданого центра приведення на відстані
Система може бути приведена до однієї рівнодійної, яка дорівнює головному вектору (F Σ = F гол), лінія дії рівнодійної знаходиться відносно заданого центра приведення на відстані 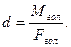
Часткові випадки:
 |
1) F гол ≠ 0; Мгол = 0 – система приведена до рівнодійної, лінія дії якої проходить через центр приведення, і рівнодійна співпадає з головним вектором системи.


 2) F гол = 0; Мгол ≠ 0 – система приведена до пари сил, момент якої рівний головному моменту. Рівнодійна системи сил рівна нулю (F Σ = F гол = 0).
2) F гол = 0; Мгол ≠ 0 – система приведена до пари сил, момент якої рівний головному моменту. Рівнодійна системи сил рівна нулю (F Σ = F гол = 0).
-36-
Оскільки одна і та ж система сил не може бути еквівалентною різним парам з різними моментами, а тільки одній, то величина і знак (напрям) Мгол не залежить від вибору центра приведення.
3) 
 F гол = 0; Мгол = 0 – система сил знаходиться в рівновазі.
F гол = 0; Мгол = 0 – система сил знаходиться в рівновазі.
Домашнє завдання
Задача Визначити величину і положення лінії дії рівнодійної двох паралельних
сил, напрямлених в одну сторону, якщо відстань між ними ℓ = 3 м, модулі сил
F1 = 10 Н, F2 = 20 Н. Порівняти відношення відстаней від сил до рівнодійної і
відношення модулів сил. Застосувати теорему Варіньйона. Для полегшення
розрахунків точку відліку сумістити з лінією дії однієї з сил.
6. Умови та рівняння рівноваги ПСДРС
 |
Умовами рівноваги плоскої системи сил є F гол = 0; Мгол = 0; але F гол = Σ F i, a
Mгол = Σ МО (F i),
|
отже – необхідні умови рівноваги ПСДРС.
|
Але, якщо Σ F i = 0, то і Σ Fix = 0 і Σ Fiу = 0. Звідси
|
|
|
;; – І-а форма рівнянь рівноваги.
Для рівноваги ПСДРС необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил системи на кожну з координатних осей дорівнювала нулю і алгебраїчна сума моментів цих сил відносно будь-якої точки площини дорівнювала нулю.
Так як рівнянь рівноваги три, то для розв’язку задачі необхідно, щоб кількість невідомих було не більше 3-х.
Якщо скласти два рівняння моментів і додати до них одне рівняння проекцій на будь-яку вісь, не перпендикулярну до прямої, що проходить через вибрані центри моментів, то одержимо ІІ-у форму рівнянь рівноваги:
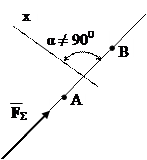 |
|
|
|
;;
|
|
|
або;;;; – ІІ-а
форма рівнянь рівноваги.
Для рівноваги ПСДРС необхідно і достатньо, щоб алгебраїчні
с уми моментів сил відносно будь-яких точок, а також
алгебраїчна сума проекцій сил на вісь, не перпендикулярну
прямій, що проходить через ці точки дорівнювала нулю.
-37-
Третій вид рівнянь рівноваги одержимо, якщо замість рівняння проекцій до 2-х рівнянь суми моментів відносно двох довільних точок А і В додати 3-є рівняння моментів сил відносно будь-якої іншої точки, що не лежить на прямій, яка сполучає точки А і В:
|
|
|
;; – Ш-я форма рівнянь
рівноваги.
Для рівноваги ПСДРС необхідно і достатньо, щоб алгебраїчні суми моментів сил відносно будь-яких 3-х точок площини, що не лежать на одній прямій, дорівнювали нулю.
7. Рівняння рівноваги плоскої системи паралельних сил (ПСПС)
Умови рівноваги ПСПС є частковим випадком умов рівноваги, виведених раніше для ПСДРС.
Якщо розташувати осі координат так, щоб х ┴ F i, а вісь y║ F i, то рівняння Σ Fix ≡ 0 – перетвориться в тотожність і одержимо Σ Fiy = Σ Fi = 0; отже
|
|
; – І-а форма рівнянь рівноваги ПСПС.
Для рівноваги ПСПС необхідно і достатньо, щоб алгебраїчна сума всіх сил дорівнювала нулю, і щоб алгебраїчна сума моментів всіх сил відносно будь-якої точки площини також дорівнювала нулю.
Другий вид рівнянь одержимо, якщо складемо рівняння моментів відносно 2-х точок А і В, що лежать на прямій не паралельній лініям дії сил:
|
|
; – ІІ-а форма рівнянь рівноваги ПСПС.
Для рівноваги ПСПС необхідно і достатньо, щоб алгебраїчна сума моментів всіх сил відносно 2-х будь-яких точок площини,що лежать на прямій не паралельній лініям дії сил дорівнювала нулю.
8. Порядок розв’язування задач на рівновагу плоскої системи сил
Date: 2015-07-24; view: 743; Нарушение авторских прав