Просторова система сил

1. Просторова система збіжних сил (ПрСЗС). Паралелепіпед сил.

Система сил, лінії дії яких лежать в різних площинах називається просторовою. Просторова система сил називається збіжною, якщо лінії дії всіх сил перетинаються в одній точці.

Якщо до прикладених в т.А сил F ₁ і F ₂ приєднати силу F ₃, яка не лежить в площині П дії 2-х перших сил, то одержимо найпростішу просторову систему збіжних сил. Визначимо рівнодійну цих сил.

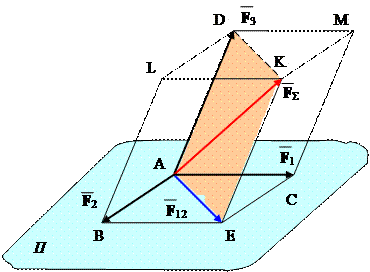Побудувавши паралелограм ABEC на силах F ₁ і F ₂ знайдемо їх рівнодійну F ₁₂ = F ₁ + F ₂;

Побудувавши паралелограм AEKD на силах F ₁₂ і F ₃ знайдемо рівнодійну цих сил

F _Σ = F ₁₂ + F ₃ = F ₁ + F ₂ + F ₃.

Отже рівнодійна F _Σ є векторною сумою сил F ₁, F ₂, F ₃.

Як видно паралелограм ABEC є гранню, а паралелограм AEKD діагональним перерізом паралелепіпеда в якому задані сили є ребрами одного з його тригранних кутів. Отже, рівнодійна просторової

системи трьох сил, прикладених в одній точці, прикладена в цій же точці і рівна за модулем і напрямком діагоналі паралелепіпеда, побудованого на цих силах.

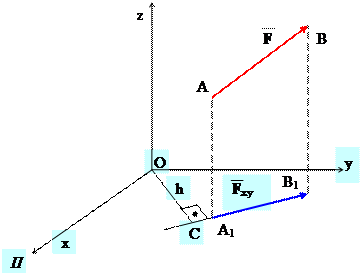
2. Проекція сили на осі координат.

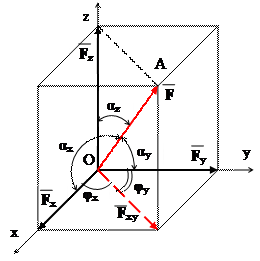Використовуючи правило паралелепіпеда можна розв’язати обернену задачу – розкласти силу на три складовы за заданими напрямками. Часто э доцыльним розкласти силу на складові, напрямлені вздовж трьох осей просторової системи координат.

Нехай задано силу F. Виберемо систему координат так, щоб її початок співпадав з початком вектора сили F. З кінця F опустимо перпендикуляр на пл. ху і вісь z і розкладемо силу F на складові F _xy та F _z, а складову F _xy на складові F _x і F _y. Отже, F = F _x + F _y + F _z. Як видно з рис., складові F _x, F _y, F _z є ребрами прямокутного паралелепіпеда, діагональ якого є заданою силою F.

-47-

Числові значення складових рівні проекціям сили на осі. Ці проекції позначимо F_x, F_y, F_z. Знаючи проекції сили на осі координат, можна знайти модуль і напрям вектора сили:

модуль сили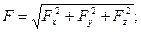

напрямляючі косинуси cos α_x = cos (F,^x) = 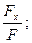cosα_y = cos (F,^y) =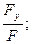

cos α_z = cos (F,^z) =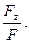

Положення вектора F можна задати також кутом α_z = (F,^z) і одним із кутів φ_х або φ_y, утворених пл. AOz з однією з координатних площин xOz або yOz. Тоді

F_x = F_xy cos φ_x = F sin α_z cos φ_x;

F_y = F_xy sin φ_x = F sin α_z sin φ_x;

F_z = F cos α_z.

3. Рівнодійна ПрСЗС. Аналітичні умови рівноваги ПрСЗС.

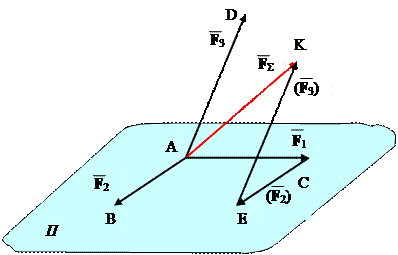Для того, щоб знайти рівнодійну трьох сил, прикладених в одній точці, паралелепіпед будувати не обов’язково; можна обмежитись побудовою просторового силового багатокутника (рис.). З рис. видно, що рівнодійна F _Σ сил F ₁, F ₂, F ₃ відповідає замикаючій стороні багатокутника АСЕК і є їх векторною сумою

F _Σ = F ₁ + F ₂ + F ₃.

Аналогічно, будуючи силовий багатокутник, можна знайти геометричну суму або рівнодійну

Будь-якої кількості збіжних сил, перенісши їх попередньо в точку перетину ліній дії:

F _Σ = F ₁ + F ₂ +…+ F _n або F _Σ = Σ F _і.

Рівнодійна просторової системи збіжних сил рівна за модулем і напрямком замикаючій стороні багатокутника, побудованого на цих силах.

Оскільки силовий багатокутник просторової системи сил не лежить в одній площині, тому геометричний і графічний способи знаходження рівнодійної є неприйнятні. Рівнодійну ПрСЗС можна визначити лише аналітично – методом проекцій. Відмінність від проектування ПСЗС полягає в тому, що тепер сили проектуються на три осі координат.

Додавши алгебраїчно проекції сил на кожну з осей координат, одержимо проекції шуканої рівнодійної

F_Σx = Σ F_ix; F_Σy = ΣF_iy; F_Σz = Σ F_iz, які зображають ребра прямокутного паралелепіпеда, а його діагональ – рівнодійну. Тому модуль рівнодійної

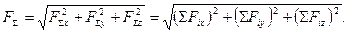
-48-

Напрям рівнодійної можна знайти за напрямляючими косинусами кутів, які вона утворює з осями координат

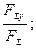cos α_x = cos (F _Σ,^x) = cos α_y = cos (F _Σ,^y) = cos α_z = cos (F _Σ,^_z) =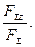

Якщо система ПрСЗС знаходиться в рівновазі, то рівнодійна F _Σ = 0. Але тоді повинні бути рівні нулю кожна з трьох її проекцій: F_Σx = 0; F_Σy = 0; F_Σz = 0.

Отже,;; – це і є аналітичні умови

(рівняння) рівноваги ПрСЗС.

Для рівноваги ПрСЗС необхідно і достатньо, щоб алгебраїчні суми проекцій всіх сил на кожну з трьох координатних осей були рівні нулю.

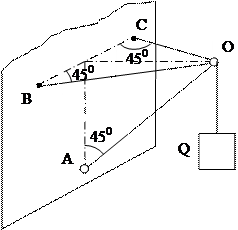
Задача 6.4 (М) Знайти зусилля S₁ і S₂ в стержнях АВ і АС і зусилля в тросі AD,

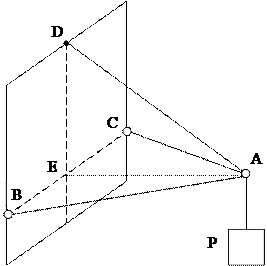якщо дано 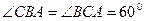, 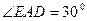. Вага вантажу Р =

= 300 Н. Пл. АВС – горизонтальна. Кріплення стержнів у точках А, В, С – шарнірні.

Розв’язування

Проведемо осі координат, як показано на рис. Прикладемо до вузла А діючу силу Р, зумовлену вагою вантажу, та реакції троса R _D і стержнів R _C і R _B.

Складемо рівняння рівноваги:

Σ F_ix = 0; R_Csin30⁰ – R_Bsin30⁰ = 0; R_B = R_C;

Σ F_iy = 0; R_Bcos30⁰ + R_Ccos30⁰– R_Dcos30⁰ = 0; так як R_C = R_B, то 2R_Bcos30⁰ = R_Dcos30⁰;

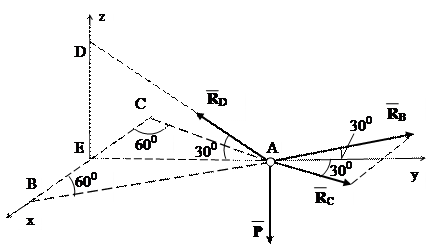
2R_B = R_D;

Σ F_iz = 0; R_Dsin30⁰ – P = 0; (реакції R _B і R _C проекції на вісь z не дають, так як лежать в пл. ху 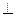z).

R_D =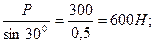

R_B = R_C =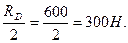

За V-ю аксіомою натяг троса і зусилля в стержнях рівні за модулем і протилежні за напрямом їх реакцій:

T = R_D = 600 H; S₁ = S₂ = R_B = R_C = 300 H.

-49-

Домашнє завдання

Задача 6.3 (М) Вантаж Q = 100 Н підтримується брусом АО, шарнірно закріпленим в т.А і нахиленим під кутом 45⁰ до горизонту, і двома горизонтальними ланцюгами ВО і СО однакової довжини; 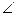СВО = 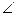ВСО = 45⁰. Знайти зусилля S в брусі і натяг Т ланцюгів.

4. Момент сили відносно осі.

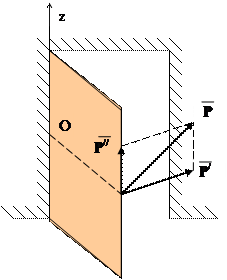Нехай сила Р прикладена до тіла, яке може обертатись навколо осі, наприклад до дверей, що обертаються на петлях навколо осі z. Розкладемо силу Р на дві складові - Р 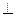^/ z і Р ^// ║ z. Ясно, що складова Р ^// не може надати дверям обертання, ця сила може тільки зсунути двері по осі z. Обертальну дію викликає тільки складова Р ^/, що лежить в площині перпендикулярній до осі z. Отже мірою обертової дії сили Р відносно осі є момент проекції цієї сили на площину перпендикулярну до осі z, відносно точки перетину осі з площиною. Цей момент називають моментом сили Р відносно осі z. Отже, момент сили відносно осі рівний моменту проекції цієї сили на площину, перпендикулярну до осі, відносно точки перетину осі з площиною:

M_Z (F) = M_O (F _xy) = F_xy∙h.

Момент сили вважається додатнім, якщо при погляді з додатного напряму осі, сила викликає обертання проти стрілки годинника і навпаки.

Слід зауважити, що:

момент сили відносно даної осі не змінюється при перенесенні сили вздовж лінії

дії, так як при цьому не змінюється ні проекція, ні її плече;

момент сили відносно осі рівний нулю, тоді, коли лінія дії і вісь лежать в одній

площині. При цьому можуть бути два випадки:

1) сила F паралельна осі (F ║ z). В цьому випадку рівна нулю проекція сили на площину перпендикулярну до осі (F_xy = 0);

2) лінія дії сили перетинає вісь. В цьому випадку проекція сили проходить через точку перетину осі з площиною, і її плече відносно цієї точки рівне нулю (h = 0).

-50-

Для визначення моменту сили відносно осей координат її зручно розкласти на складові, паралельні цим осям.

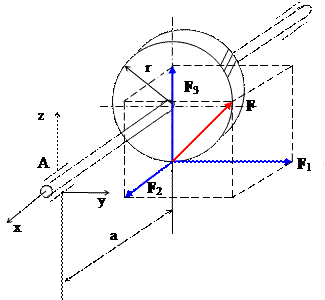На рис. схематично зображено

колесо косозубої передачі. Силу F,

що діє на зуб колеса, можна розкла-

сти на складові F₁, F₂, F₃, які пара-

лельні осям координат, проведеним

через одну з опор вала – т. А:

F ₁ || y, F ₂ || x, F _z || z.

Легко встановити, що:

M_x (F) = M_x (F ₁) = F₁×r;

M_y (F) = M_y (F ₂) + M (F ₃) = -F₂×r + F₃×a;

M_z (F) = M_z (F ₁) = - F₁×a.

4. Просторова система довільно розміщених сил (ПрСДРС).

Date: 2015-07-24; view: 1805; Нарушение авторских прав