Вычеты и их приложения

Вычетом функцииf (z) в особой точкеa называется коэффициент при первой отрицательной степени ряда Лорана функции f (z) в проколотой окрестности точки a:

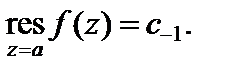(29.41)

Вычет функции f (z) в особой точке a может быть найден по формуле:

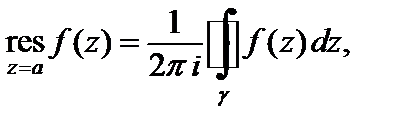(29.42)

где 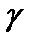– положительно ориентированная окружность 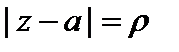такая, что функция f (z) аналитична всюду на круге 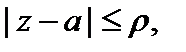за исключением точки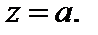

Если a – устранимая особая точка функции f (z), то 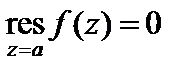и, значит, 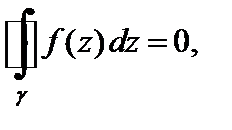где контур 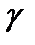положительно ориентированная окружность 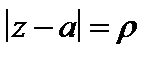такая, что f (z) аналитична всюду на круге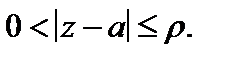

Если a – простой полюс функции f (z), то

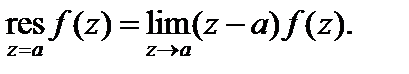(29.43)

Если функцию f (z) можно записать в виде:

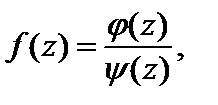
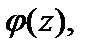
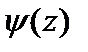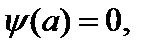
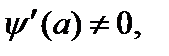
где аналитичны в точке a и 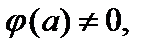т. е. a – простой полюс функции f (z), то

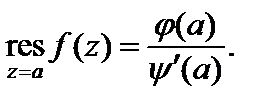(29.44)

Если a – полюс k -го порядка функции f (z), то

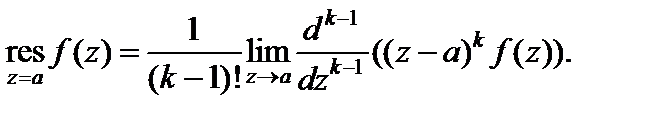(29.45)

Основная теорема о вычетах. Пусть функция f (z) является аналитической во всех точках односвязной области D, кроме конечного числа особых точек, и Г – замкнутая положительно ориентированная кривая, которая лежит в D и ограничивает область, содержащую особые точки 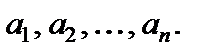Тогда

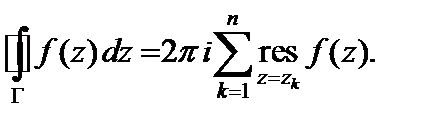(29.46)

Вычетом функции f(z) в точке 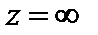( 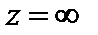– изолированная особая точка функции f (z)) называется число, равное противоположному по знаку коэффициенту при первой отрицательной степени ряда Лорана функции f (z) в окрестности точки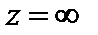

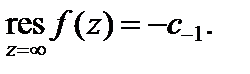(29.47)

Вычет функции f (z) в точке 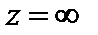может быть найден по формуле:

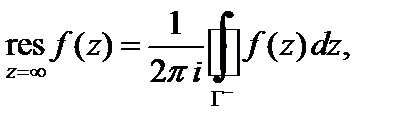(29.48)

где 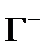– окружность достаточно большого радиуса, проходимая по часовой стрелке.

В устранимой особой точке 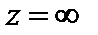вычет может быть и ненулевым (в отличие от конечной устранимой особой точки).

Теорема. Пусть функция f (z) аналитична на плоскости Ĉ, кроме конечного числа точек. Тогда сумма вычетов во всех особых точках, включая и точку 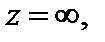равна нулю.

Пусть функция f (z) аналитична всюду на полуплоскости 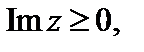кроме конечного числа особых точек, которые лежат сверху от действительной оси. Пусть также точка 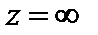является нулем кратности больше единицы функции f (z). Тогда справедлива формула

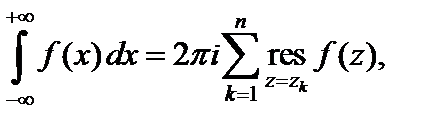(29.49)

где – особые точки функции f (z), в которых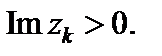

Пусть дробно-рациональная функция 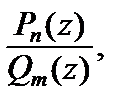где 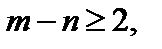является аналитической на действительной оси. Тогда

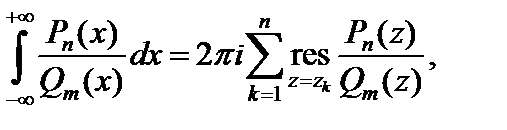(29.50)

где 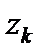– полюсы функции 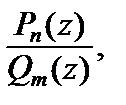которые лежат в полуплоскости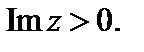

Если 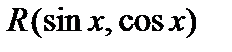– дробно-рациональная функция от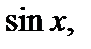 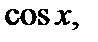то

Пример 1. Вычислить вычет функции:

1) 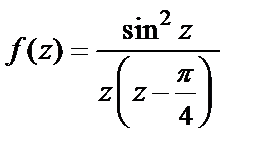в точке 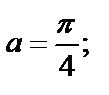2) 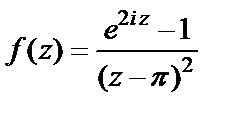в точке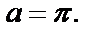

Решение. 1) Очевидно, что 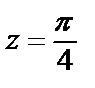есть простой полюс функции. Найти вычет в этой точке можно двумя способами: согласно формулам (29.43) и (29.44). Покажем это.

Используя формулу (29.43), получаем:

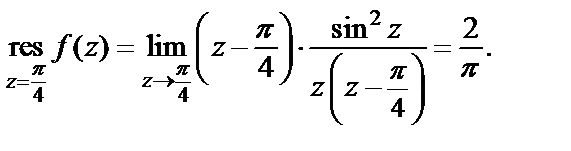
Заданная функция удовлетворяет всем условиям, при которых справедлива формула (29.44). Поэтому,

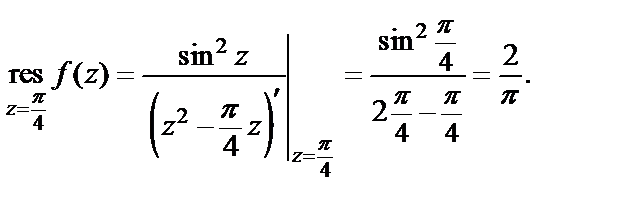
2) Поскольку, в соответствии с формулой Эйлера,

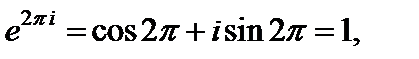
то числитель и знаменатель заданной функции зануляются в точке 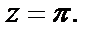Для выяснения характера особой точки 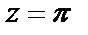разложим числитель в ряд Тейлора по степеням 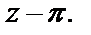Найдем коэффициенты этого ряда:

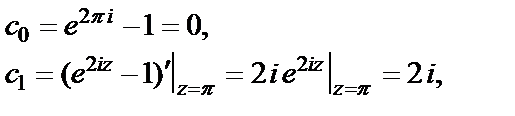
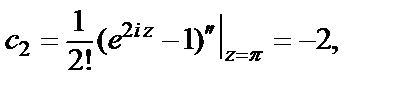
Получаем

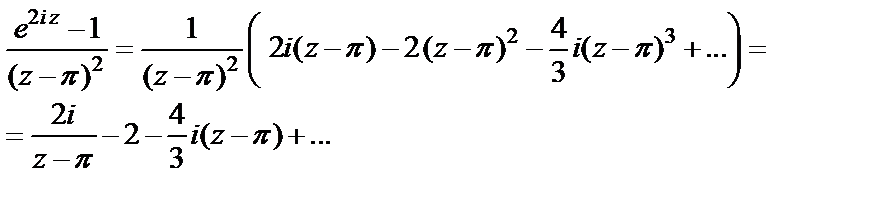
Видим, что 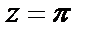– простой полюс данной функции. Однако использовать формулу (29.43) или (29.44) уже не надо. Из полученного разложения имеем:

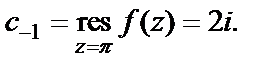
Пример 2. Вычислить вычет в точке 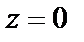функции:

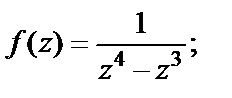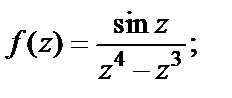1) 2) 3)

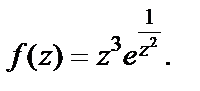
Решение. 1) Поскольку

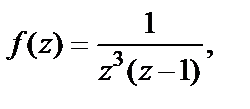
то 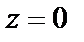есть полюс третьего порядка заданной функции. Тогда согласно формуле (29.45), при 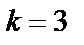имеем:

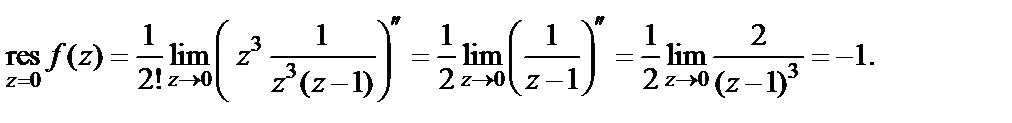
2) Запишем данную функцию в виде

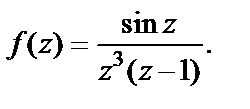(29.51)

Выражение (29.51) показывает, что точка 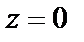есть нуль кратности три знаменателя. Однако в этой точке и числитель равен нулю, причем для него 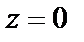есть простой нуль (это следует из разложения функции 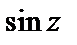в ряд Маклорена – формула (29.29)). Значит, в отличие от первой функции, рассмотренной в этом примере, точка 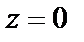есть полюс второго порядка. Для вычисления вычета в ней воспользуемся формулой (29.45) для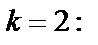

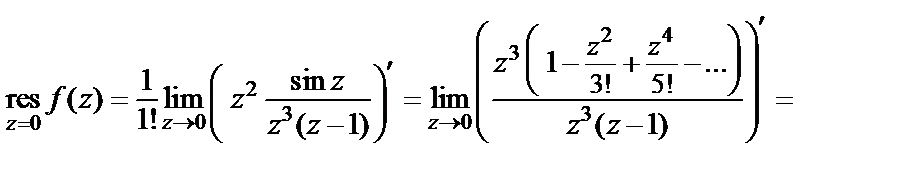
3) Чтобы определить характер особой точки 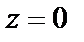для данной функции, лучше всего использовать разложение экспоненты в ряд Маклорена (29.29), заменив в нем z н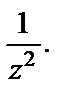а Тогда

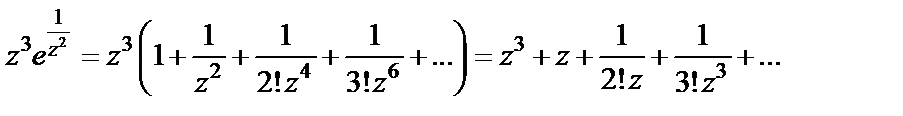
Видим, что коэффициент 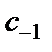равен 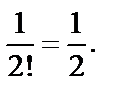Значит, 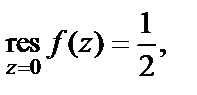причем точка 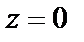существенно особая точка.

Пример 3. Вычислить интеграл от функции

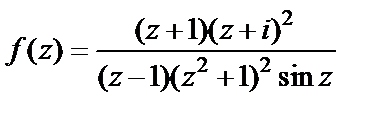
по положительно ориентированной окружности:

1) 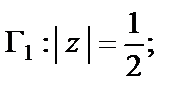2)

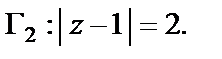
Решение. Найдем особые точки подынтегральной функции и определим их тип. Нули знаменателя – точки 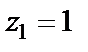(простой нуль);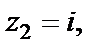 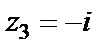(двукратные нули); 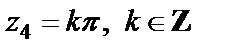(простые нули). С учетом того, что 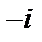– нуль кратности два числителя, приходим к заключению, что 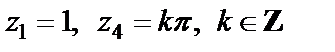– простые полюсы; 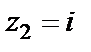– полюс второго порядка, 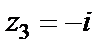– устранимая особая точка. Вычислим интеграл от данной функции, основываясь на формуле (29.46).

1) Внутри линии 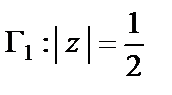находится только одна особая точка 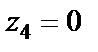(при ).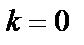

Используя формулы (29.46) и (29.43), получаем:

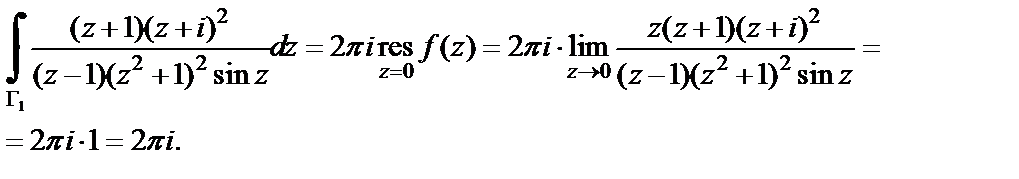
2) Линия 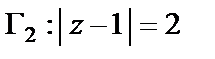имеет внутри четыре особые точки: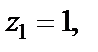 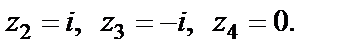Поэтому надо вычислить четыре вычета.

Поскольку 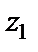– простой полюс, то по формуле (29.43) получаем:

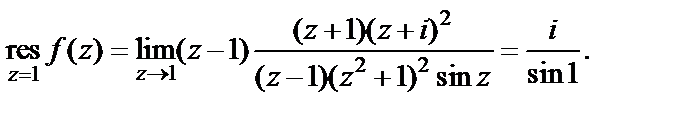
Для вычисления вычета в полюсе второго порядка 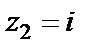воспользуемся формулой (29.45):

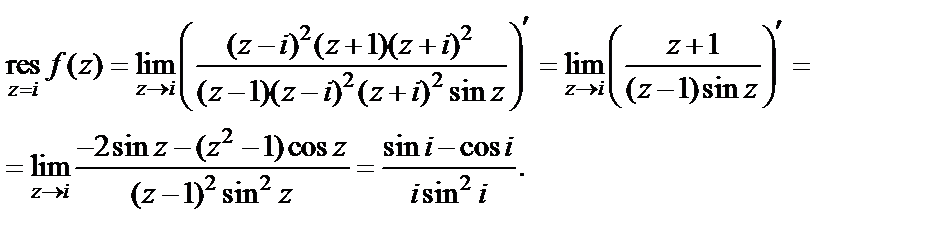
Поскольку 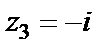– устранимая особая точка, то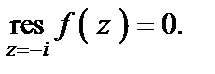

Вычет в точке 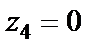находим, используя формулу (29.43). Получаем

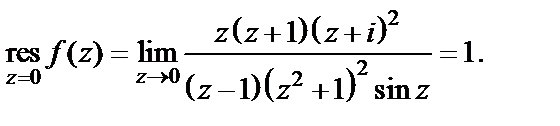
Воспользуемся теперь формулой (29.46) и полученными значениями вычетов:

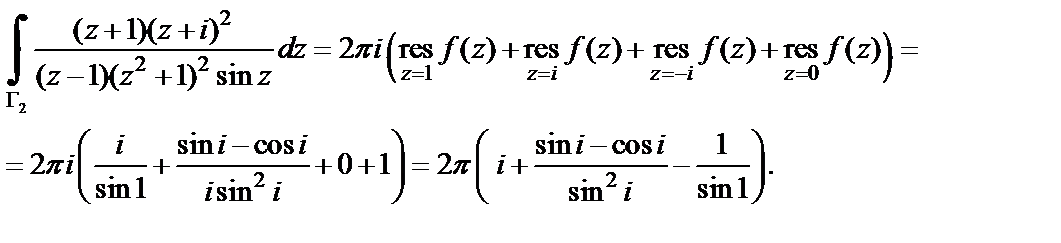
Пример 4. Вычислить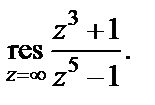

Решение. Преобразуем выражение, которое стоит под знаком вычета:

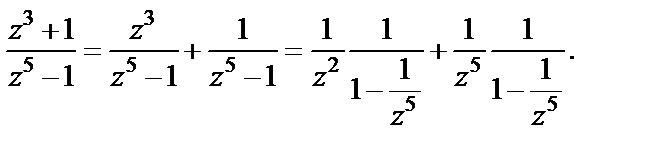
Теперь используем разложение (29.31):

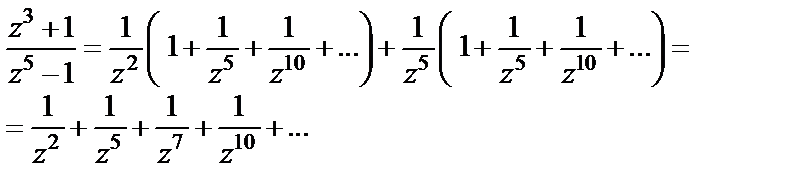
Видим, что 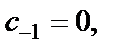т. е.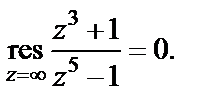

Пример 5. Вычислить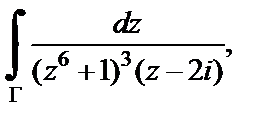

где Г – окружность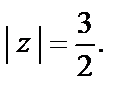

Решение. Внутри окружности 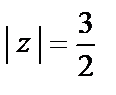лежат шесть полюсов третьего порядка, вне ее – простой полюс 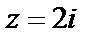и точка Очевидно, что более рационально вычислять сумму вычетов в точках 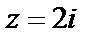и Согласно формуле (29.43), получаем:

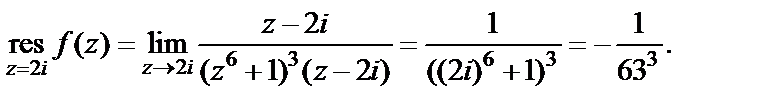
Для определения вычета в точке 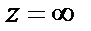найдем несколько слагаемых ряда Лорана. С этой целью сделаем замену переменной 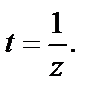Тогда

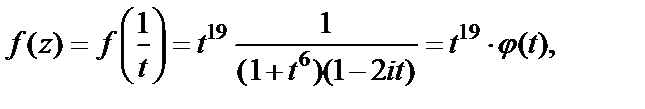
где через 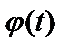обозначена аналитическая функция в окрестности точки 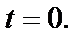Функцию 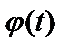можно разложить в степенной ряд:

Возвращаясь к старой переменной, имеем:

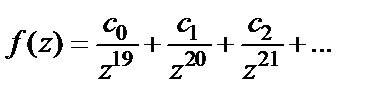
Видим, что 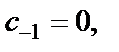т. е. 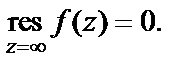Получили следующее значение интеграла:

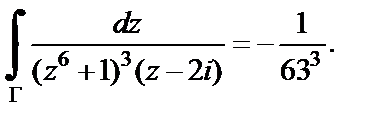
Пример 6. Вычислить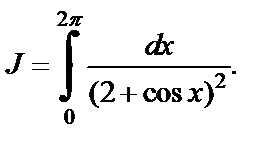

Решение. Сделаем замену переменной 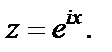Тогда

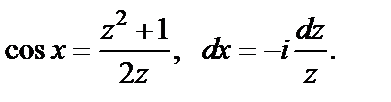
Приходим к необходимости вычисления интеграла

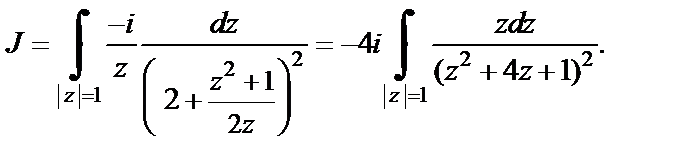
Найдем особые точки подынтегральной функции. Это те значения z, для которых 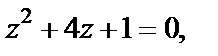т. е.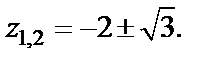

Внутри круга лежит только точка 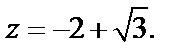Для подынтегральной функции она является полюсом второго порядка. Значит,

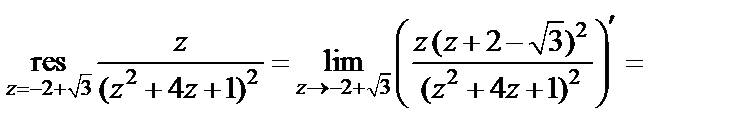
По формуле (29.46) получаем

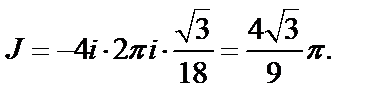
Пример 7. Вычислить интеграл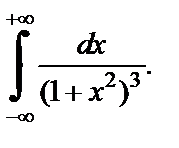

Решение. Функция 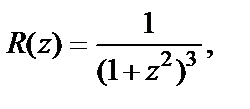которая является подынтегральной при 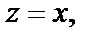удовлетворяет всем условиям, при которых справедлива формула (29.50). Ее особыми точками являются точки 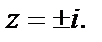Это полюсы третьего порядка. В верхней полуплоскости лежит только полюс а поэтому

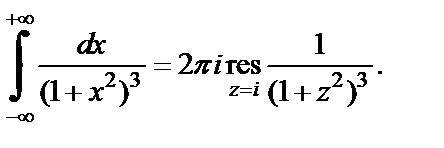
Находим

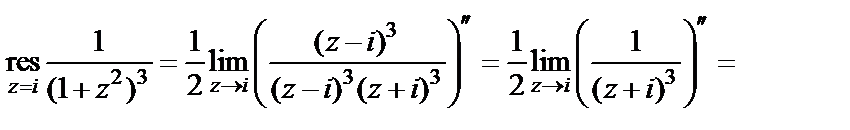
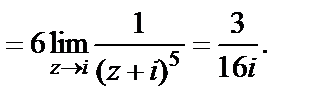
Получаем

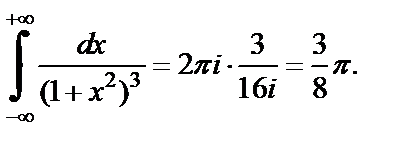
Date: 2015-07-24; view: 2219; Нарушение авторских прав