Справедливы формулы

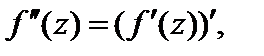
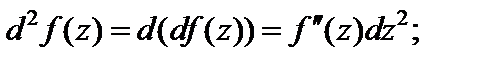
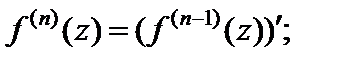
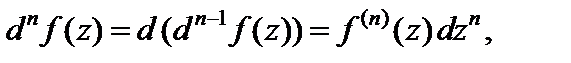
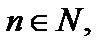
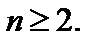
Функция 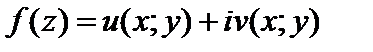является дифференцируемой в точке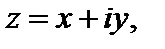 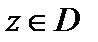тогда и только тогда, когда функции u, v являются дифференцируемыми в точке (x; y) и выполняются соотношения:

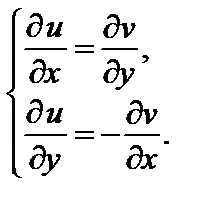(29.4)

Последние два равенства называют условиями Д’Аламбера–Эйлера (Коши–Римана).

Если все частные производные функций u, v непрерывны в точке (x, y) и удовлетворяют условиям Д’Аламбера–Эйлера, то функция 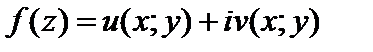является дифференцируемой в точке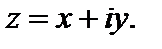

Если функция f (z) является дифференцируемой в точке 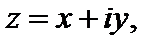то для вычисления ее производной в этой точке справедливы формулы:

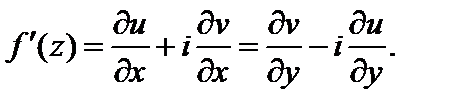(29.5)

Геометрический смысл модуля производной: модуль производной 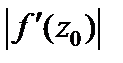в точке 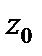можно рассматривать как коэффициент растяжения в точке 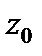при отображении

Геометрический смысл аргумента производной: аргумент производной 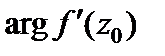в точке 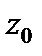есть угол поворота касательной к кривой в точке 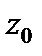при отображении

Взаимно-однозначное отображение, которое сохраняет углы между кривыми, проходящими через некоторую точку, и дает одинаковый коэффициент их растяжения, называется конформным в этой точке.

Функция называется аналитической в области D, если она однозначна и дифференцируема в каждой точке этой области. Функция f (z) называется аналитической в замкнутой области 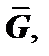если существует область в которой функция аналитична. Функция называется аналитической в точке, если существует некоторая окрестность этой точки, в которой функция аналитична.

Необходимыми и достаточными условиями аналитичности функции 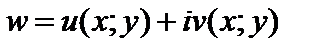в области D являются дифференцируемость в области D функций u, v и выполнение в этой области условий Д’Аламбера–Эйлера (29.4).

Однозначная функция u (x; y) двух действительных переменных называется гармонической в области D, если она имеет непрерывные частные производные до второго порядка включительно и удовлетворяет уравнению Лапласа:

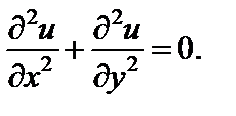(29.6)

Действительная и мнимая части аналитической функции являются гармоническими функциями. Условие гармоничности функций u (x; y) и v (x; y) является необходимым условием аналитичности функции 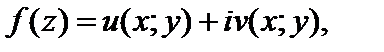но не является достаточным.

Пусть D – произвольная область плоскости Ĉ. Если для любой замкнутой линии 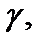которая принадлежит множеству D, внутренняя или внешняя область кривой 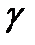целиком принадлежит D, то область D называется односвязной.

Область, границей которой является объединение конечного числа замкнутых непрерывных непересекающихся кривых без точек самопересечения, называется многосвязной. Если граница области состоит из n указанных кривых, то область называется n - связной.

Любая гармоническая в односвязной области D функция является действительной (мнимой) частью некоторой аналитической в области D функции. При этом вторая неизвестная часть этой функции находится с точностью до постоянного слагаемого по ее известной части.

Пример 1. Выяснить, дифференцируема ли функция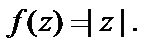

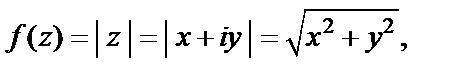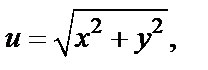
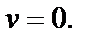Решение. Находим т. е. Проверим, выполняются ли условия (29.4) дифференцируемости функции.

Вычисляем

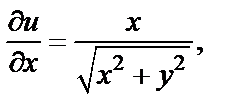
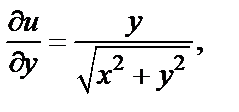
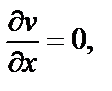
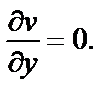
Видим, что условие 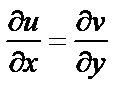выполняется при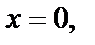 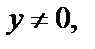а условие 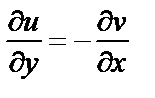– при 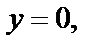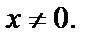Таким образом, сразу оба условия Д’Aламбера–Эйлера не выполняются ни в одной точке комплексной плоскости, т. е. функция 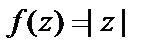не является дифференцируемой ни в одной точке.

Пример 2. Выяснить дифференцируемость функции f (z) и найти ее производную, если:

1) 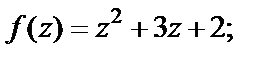2)

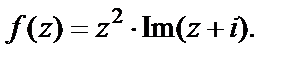
Решение. 1) 1-й способ. Функция определена в каждой точке плоскости C. Найдем ее действительную часть u, а также мнимую часть v.

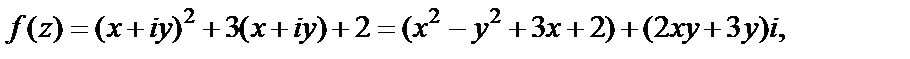
т. е. 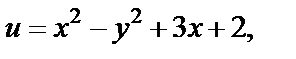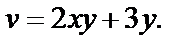Проверим, имеет ли эта функция непрерывные частные производные. Найдем их:

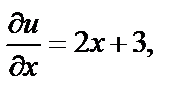
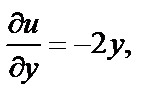
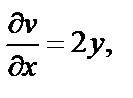
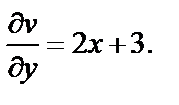
Видим, что все производные непрерывны на плоскости C и удовлетворяют на ней условиям Коши–Римана (29.4). Значит, функция f (z) является дифференцируемой на всей комплексной плоскости. Для вычисления ее производной можно использовать, например, формулу (29.5):

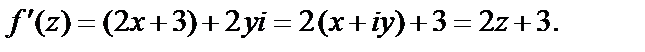
2-й способ. Используя формулу 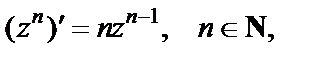и правила дифференцирования (29.3), получим 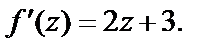Очевидно, что этот способ нахождения производной рациональнее, чем первый.

2) Функция определена на всей плоскости C. Найдем ее действительную и мнимую части, преобразовав выражение, которым она задается (при условии ):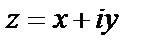

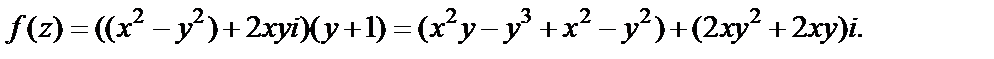
Тогда

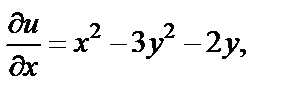
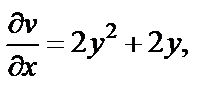
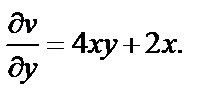
Частные производные непрерывны всюду на множестве C, но нельзя утверждать, что условия Коши–Римана выполняются для всех 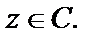Найдем те точки, где они справедливы, т. е. где имеет решение система

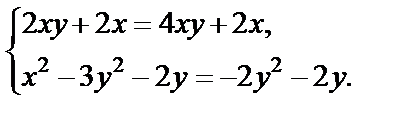
Поскольку она равносильна системе

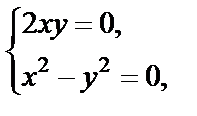
то видим, что условия Коши–Римана выполняются только в точке (0; 0). Для этой точки все частные производные равны нулю, значит,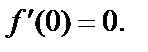

Пример 3. Найти коэффициент растяжения и угол поворота при отображении 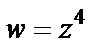в точке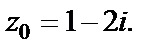

Решение.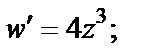

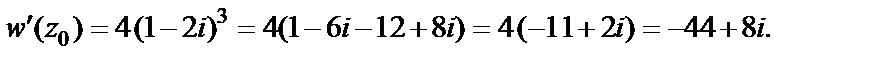
Откуда получаем коэффициент растяжения в заданной точке:

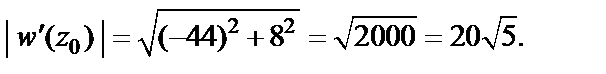
Находим угол поворота для заданного отображения:

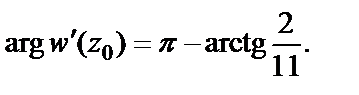
Пример 4. Найти область аналитичности функции:

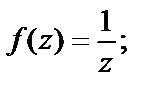1) 2) 3)

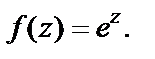
Решение. 1) Поскольку 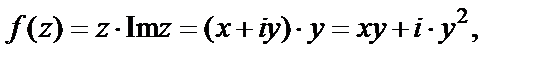то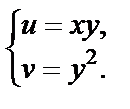

Тогда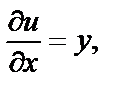

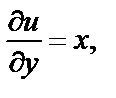
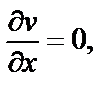
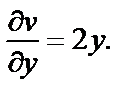
Условия Д’Аламбера–Эйлера (29.4) выполняются в единственной точке 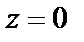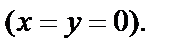В этой точке функция является дифференцируемой, но не является аналитической. Таким образом, функция 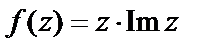не является аналитической ни в одной точке комплексной плоскости.

2) Найдем действительную и мнимую части заданной функции:

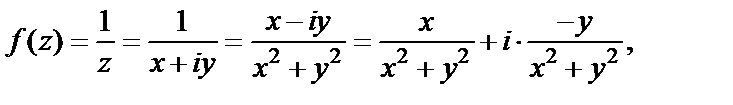т. е.

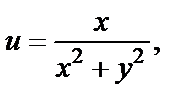
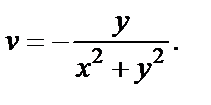
Находим частные производные:

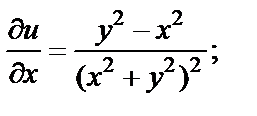
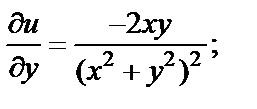
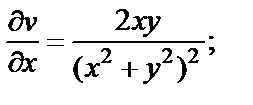
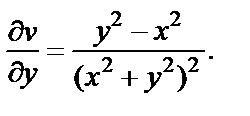
Условия Д’Aламбера–Эйлера (29.4) выполняются во всех точках, кроме точки 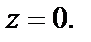Функция 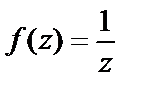аналитична на всей комплексной плоскости, кроме точки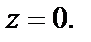

3) Для нахождения действительной и мнимой частей заданной функции используем формулы Эйлера:

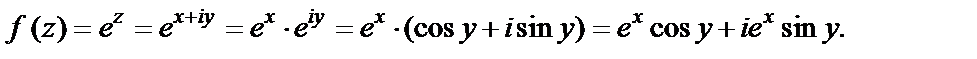
Поэтому

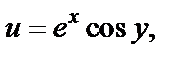
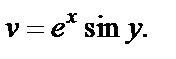
Вычисляем

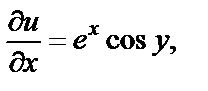
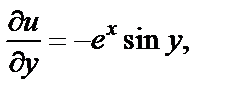
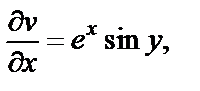
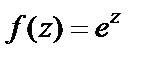Замечаем, что условия дифференцируемости (29.4) выполняются для всех т. е. функция аналитична на всей комплексной плоскости.

Пример 5. Восстановить аналитическую функцию f (z) по ее известной части (если это возможно): 1) действительной 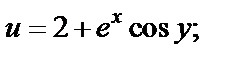2) мнимой 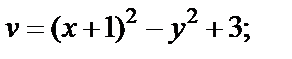3) действительной

Решение. 1) Убедимся, что функция u (x, y) является гармонической. Поскольку

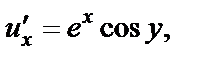
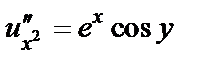и 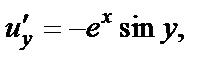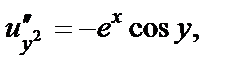то справедливо равенство (29.6). Первое равенство из условий Коши–Римана (т. е. 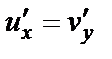) приобретает вид откуда после интегрирования имеем

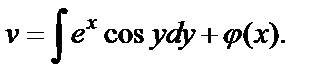
Таким образом, приходим к выражению

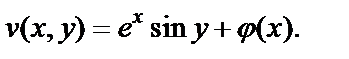
Из второго равенства Коши–Римана 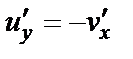имеем: 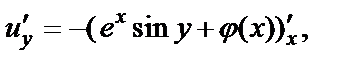или, то же самое,

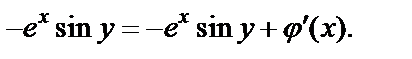
Из последнего равенства получаем 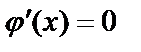и соответственно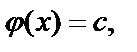 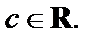В результате найдена функция 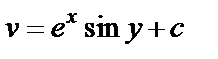и восстановлена аналитическая функция

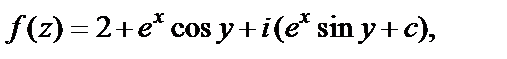которую можно записать иначе:

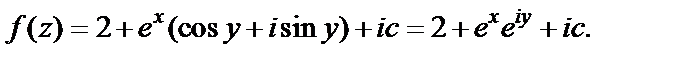
Это то же самое, что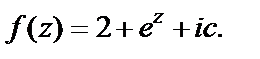

2) Нетрудно убедиться, что функция v (x, y) является гармонической, так как

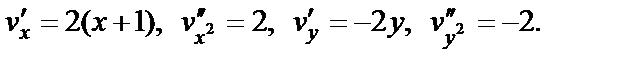
Равенство 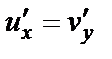из условий Коши–Римана принимает вид 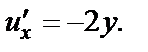Интегрируя его, находим

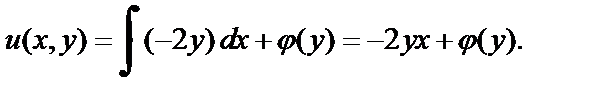
Второе равенство 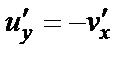из тех же условий дает

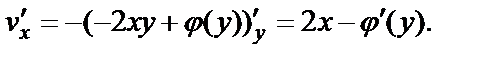Значит,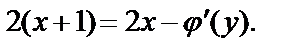

Из последнего равенства получаем 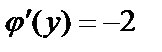и соответственно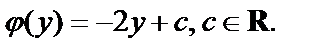

Таким образом, 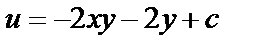и

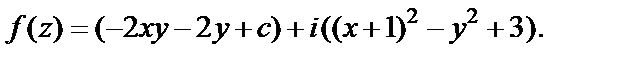
Функцию f (z) можно записать в виде зависимости от z. Действительно,

что приводит к виду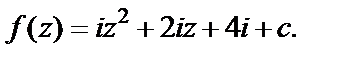

3) Проверим, является ли функция 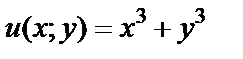гармонической. Вычислим соответствующие частные производные:

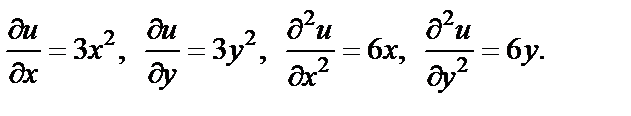
Уравнение Лапласа (29.6) для этой функции приобретает вид 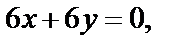откуда видим, что функция удовлетворяет уравнению Лапласа только в точках прямой 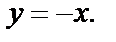Приходим к заключению, что она не является гармонической, так как не существует области, в которой справедливо равенство (29.6). По этой причине не существует аналитической функции, у которой действительная часть есть

Date: 2015-07-24; view: 1076; Нарушение авторских прав