
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Справедливы утверждения
|
|
1. Пусть 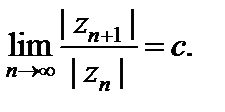 Если
Если  то ряд
то ряд 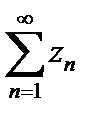 сходится абсолютно, если
сходится абсолютно, если 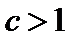 – ряд расходится.
– ряд расходится.
2. Пусть 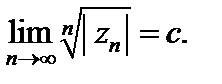 Если
Если 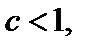 то ряд
то ряд 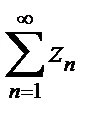 сходится абсолютно, если
сходится абсолютно, если 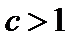 – ряд расходится.
– ряд расходится.
3. Если ряд 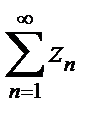 сходится абсолютно, то он сходится.
сходится абсолютно, то он сходится.
З а м е ч а н и е. Из сходимости ряда не следует его абсолютная сходимость.
Абсолютная сходимость ряда с комплексными элементами равнозначна абсолютной сходимости его действительной и мнимой частей.
Ряд вида
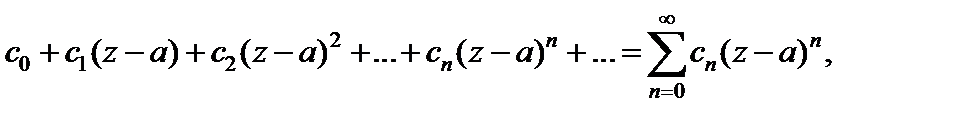 (29.24)
(29.24)
где 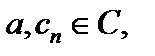
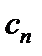 – коэффициенты ряда,
– коэффициенты ряда, 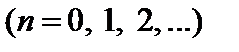
называется степенным рядом.
Теорема Абеля. Если степенной ряд 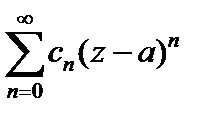 сходится в некоторой точке
сходится в некоторой точке 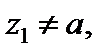 то он сходится, причем абсолютно, в любой точке z, которая удовлетворяет условию
то он сходится, причем абсолютно, в любой точке z, которая удовлетворяет условию
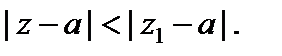
Если этот ряд расходится в некоторой точке 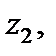 то он расходится во всех точках z, для которых
то он расходится во всех точках z, для которых
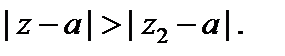
Пусть ряд 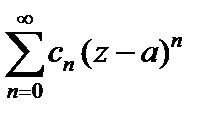 сходится более чем в одной точке, но не на всей комплексной плоскости. Тогда существует действительное число r такое, что этот ряд абсолютно сходится для всех z, для которых
сходится более чем в одной точке, но не на всей комплексной плоскости. Тогда существует действительное число r такое, что этот ряд абсолютно сходится для всех z, для которых 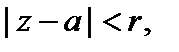 и расходится для тех z, для которых
и расходится для тех z, для которых 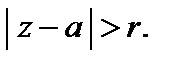 При этом круг
При этом круг 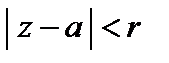 называется кругом сходимости, число r – радиусом сходимости степенного ряда.
называется кругом сходимости, число r – радиусом сходимости степенного ряда.
Пусть функция f (z) является аналитической в круге 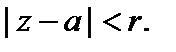 Тогда внутри этого круга функция f (z) разлагается в степенной ряд по степеням
Тогда внутри этого круга функция f (z) разлагается в степенной ряд по степеням 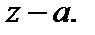 Такое разложение единственно.
Такое разложение единственно.
Признаки Д’Aламбера и Коши. Если существует
 (29.25)
(29.25)
или соответственно
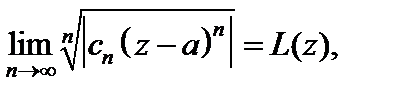 (29.26)
(29.26)
то ряд (29.24) сходится абсолютно во всех точках z, для которых 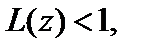 и расходится, если
и расходится, если 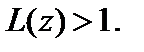
Степенной ряд вида
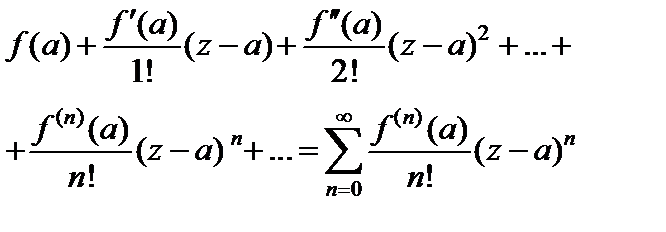 (29.27)
(29.27)
называется рядом Тейлора функции f (z), 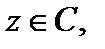 в окрестности точки a.
в окрестности точки a.
Функция f (z), аналитическая в круге 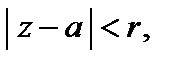 разлагается в этом круге в ряд Тейлора:
разлагается в этом круге в ряд Тейлора:
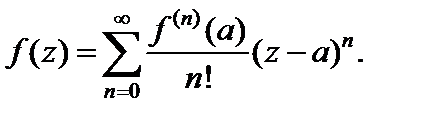 (29.28)
(29.28)
С учетом формулы (29.22), равенство (29.28) можно записать в виде
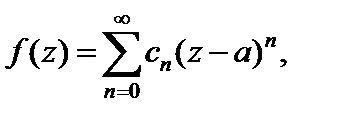
где 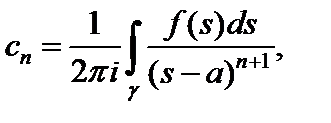
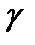 – окружность
– окружность 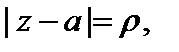

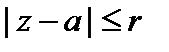 – круг аналитичности f (z).
– круг аналитичности f (z).
Ряд Тейлора (29.28), у которого 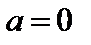 называется рядом Маклорена.
называется рядом Маклорена.
Общий вид ряда Маклорена:
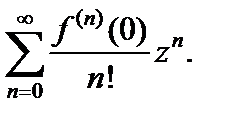
Разложения в ряд Маклорена основных элементарных функций:

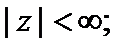
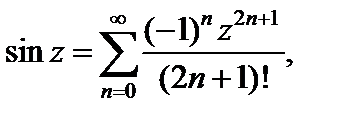
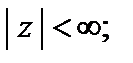 (29.29)
(29.29)
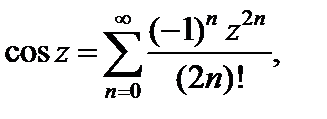
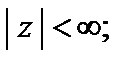 (29.30)
(29.30)
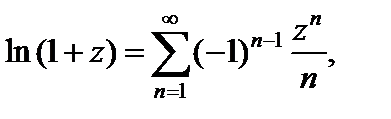
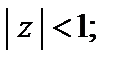
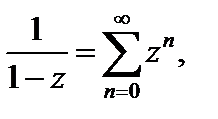
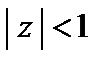 – геометрический ряд. (29.31)
– геометрический ряд. (29.31)
Ряд вида
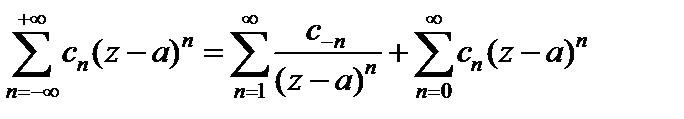 (29.32)
(29.32)
называется рядом Лорана, причем 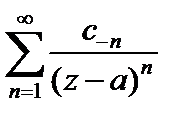 называется главной частью ряда Лорана, а
называется главной частью ряда Лорана, а 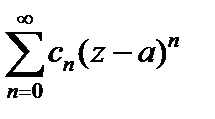 – правильной частью ряда Лорана.
– правильной частью ряда Лорана.
Функция f (z), аналитическая в кольце 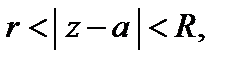 разлагается в этом кольце в абсолютно сходящийся ряд Лорана
разлагается в этом кольце в абсолютно сходящийся ряд Лорана
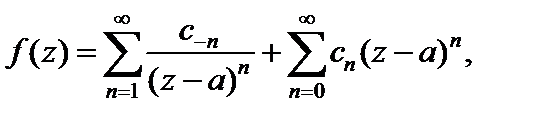 (29.33)
(29.33)
где коэффициенты определяются формулами:
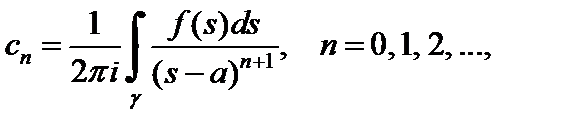
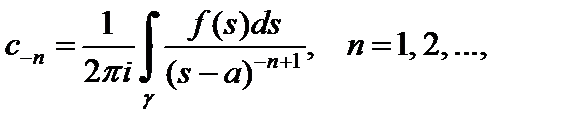
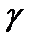 – окружность
– окружность 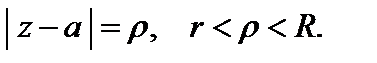
Разложение (29.33) в кольце 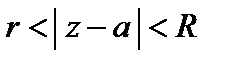 является единственным.
является единственным.
Заметим, что формулы для нахождения коэффициентов 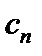 и
и 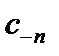 можно объединить в одну:
можно объединить в одну:
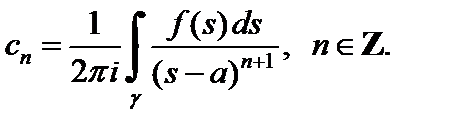
Пример 1. Исследовать сходимость ряда:
1) 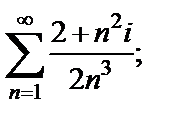 2)
2) 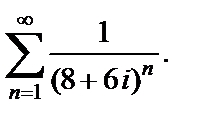
Решение. 1) 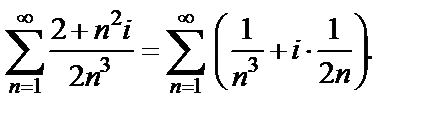 Рассмотрим ряды
Рассмотрим ряды 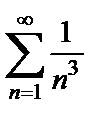 и
и 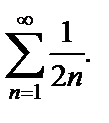 Ряд
Ряд 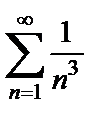 сходится, так как это обобщенный гармонический ряд
сходится, так как это обобщенный гармонический ряд  с
с 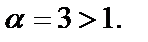 Ряд
Ряд 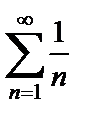 расходится (это гармонический ряд). Значит,
расходится (это гармонический ряд). Значит, 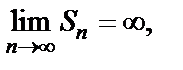 где
где 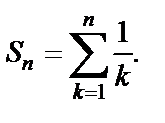 Так как
Так как 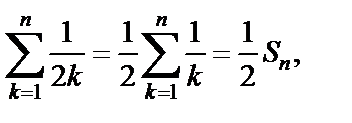 то
то 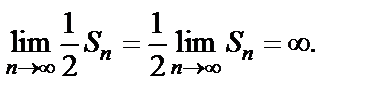
Отсюда следует, что ряд 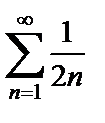 расходится, и, значит, исходный ряд
расходится, и, значит, исходный ряд 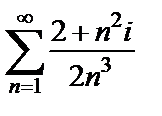 расходится.
расходится.
2) Ряд 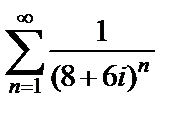 исследуем на абсолютную сходимость, для чего рассмотрим
исследуем на абсолютную сходимость, для чего рассмотрим 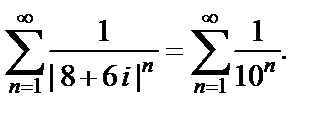
Последний ряд сходится (сходящаяся геометрическая прогрессия с 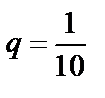 ). Значит, ряд
). Значит, ряд 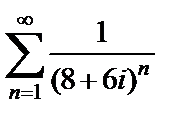 сходится абсолютно.
сходится абсолютно.
Пример 2. Исследовать на сходимость ряд:
1) 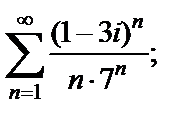 2)
2) 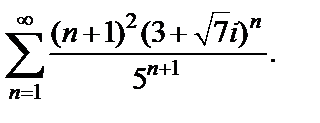
Решение. 1) Рассмотрим ряд из модулей его элементов:
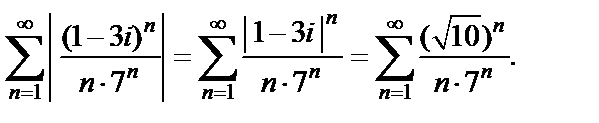
Для выяснения вопроса сходимости полученного знакоположительного ряда используем признак Коши:
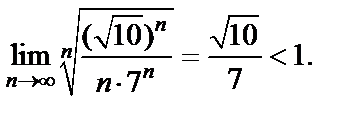
Это значит, что данный ряд сходится абсолютно, а поэтому сходится.
2) Исследование на сходимость ряда из модулей
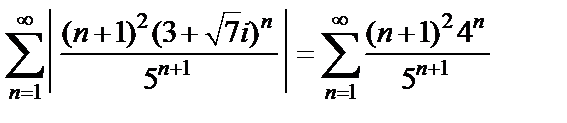
проведем на основе признака Д’Aламбера:
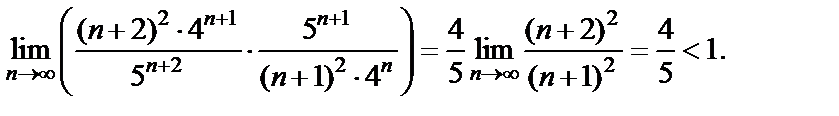
Последнее означает абсолютную сходимость данного ряда, чем гарантируется его сходимость.
Пример 3. Исследовать на сходимость ряд
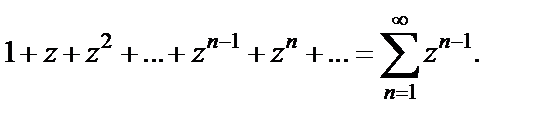
Решение. Функции-слагаемые 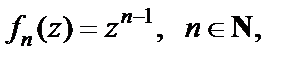 данного ряда определены на всей плоскости C. Его n- я частичная сумма есть
данного ряда определены на всей плоскости C. Его n- я частичная сумма есть
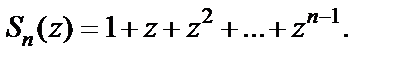
Методом математической индукции нетрудно убедиться в том, что
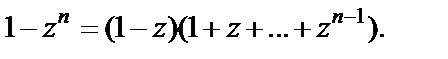
Тогда
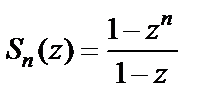
или, то же самое,
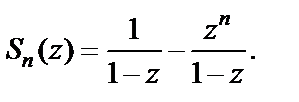
Если 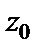 – произвольное комплексное число, то данный функциональный ряд преобразуется в числовой с частичной суммой
– произвольное комплексное число, то данный функциональный ряд преобразуется в числовой с частичной суммой
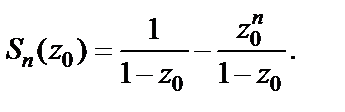
Поэтому, 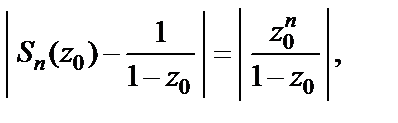
откуда 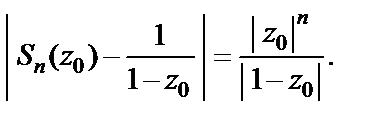
Из последнего отношения видно, что только для того числа 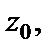 для которого
для которого 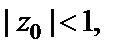 выполняется условие
выполняется условие
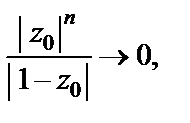 когда
когда 
Это означает, что
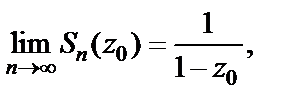 если
если 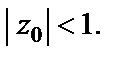
Произвольность числа 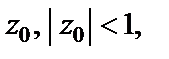 приводит к заключению, что внутри круга
приводит к заключению, что внутри круга 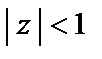 ряд сходится к сумме
ряд сходится к сумме 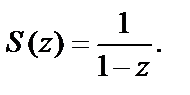
Если 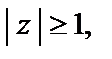 то общий элемент
то общий элемент 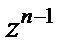 данного ряда не стремится к нулю с ростом n (необходимый признак сходимости не выполняется), а потому ряд расходится.
данного ряда не стремится к нулю с ростом n (необходимый признак сходимости не выполняется), а потому ряд расходится.
Таким образом, получена формула
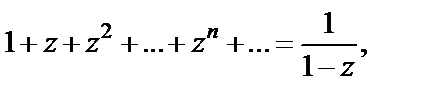 где
где 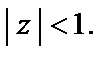
В заключение заметим, что полученный результат полностью соответствует действительному случаю, где для суммы бесконечно убывающей геометрической прогрессии имеем 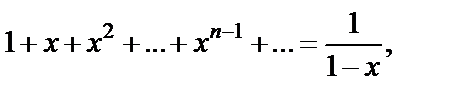 если
если 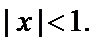
Пример 4. Найти множество абсолютной сходимости ряда
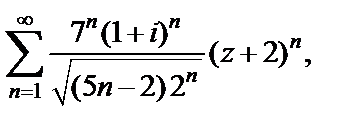 пользуясь признаком Д’Aламбера.
пользуясь признаком Д’Aламбера.
Решение. Используя формулу (29.25), получим:
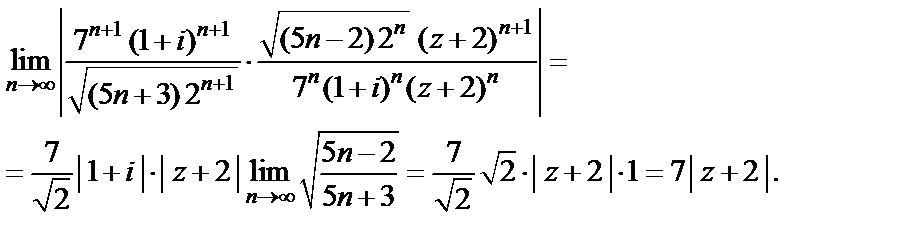
Если 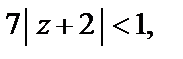 то ряд является абсолютно сходящимся. Очевидно, что это имеет место внутри круга
то ряд является абсолютно сходящимся. Очевидно, что это имеет место внутри круга 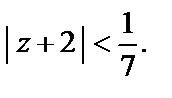 Одновременно с этим признак Д’Aламбера утверждает, что вне круга (т. е. при
Одновременно с этим признак Д’Aламбера утверждает, что вне круга (т. е. при 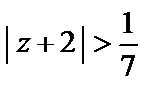 ) ряд расходится, однако он не достаточно «сильный», чтобы дать ответ о сходимости в точках окружности
) ряд расходится, однако он не достаточно «сильный», чтобы дать ответ о сходимости в точках окружности 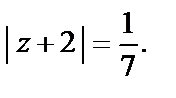
Пример 5. Найти круг и радиус сходимости степенного ряда 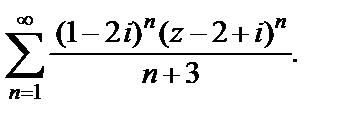
Решение. Используем признак Д'Аламбера и рассмотрим предел 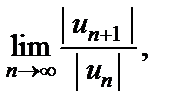 т. е.
т. е.
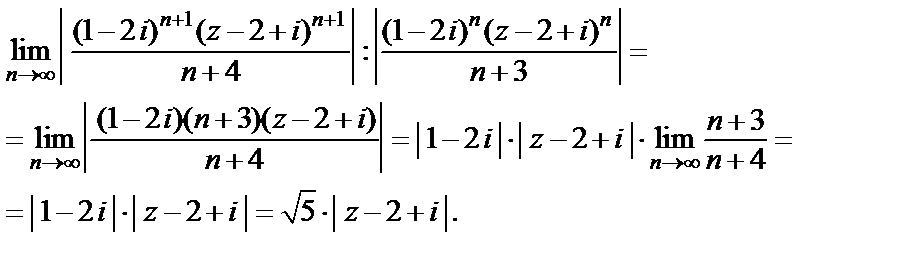
По признаку Д'Аламбера ряд сходится, если
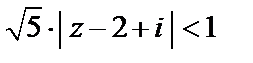 или
или 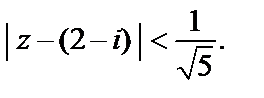
Значит, круг сходимости есть  радиус сходимости
радиус сходимости 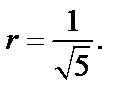
Пример 6. Разложить в ряд Тейлора по степеням 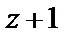 функцию:
функцию:
1) 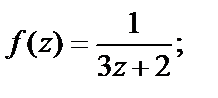 2)
2) 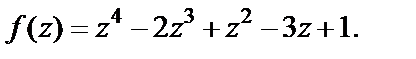
Найти область сходимости полученного ряда.
Решение. 1) Решим задачу двумя способами.
1-й способ. Используем формулу (29.28) для 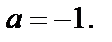 Для этого найдем производные функции и их значения в точке
Для этого найдем производные функции и их значения в точке 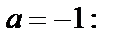

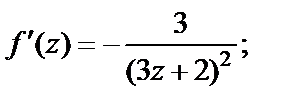
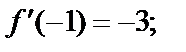
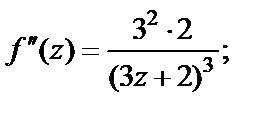
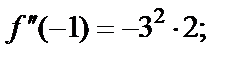
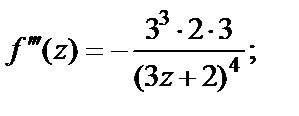
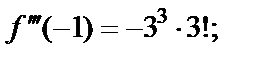
………………………… ……………………
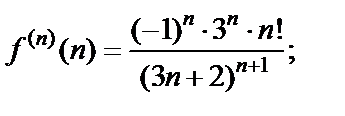
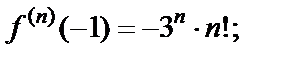
………………………… ……………………
Тогда получаем
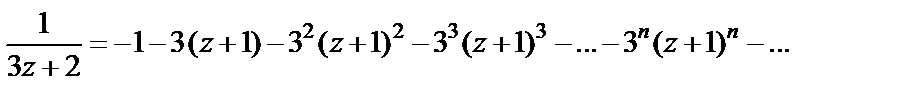
Радиус сходимости полученного ряда найдем согласно формуле
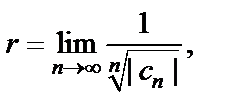
т. е. 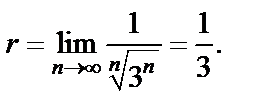
Значит, ряд сходится внутри круга 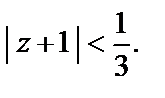
2-й способ. Запишем выражение, которое задает функцию f (z), в другом виде:
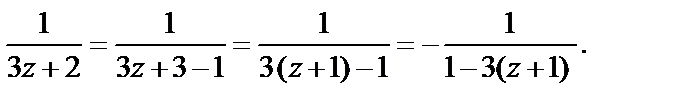
Полученную дробь рассмотрим как сумму геометрической прогрессии со знаменателем 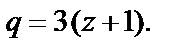
Если 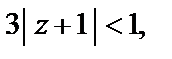 то
то
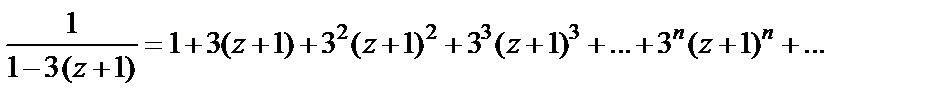
Поэтому заданная функция раскладывается в ряд того же вида, который мы получили первым способом.
2) Для того чтобы получить разложение функции
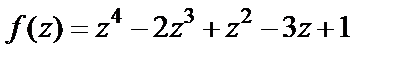 в ряд Тейлора на основе формулы (29.28), вычислим значения ее производных в точке
в ряд Тейлора на основе формулы (29.28), вычислим значения ее производных в точке 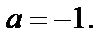 Сразу заметим, что данная функция есть многочлен 4-й степени, а поэтому все производные, начиная с пятой, будут равны нулю. Получаем
Сразу заметим, что данная функция есть многочлен 4-й степени, а поэтому все производные, начиная с пятой, будут равны нулю. Получаем
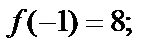
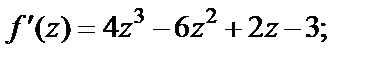
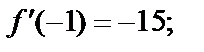

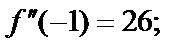
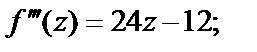
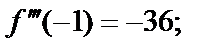
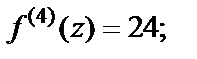

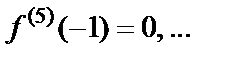
Тогда
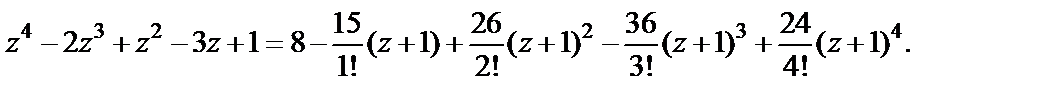
Логично, что для многочлена 4-й степени ряд Тейлора приобретает вид тоже многочлена 4-й степени. И это равенство справедливо на всей комплексной плоскости.
Пример 7. Найти круг сходимости ряда 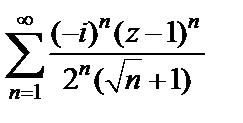 и исследовать его сходимость в точках
и исследовать его сходимость в точках 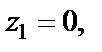
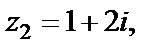
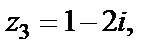
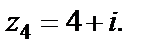
Решение. Рассмотрим ряд из модулей членов, т. е. 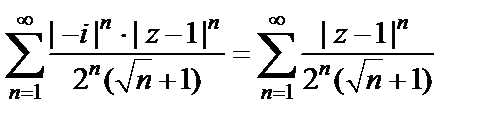 и вычислим предел
и вычислим предел 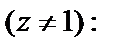
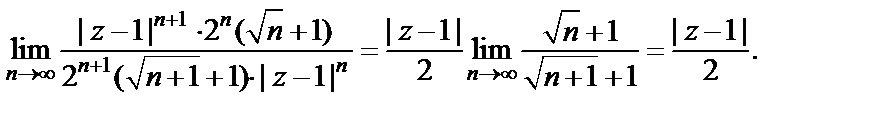
Значит, по признаку Д’Aламбера, круг сходимости определяется неравенством 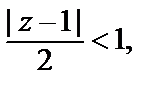 т. е.
т. е. 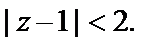
Для 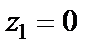 имеем
имеем 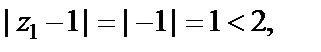 т. е. точка
т. е. точка 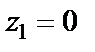 лежит внутри круга сходимости, значит, исходный ряд в этой точке сходится абсолютно.
лежит внутри круга сходимости, значит, исходный ряд в этой точке сходится абсолютно.
Для 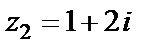 получаем
получаем 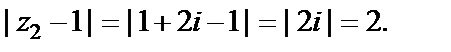
Точка 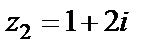 лежит на границе круга сходимости. Из общей теории необходимо сделать вывод о сходимости ряда в этой точке. Исследуем числовой ряд, который получается из исходного степенного ряда при значении
лежит на границе круга сходимости. Из общей теории необходимо сделать вывод о сходимости ряда в этой точке. Исследуем числовой ряд, который получается из исходного степенного ряда при значении 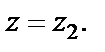 Имеем ряд
Имеем ряд
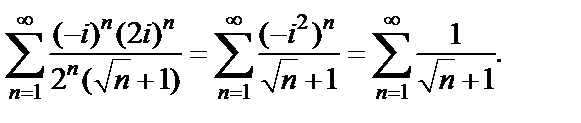
Ряд 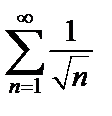 расходится (как ряд Дирихле с
расходится (как ряд Дирихле с 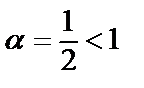 ). Применяя предельный признак сравнения, делаем вывод, что ряд
). Применяя предельный признак сравнения, делаем вывод, что ряд 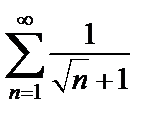 расходится. Исходный ряд в точке
расходится. Исходный ряд в точке 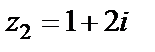 расходится.
расходится.
Для 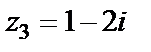 имеем
имеем 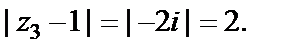
Точка 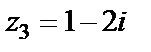 лежит на окружности, ограничивающей круг сходимости. При
лежит на окружности, ограничивающей круг сходимости. При 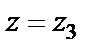 исходный ряд имеет вид
исходный ряд имеет вид
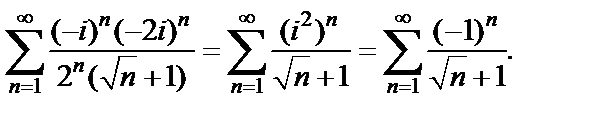
Этот ряд не сходится абсолютно (как было показано выше), но он является знакочередующимся и для него выполняются оба условия теоремы Лейбница. По признаку Лейбница этот ряд сходится условно. Исходный ряд в точке 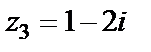 сходится.
сходится.
Для 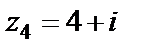 выполняется
выполняется 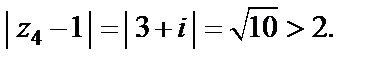 Значит, точка
Значит, точка  лежит вне круга сходимости, и поэтому исходный ряд в этой точке расходится.
лежит вне круга сходимости, и поэтому исходный ряд в этой точке расходится.
Пример 8. Разложить в ряд Маклорена функцию:
1) 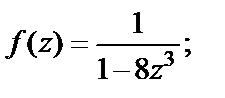 2)
2) 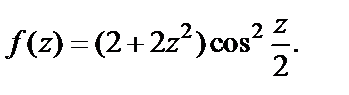
Решение. 1) Используем формулу (29.31), заменяя в ней переменную z на 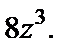 Тогда ряд Маклорена примет вид
Тогда ряд Маклорена примет вид
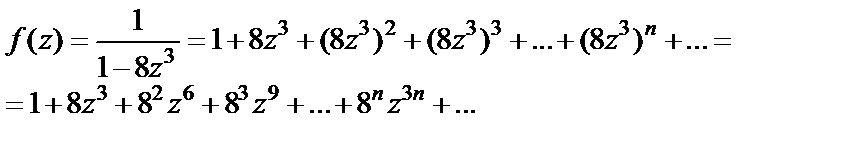
Он сходится при условии  т. е. внутри круга
т. е. внутри круга 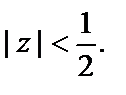
2) Сначала понизим степень косинуса:
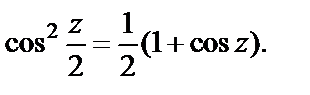
Далее, используя разложение (29.30), получим:
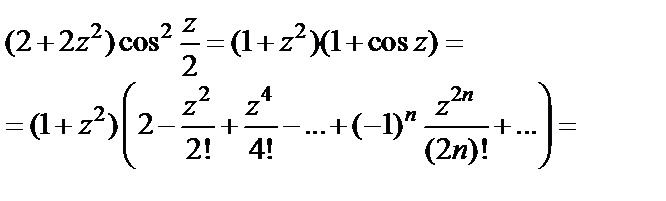
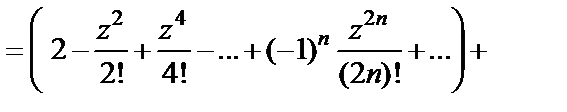
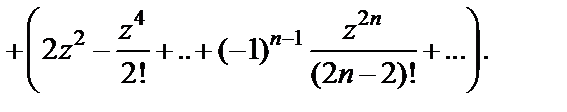
Приводя подобные, приходим к ответу
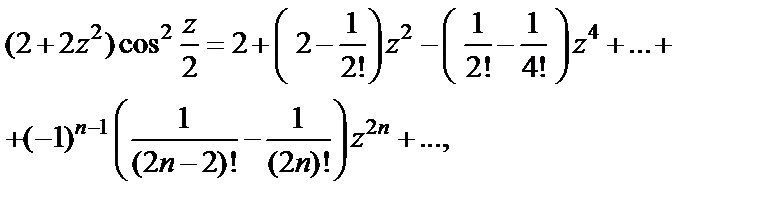
что ряд сходится на всей плоскости C.
Пример 9. Разложить в ряд Тейлора в окрестности точки 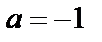 функцию
функцию 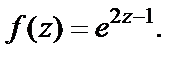
Решение. Этот пример можно решить согласно общему подходу, основываясь на формуле (29.28). Мы же используем ряд Маклорена (29.29). Для этого сделаем следующие преобразования:
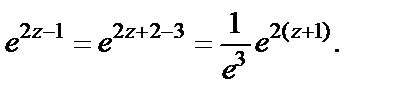
Тогда
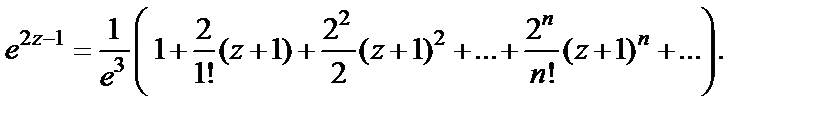
Ряд сходится на всей комплексной плоскости.
Пример 10. Найти область сходимости ряда
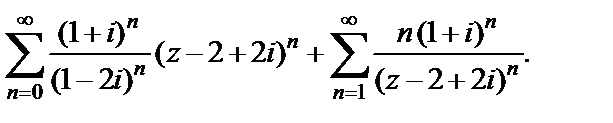
Решение. Данный ряд есть сумма рядов по положительным и отрицательным степеням разности 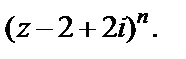 Для первого ряда (как для степенного) используем признак Коши:
Для первого ряда (как для степенного) используем признак Коши:
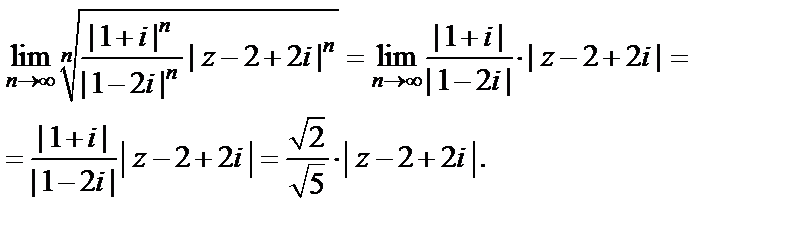
Ряд сходится, если 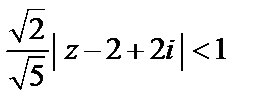 или, то же самое,
или, то же самое, 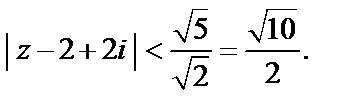
Значит, первый ряд сходится внутри круга:
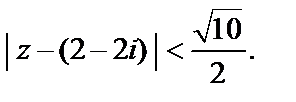
Для второго ряда применим признак Д’Aламбера:
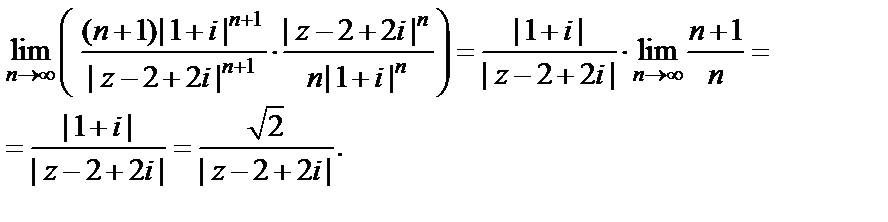
Ряд сходится, если
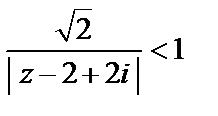 или
или 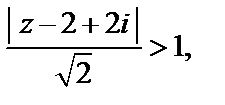 т. е.
т. е. 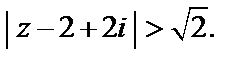
Полученные множества сходимости пересекаются, в результате чего мы имеем область сходимости данного ряда – кольцо

Пример 11. Разложить в ряд Лорана функцию
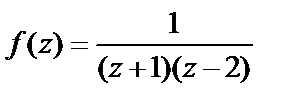 по степеням z.
по степеням z.
Решение. Нетрудно увидеть, что 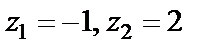 – особые точки данной функции. Это означает, что существуют три области, внутри которых функция аналитична:
– особые точки данной функции. Это означает, что существуют три области, внутри которых функция аналитична: 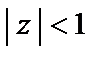 (область
(область 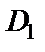 );
); 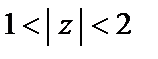 (область
(область 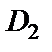 );
); 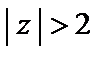 (область
(область 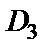 ) (рис. 29.3).
) (рис. 29.3).
| х |
| у |
| –1 |
| D 1 |
| D 2 |
| D 3 |
Рис. 29.3
В каждой из трех областей функция f (z) будет представляться своим рядом Лорана. Запишем функцию сначала в виде

Рассмотрим область 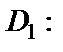
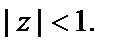 Представим функцию
Представим функцию
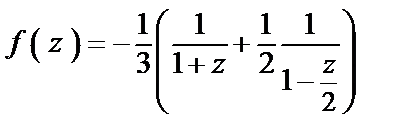 как сумму соответствующих геометрических прогрессий (имеем право сделать это, так как в области
как сумму соответствующих геометрических прогрессий (имеем право сделать это, так как в области 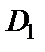 выполняется
выполняется 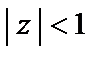 и
и 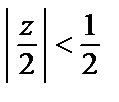 ). Тогда по формуле суммы (см. формулу (29.31)) получаем следующее представление функции рядом Лорана
). Тогда по формуле суммы (см. формулу (29.31)) получаем следующее представление функции рядом Лорана
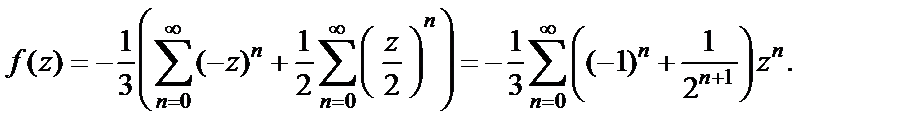
Видим, что ряд Лорана в области 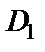 содержит только правильную часть, т. е. имеет вид степенного. Это не случайно, так как мы рассматриваем разложение в круге
содержит только правильную часть, т. е. имеет вид степенного. Это не случайно, так как мы рассматриваем разложение в круге 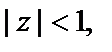 в котором функция аналитична.
в котором функция аналитична.
Рассмотрим область 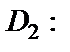
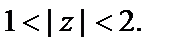 Тогда имеет смысл записать функцию в виде
Тогда имеет смысл записать функцию в виде
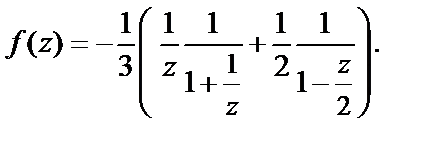
Так как в области 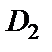 выполняется
выполняется 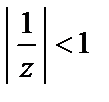 и
и 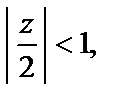 поэтому, по формуле суммы геометрического ряда, имеем разложение
поэтому, по формуле суммы геометрического ряда, имеем разложение
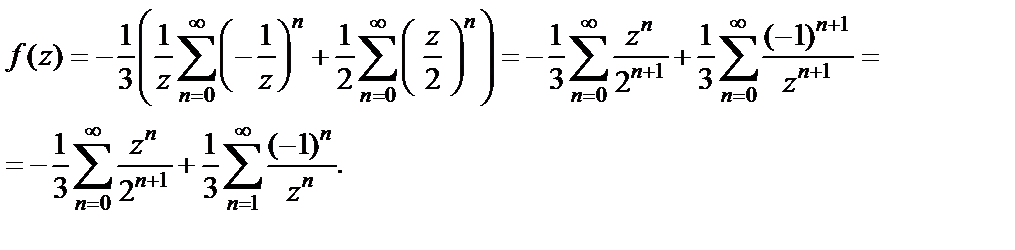
Полученный ряд Лорана содержит и правильную, и главную части.
Рассмотрим область 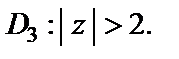 Функцию f (z) запишем в виде
Функцию f (z) запишем в виде 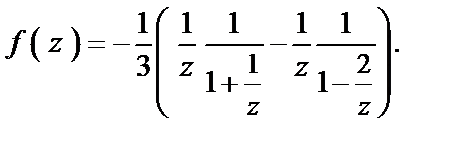 Поскольку в области
Поскольку в области 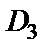 выполняется
выполняется 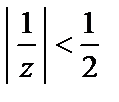 и
и 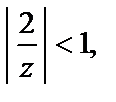 то на основе формулы суммы геометрического ряда получаем следующее разложение:
то на основе формулы суммы геометрического ряда получаем следующее разложение:
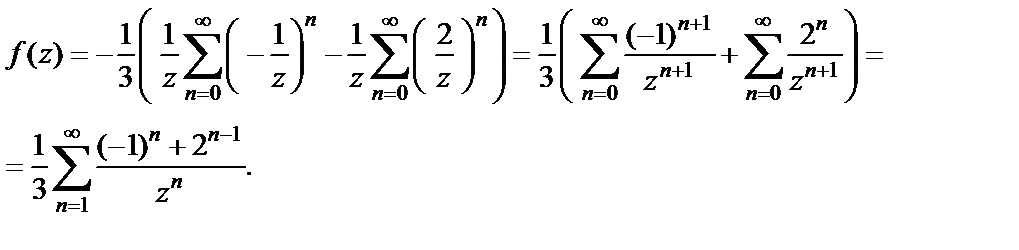
Замечаем, что полученный ряд Лорана содержит только главную часть.
Пример 12. Разложить функцию 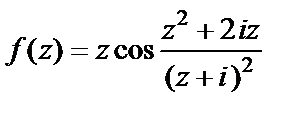 в ряд Лорана по степеням
в ряд Лорана по степеням 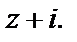
Решение. Точка 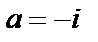 – единственная (на плоскости C) особая точка данной функции. Это означает, что можно построить кольцо
– единственная (на плоскости C) особая точка данной функции. Это означает, что можно построить кольцо 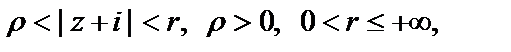 в котором функция является аналитической. Преобразуем выражение:
в котором функция является аналитической. Преобразуем выражение:
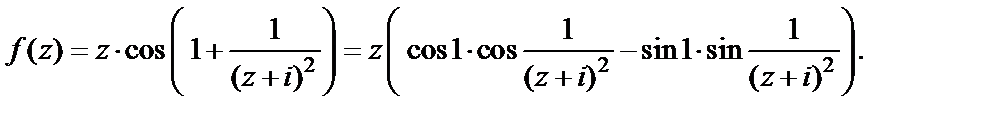
Далее используем разложения в ряд Маклорена (29.29) и (29.30), в которых вместо z возьмем 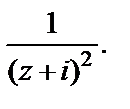 Тогда
Тогда
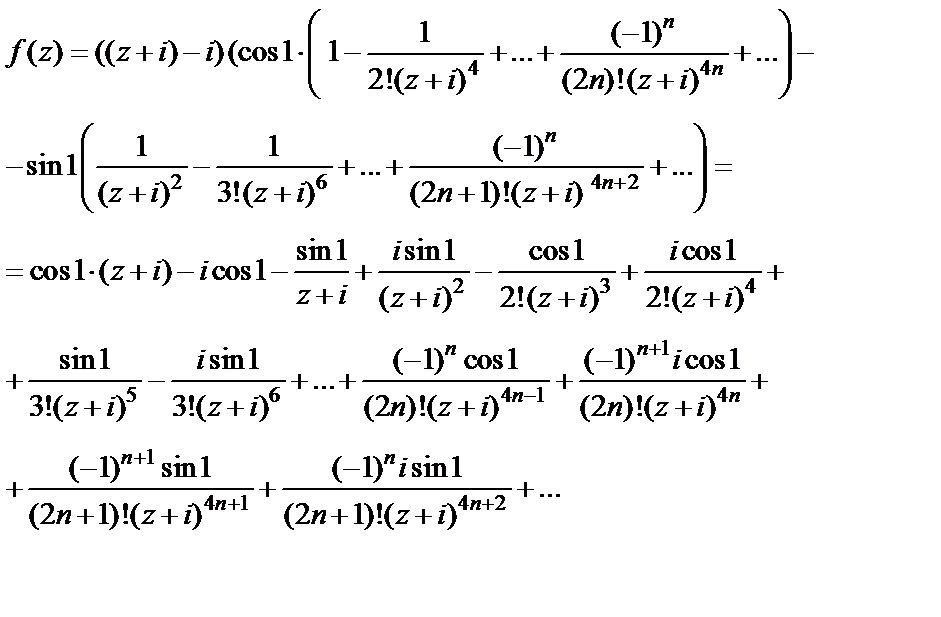
Видим, что полученный ряд Лорана данной функции содержит только два слагаемых правильной части и бесконечное множество слагаемых главной части.
Date: 2015-07-24; view: 763; Нарушение авторских прав