Нули и особые точки функции

Нулем аналитической в области D функции f(z) называется комплексное число 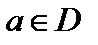такое, что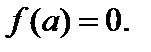

Если 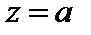есть нуль функции f (z), то 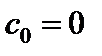в разложении функции f (z) в ряд Тейлора.

Точка a называется нулем кратности k (порядка k)функции f(z), если в разложении

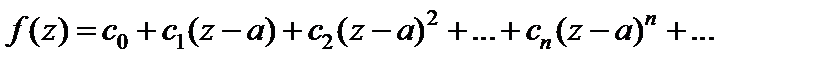(29.34)

выполняется 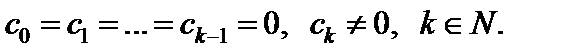При 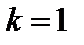нуль функции называют простым нулем.

В случае нуля кратности k разложение имеет вид:

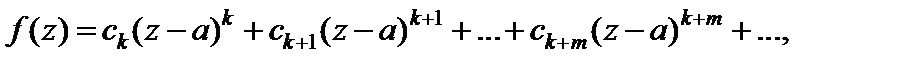
т. е. 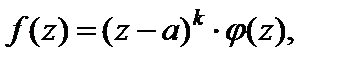(29.35)

где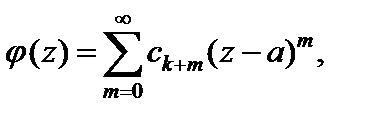

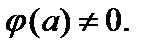
Заметим, что точка 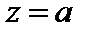является нулем кратности k, если

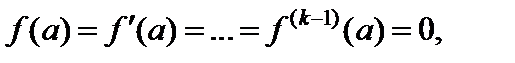
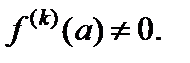(29.36)

Точка 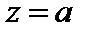называется изолированным нулемфункции f(z), 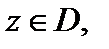если в области D существует окрестность с центром в точке a, которая не содержит других нулей этой функции.

Справедливо утверждение: нули аналитической в области D функции f (z) изолированы, если 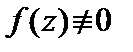на множестве D.

Точка 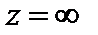называется нулем кратности k функции f (z), если ее ряд Лорана, построенный в окрестности точки 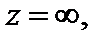не имеет главной части, а для коэффициентов правильной части выполняются условия

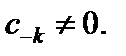(29.37)

При выполнении условий (29.37) ряд Лорана функции f (z) в окрестности точки 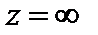имеет вид:

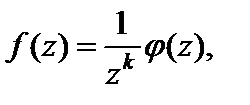(29.38)

где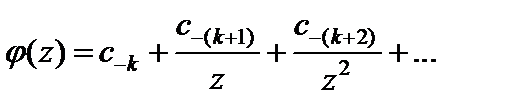

Точка 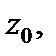в которой функция f (z) является аналитической, называется правильной точкой функции. Если функция f (z) аналитична в некоторой проколотой окрестности точки 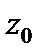и не аналитична в самой точке 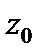(или не определена в ней), то 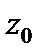называется изолированной особой точкой функции f (z).

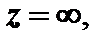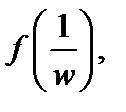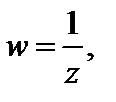
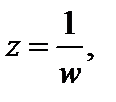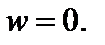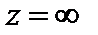Будем говорить, что функция f (z) является аналитической в бесконечно удаленной точке если функция где является аналитической в точке Точка называется особой точкой функции f (z), если точка 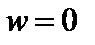является особой для функции 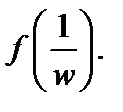Особая точка 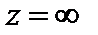является изолированной, если существует окрестность 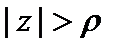такая, которая не содержит других особых точек функции f (z) (кроме ).

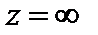Если выполняются условия:

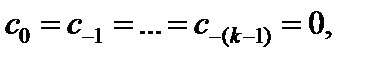
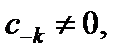
ряд Лорана функции f (z) в окрестности точки 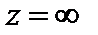имеет вид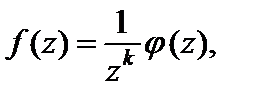

где 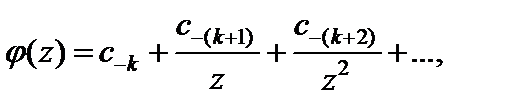причем

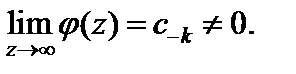
Особая точка a (изолированная особая точка) функции f (z) называется устранимой, если ряд Лорана (29.32) этой функции в проколотой окрестности точки a не содержит главной части.

Особая точка a функции f (z) является устранимой тогда и только тогда, когда f (z) ограничена в проколотой окрестности точки a.

Можно дать и такое определение устранимой особой точки: точка a называется устранимой особой точкой функции f (z), если существует конечный предел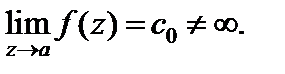

Особая точка a функции f (z) называется полюсом, если ряд Лорана этой функции в проколотой окрестности точки a содержит конечное число элементов главной части, т. е. имеет вид

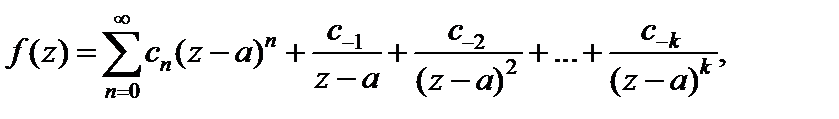
где 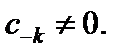При этом точка a называется полюсом k-го поряд­ка 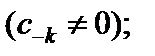при 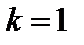полюс еще называют простым полюсом.

Особая точка a функции f (z) является полюсом тогда и только тогда, когда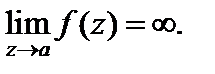

Справедливо утверждение: если точка a является полюсом k - го порядка функции f (z) (или нулем кратности k), то для функции 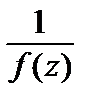точка a является нулем кратности k (соответственно полюсом порядка k).

Если функция f (z) имеет вид

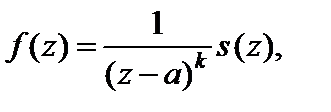(29.39)

где s (z) – аналитическая функция и 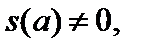то точка 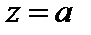есть полюс порядка k функции f (z).

Точка a называется существенно особой точкой функции f (z), если ряд Лорана этой функции в проколотой окрестности точки a содержит бесконечное количество ненулевых элементов главной части. Можно дать и такое определение: точка a называется существенно особой точкой функции f (z), если 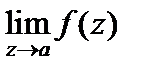не существует.

Пусть функция f (z) разложена в ряд Лорана в окрестности точки 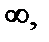т. е.

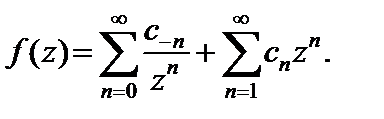(29.40)

Бесконечно удаленная точка 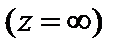называется:

1) устранимой особой точкой функции f (z), если ее разложение (29.40) в ряд Лорана не содержит положительных степеней z;

2) полюсом порядка k, если разложение содержит конечное число элементов с положительными степенями z, причем последним ненулевым коэффициентом является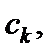

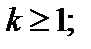
3) существенно особой точкой, если это разложение содержит бесконечное число положительных степеней z.

Пример 1. Найти нули функции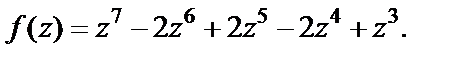

Решение. Данная функция является многочленом седьмой степени. Нули этой функции являются корнями многочлена. Поскольку

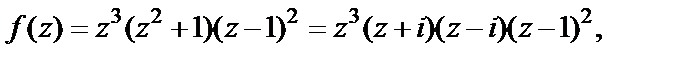
то 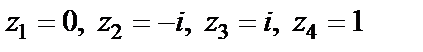– нули данной функции.

Других нулей нет, так как нет других корней многочлена.

Пример 2. Определить порядок нуля 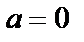функции:

1) 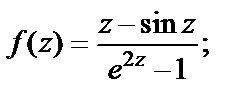2)

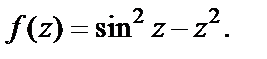
Решение. 1) Используем разложения функци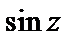й и 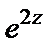в ряд Маклорена. Согласно формулам (29.29), получаем

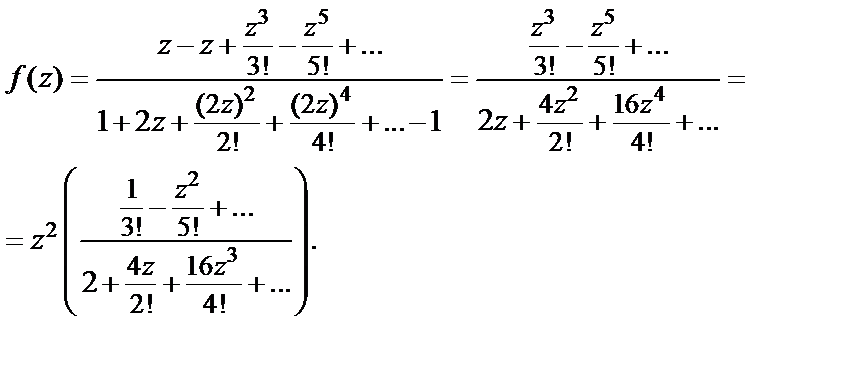
Поскольку при 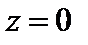функция, которая стоит в скобках, не равна нулю, то, согласно равенству (29.35), значение 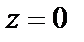есть нуль кратности два.

2) Используем другой способ исследования кратности нуля – проверим выполнение условий (29.36) в точке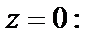

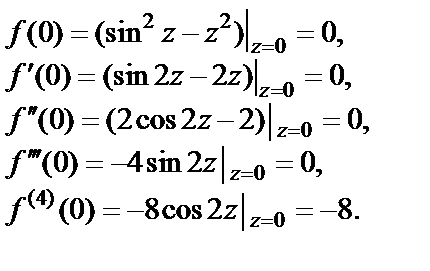
Учитывая то, что

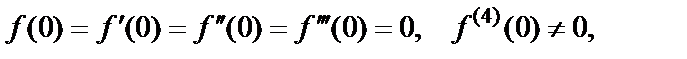
приходим к заключению, что есть нуль кратности четыре.

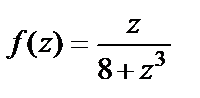Пример 3. Выяснить, является ли точка нулем функции и какой кратности (если это нуль).

Решение. Преобразуем выражение, которым определяется функция, к виду

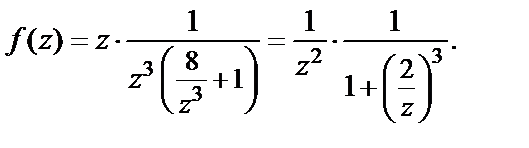
Для окрестности 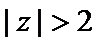бесконечно удаленной точки имеем 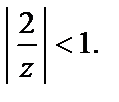Поэтому, используя формулу суммы геометрического ряда, получаем

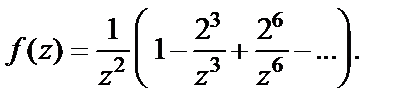
Сопоставляя полученное равенство с формулой (29.38), приходим к заключению, что 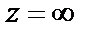есть нуль данной функции кратности два.

Пример 4. Найти особые точки функции и определить их тип:

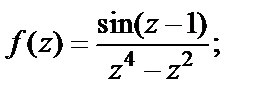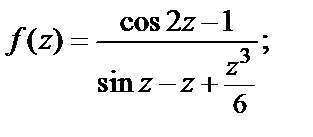1) 2) 3)

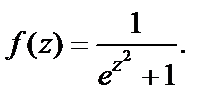
Решение. 1) Очевидно, что для 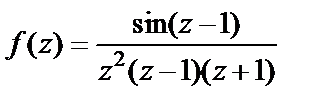особыми точками функции являются нули знаменателя. Поскольку числитель не равен нулю пр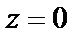и и 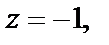то значения 0, – 1 есть соответственно полюс кратности два и простой полюс. Точку 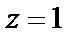надо исследовать отдельно. Для этого вычислим следующий предел:

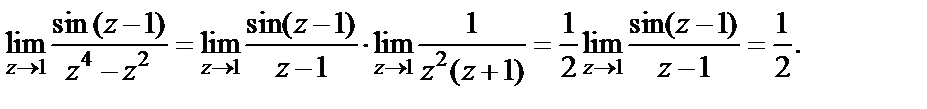
(убедиться в том, что последний предел равнен 1, можно, например, разложив 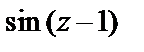в ряд Тейлора по степеням (z – 1)). Получив предел 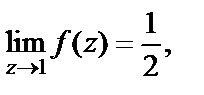приходим к заключению, что 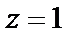– устранимая особая точка.

2) Видно, что особой точкой функции является точка 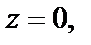в которой знаменатель принимает нулевое значение. Однако числитель дроби тоже равен нулю для 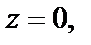а поэтому сразу определить тип особой точки мы не можем. Для его определения разложим функци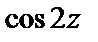и и 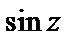в ряд Маклорена. Получим

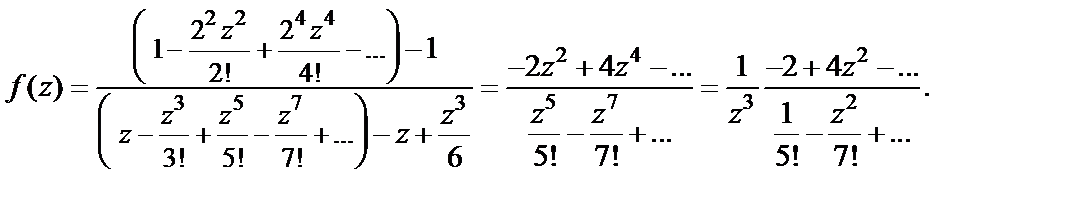
Поскольку степенные ряды, которые стоят в числителе и знаменателе последней дроби, представляют аналитические и отличные от нуля функции в окрестности точки 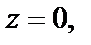то данная функция может быть записана в виде

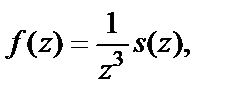
где s (z) – аналитическая функция, 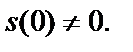В соответствии с формулой (29.39) приходим к заключению, что точка 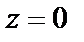есть полюс 3-го порядка.

3) Рассмотрим функцию 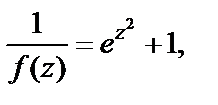которая является знаменателем данной дроби. Найдем ее нули:

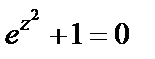– то самое, что 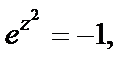т. е. 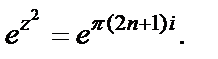Поэтому нули этой функции есть 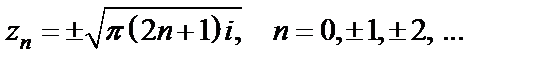Определим кратность полученных нулей. Поскольку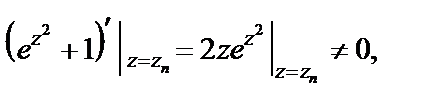 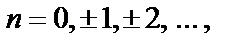то все точки z_n – простые нули. Тогда для данной функции эти точки есть простые полюсы, причем их бесконечно много (на координатной плоскости они размещаются на двух биссектрисах координатных углов).

Пример 5. Найти особые точки функции 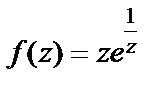и выяснить их тип.

Решение. Очевидно, что функция определена и дифференцируема на всей комплексной плоскости, кроме точки 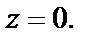Выясним тип особой точки, разложив данную функцию в ряд Лорана в окрестности этой точки. Для этого воспользуемся формулой (29.29) для представления экспоненты рядом Маклорена. Получим

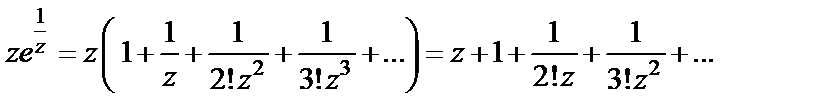
Ряд содержит бесконечное количество слагаемых в главной части, т. е. 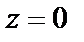– существенно особая точка функции.

Date: 2015-07-24; view: 2685; Нарушение авторских прав