
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства функций, непрерывных в точке и на множестве
|
|
1. Если f (z) и g (z) – непрерывные функции в точке 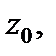 то непрерывными в этой точке являются также функции:
то непрерывными в этой точке являются также функции:
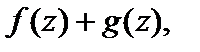
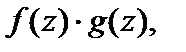
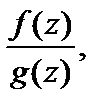
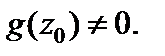
2. Пусть 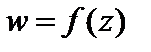 есть непрерывная функция на множестве D и она имеет множество значений G, на котором определена непрерывная функция g (w). Тогда сложная функция
есть непрерывная функция на множестве D и она имеет множество значений G, на котором определена непрерывная функция g (w). Тогда сложная функция 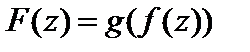 есть непрерывная функция на множестве D.
есть непрерывная функция на множестве D.
3. Пусть множество D является ограниченным и замкнутым, а функция f (z) – непрерывной на D. Тогда f (z) является функцией, ограниченной на множестве D, т. е. 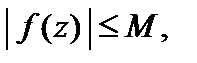
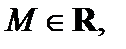 и ее модуль достигает на этом множестве своих точных нижней и верхней граней.
и ее модуль достигает на этом множестве своих точных нижней и верхней граней.
Пример 1. Найти действительную и мнимую части функции 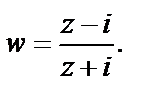
Решение. В формулу, которая задает функцию, вместо w подставим 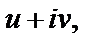 а вместо z –
а вместо z –  и получим:
и получим:
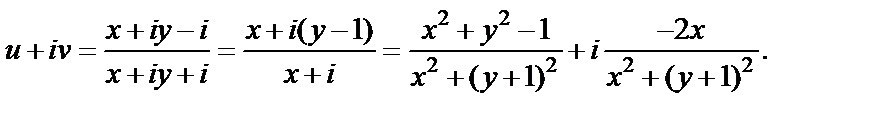
В результате находим
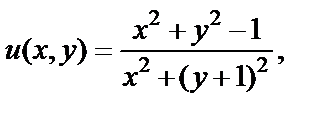
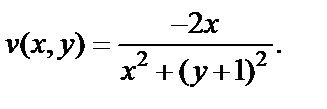
Пример 2. Выразить функцию  в виде зависимости от аргумента z, где
в виде зависимости от аргумента z, где 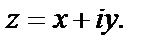
Решение. Функция w записана в виде 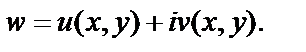 Очевидно, что
Очевидно, что
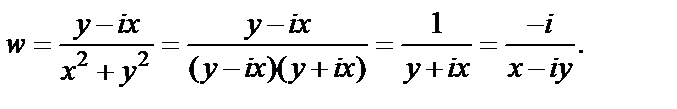
Используя понятие сопряженного комплексного числа, приходим к ответу 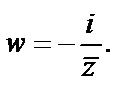
Пример 3. Дано отображение 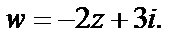 Найти образ линии:
Найти образ линии:
1) 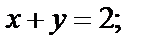 2)
2) 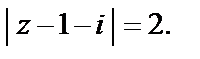
Решение. 1) Выделим действительную и мнимую части функции 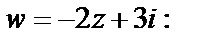
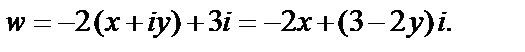
Для прямой 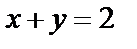 рассмотрим систему уравнений
рассмотрим систему уравнений
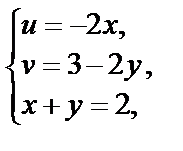
из которой находим 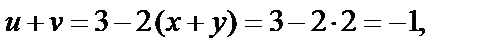 т. е.
т. е. 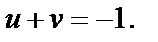
Значит, образом прямой 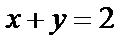 является прямая
является прямая 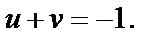
2) Для заданной окружности рассмотрим систему уравнений:
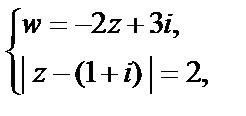 из которой получаем
из которой получаем 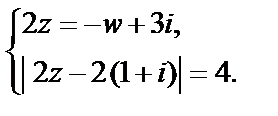
Тогда 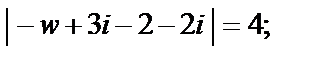
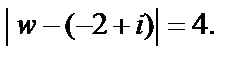
Следовательно, образом заданной окружности радиуса 2 с центром в точке 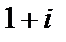 является окружность радиуса 4 с центром в точке
является окружность радиуса 4 с центром в точке 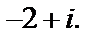
Пример 4. Найти образ прямой 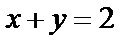 при отображении
при отображении 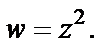
Решение. Выделим действительную и мнимую части функции 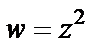 и решим полученную систему уравнений для прямой
и решим полученную систему уравнений для прямой 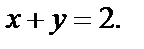 Тогда
Тогда
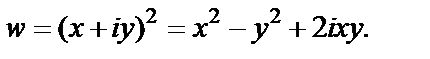
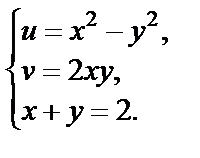
Находим:
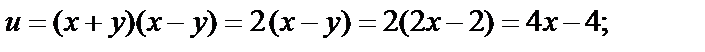
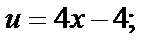
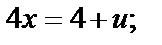
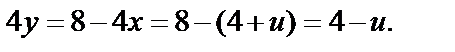
Тогда
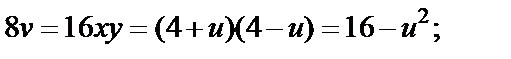
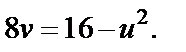
Таким образом, прямая 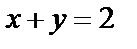 при отображении
при отображении  переходит в параболу
переходит в параболу 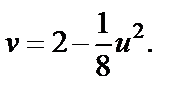
Пример 5. Найти образ множества точек, ограниченных прямыми 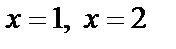 (образ полосы), при отображении
(образ полосы), при отображении 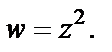
Решение. Изобразим заданную полосу (рис. 29.1, а). Выясним, на какую линию отображается функцией 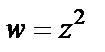 граница
граница  Параметрические уравнения этой прямой
Параметрические уравнения этой прямой
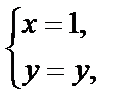 где
где 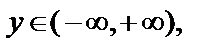 y – параметр. Тогда в комплексном виде линия задается уравнением
y – параметр. Тогда в комплексном виде линия задается уравнением 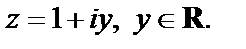 Поскольку
Поскольку 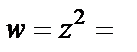
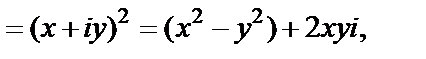 то, используя параметрические уравнения заданной прямой линии, имеем
то, используя параметрические уравнения заданной прямой линии, имеем 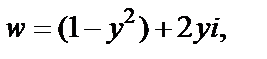 т. е.
т. е.
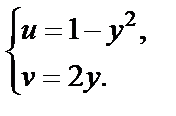
| х |
| у |
| Сz |
| х |
| у |
| Сw |
| а) б) |
Рис. 29.1
Из последней системы получаем 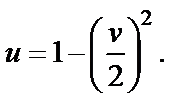 Таким образом, приходим к уравнению параболы
Таким образом, приходим к уравнению параболы 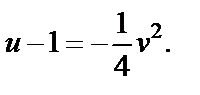 Аналогично можно убедиться в том, что прямая
Аналогично можно убедиться в том, что прямая  отображается функцией
отображается функцией 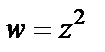 на параболу
на параболу 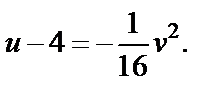 Если взять произвольную прямую
Если взять произвольную прямую 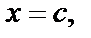
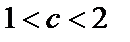 (которая параллельна границам и лежит внутри полосы), то ее образ при отображении
(которая параллельна границам и лежит внутри полосы), то ее образ при отображении 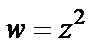 есть парабола
есть парабола 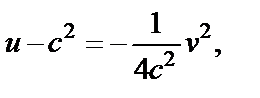 которая лежит между параболами
которая лежит между параболами 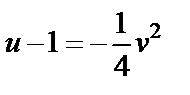 и
и 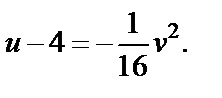
Значит, полоса с плоскости 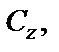 ограниченная прямыми
ограниченная прямыми 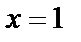 и
и 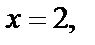 отображается на полосу, ограниченную названными параболами в плоскости
отображается на полосу, ограниченную названными параболами в плоскости 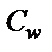 (рис. 29.1, б).
(рис. 29.1, б).
Пример 6. Выяснить, имеет ли функция 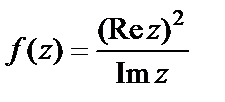 предел в точке
предел в точке 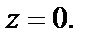
Решение. Для ответа на поставленный вопрос воспользуемся определением предела по Гейне. Рассмотрим сначала последовательность точек 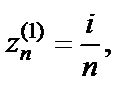
 Очевидно, что
Очевидно, что 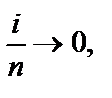 если
если 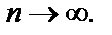 Поскольку
Поскольку 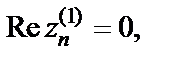 то
то 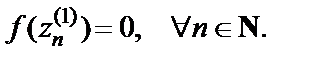 Значит,
Значит, 
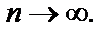
Возьмем теперь последовательность точек 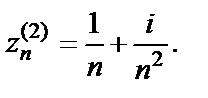 Для нее тоже выполняется
Для нее тоже выполняется 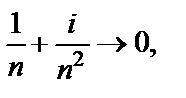 если
если 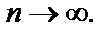 Однако
Однако 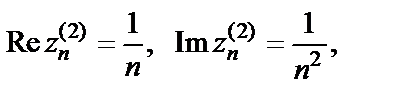 а поэтому
а поэтому 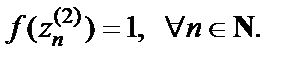 Значит,
Значит, 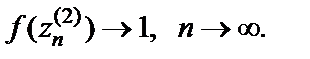
Мы получили, что для двух последовательностей аргументов 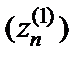 и
и 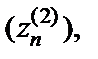 таких, что
таких, что 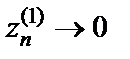 и
и 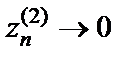 при
при 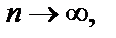 последовательности соответствующих значений функции сходятся к разным числам. Поэтому заданная функция не имеет предела в точке
последовательности соответствующих значений функции сходятся к разным числам. Поэтому заданная функция не имеет предела в точке 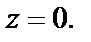
Пример 7. Вычислить предел функции:
1) 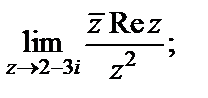 2)
2)  3)
3) 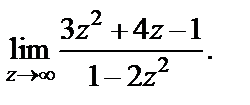
Решение. 1) Перейдем к функции двух переменных под знаком предела. Тогда
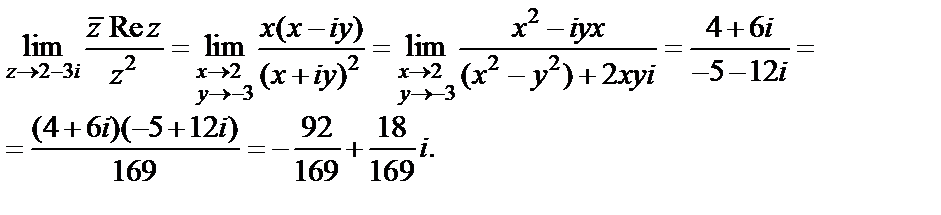
2) Непосредственный переход к частному пределов приводит к неопределенности типа 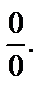 Поэтому сначала преобразуем выражение, стоящее под знаком предела, а затем вычислим предел:
Поэтому сначала преобразуем выражение, стоящее под знаком предела, а затем вычислим предел:
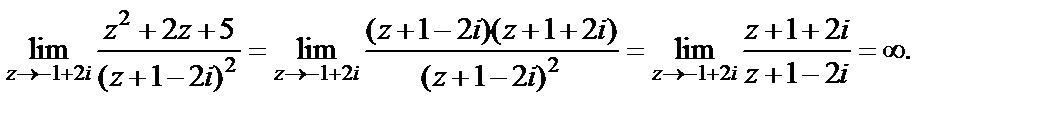
3) После деления на старшую степень числителя и знаменателя дроби (как это делается для действительных функций) получим
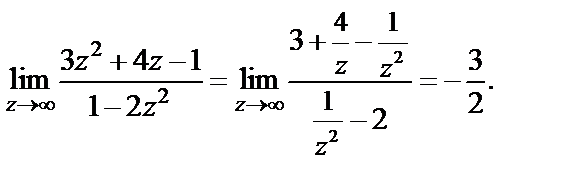
Пример 8. Найти предел 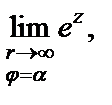 если:
если:
1) 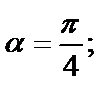 2)
2)  3)
3) 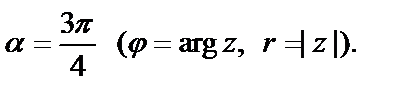
Решение. Заметим, что 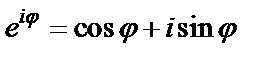 и, значит,
и, значит,

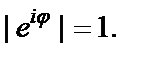
1) Рассмотрим 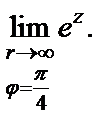
Имеем 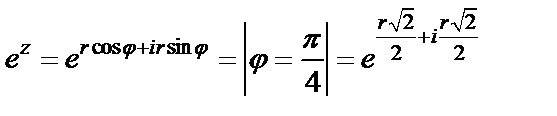
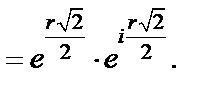 Тогда
Тогда
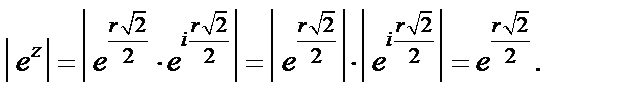
Так как 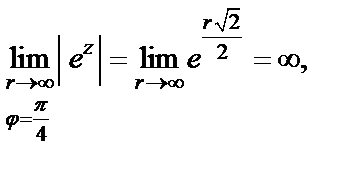 то
то 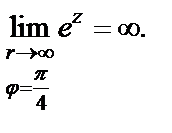
2) В этом случае 
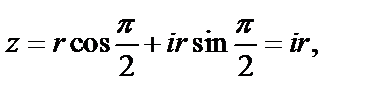
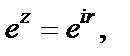
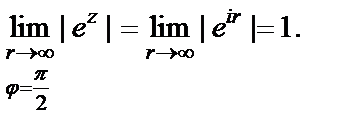
Покажем, что, несмотря на существование предела 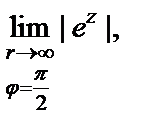 не существует предел
не существует предел 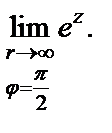
Запишем
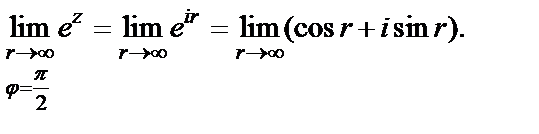
Используем определение предела по Гейне. Сначала рассмотрим последовательность 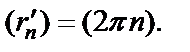
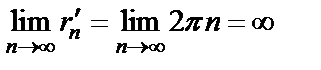
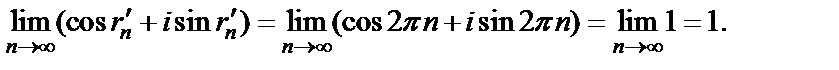
Затем рассмотрим последовательность 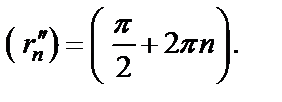
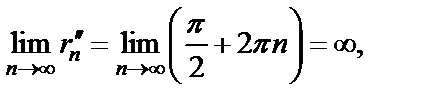
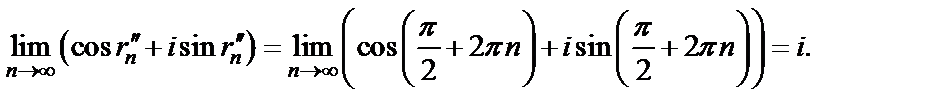
Таким образом, указаны две последовательности 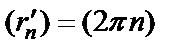 и
и 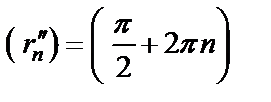 такие, что
такие, что
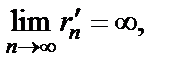
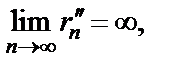 но
но 
Значит, 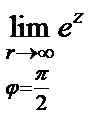 не существует.
не существует.
3) При 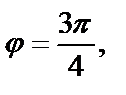 имеем
имеем
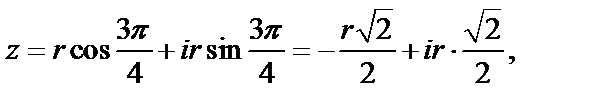
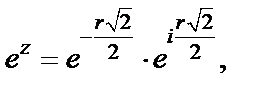
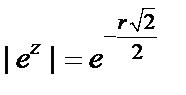 и
и
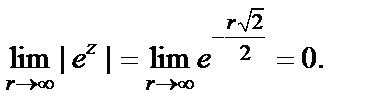
Отсюда следует, что 
Пример 9. Исследовать на непрерывность функцию:
1) 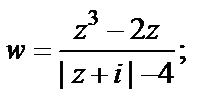 2)
2) 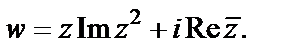
Решение. 1) Очевидно, что функция определена на всей плоскости Ĉ. Непрерывной она является во всех ее точках, кроме тех, где знаменатель равен нулю, т. е. 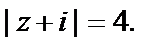 Иначе говоря, множество точек разрыва функции лежит на окружности радиуса
Иначе говоря, множество точек разрыва функции лежит на окружности радиуса 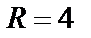 с центром в точке
с центром в точке 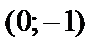 (в этих точках функция принимает значение
(в этих точках функция принимает значение 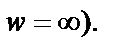
2) Для исследования данной функции на непрерывность отделим ее действительную и мнимую части:
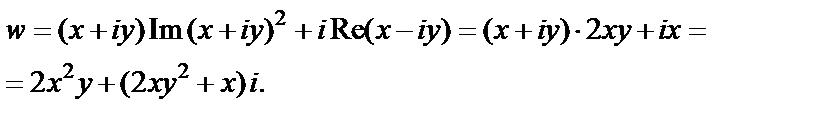
Обе функции 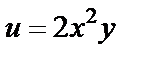 и
и 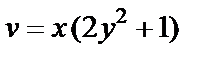 являются непрерывными для всех
являются непрерывными для всех 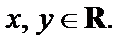 Значит, данная функция непрерывна на всей плоскости C.
Значит, данная функция непрерывна на всей плоскости C.
Пример 10. Доказать, что функция 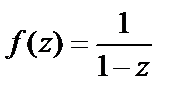 является непрерывной внутри единичного круга
является непрерывной внутри единичного круга 
Решение. Пусть 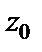 – произвольная точка, лежащая внутри круга
– произвольная точка, лежащая внутри круга 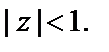 Обозначим
Обозначим 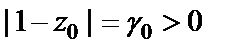 и заметим, что для всех z, удовлетворяющих условию
и заметим, что для всех z, удовлетворяющих условию  выполняется неравенство
выполняется неравенство 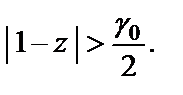
Преобразуем разность 
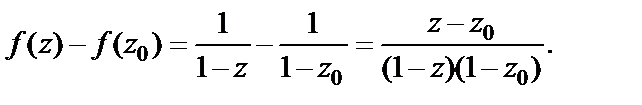
Возьмем произвольное 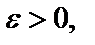 обозначим
обозначим 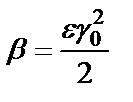 и положим
и положим 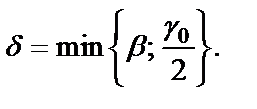 Тогда для любого z, такого, что
Тогда для любого z, такого, что  будет
будет
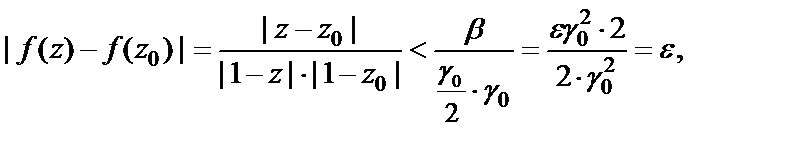
т. е. 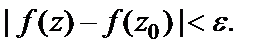
Непрерывность функции в точке 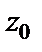 доказана, а поскольку
доказана, а поскольку 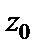 – произвольная точка круга
– произвольная точка круга 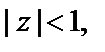 то доказана непрерывность f (z) внутри круга
то доказана непрерывность f (z) внутри круга 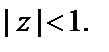
Пример 11. Записать уравнение линии в комплексной форме:
1) 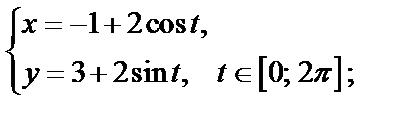 2)
2) 
Решение. 1) Это параметрические уравнения окружности радиусом, равным 2, с центром 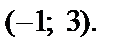 Поскольку
Поскольку 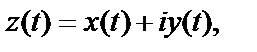 то уравнение данной линии можно записать в виде
то уравнение данной линии можно записать в виде
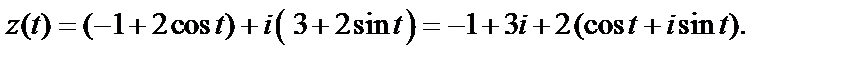
Воспользуемся формулами Эйлера:
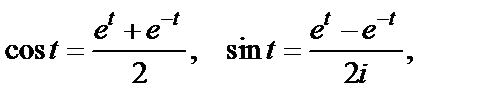 откуда
откуда
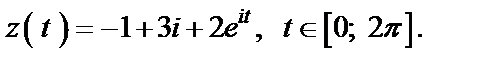
Из последней записи видно, какой центр имеет окружность и каков ее радиус.
2) Если обе части заданного уравнения поделить почленно на 36, придем к уравнению эллипса
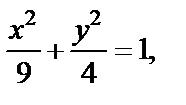
который имеет центр в точке (0; 0). Его параметрические уравнения:
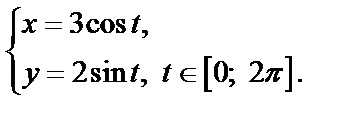
Значит, в комплексной форме это уравнение принимает вид
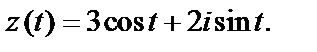
Пример 12. Определить, какую линию на плоскости задает уравнение:
1) 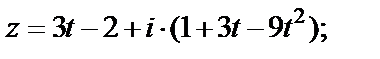 2)
2) 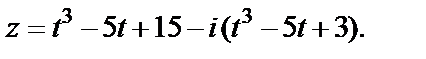
Решение. 1) Сначала запишем уравнение линии в параметрическом виде:
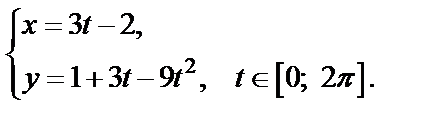
Из первого равенства выразим t через x и подставим в другое:
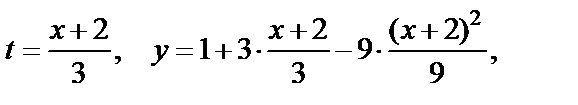 т. е.
т. е. 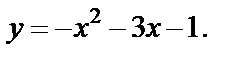 Как известно, это есть уравнение параболы.
Как известно, это есть уравнение параболы.
2) Переходим к параметрическому заданию линии:
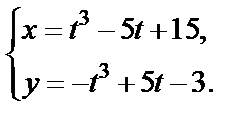
Сложив эти равенства, получим 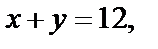 что есть уравнение прямой. (Для строгости рассуждений и в первом, и во втором случаях убедитесь в обратном: каждая точка параболы
что есть уравнение прямой. (Для строгости рассуждений и в первом, и во втором случаях убедитесь в обратном: каждая точка параболы  и каждая точка прямой
и каждая точка прямой 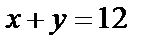 задается соответствующей системой с параметром).
задается соответствующей системой с параметром).
Date: 2015-07-24; view: 1178; Нарушение авторских прав