Свойства гиперболических функций

1. Функции 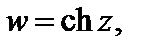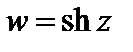определены и непрерывны на плоскости C.

2. Производные функций 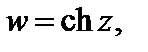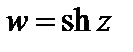существуют для любого 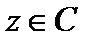и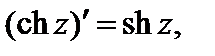

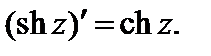
3. Справедливы равенства:

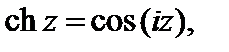
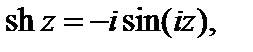
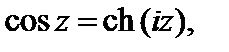
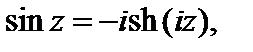(29.8)

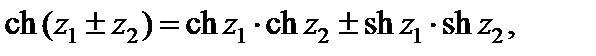
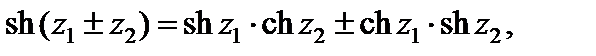
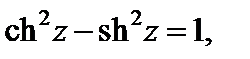
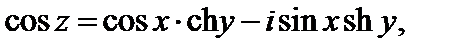
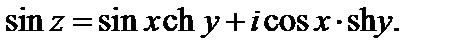
4. Функции th z и cth z определены и непрерывны всюду на плоскости C, кроме нулей знаменателей.

Пример 1. Доказать, что для функции 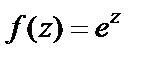справедлива формула

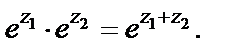(29.9)

Решение. Пусть 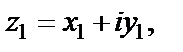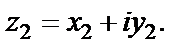Используя свойства степени и формулу Эйлера, получим:

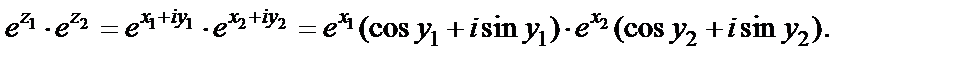
Далее, перемножая выражения в скобках и используя тригонометрические формулы для косинуса и синуса суммы двух аргументов, получаем:

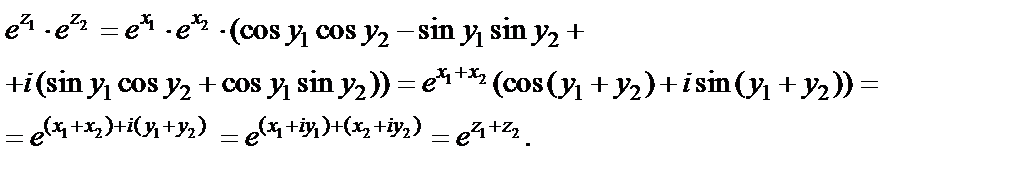
Равенство (29.9) доказано.

Пример 2. Доказать равенство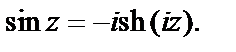

Решение. Используем определение гиперболического синуса. Тогда

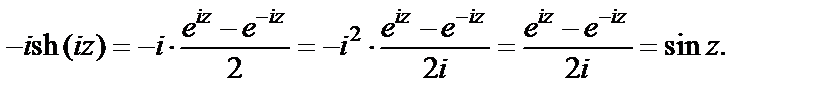
Заданное равенство доказано.

Пример 3. Доказать равенство

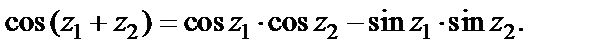(29.10)

Решение. Преобразуем правую часть заданного равенства, используя формулы (29.7):

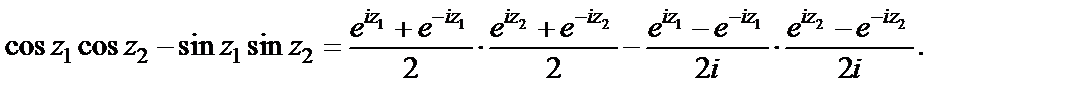
Выражения перемножаем и по формуле (29.7) получаем:

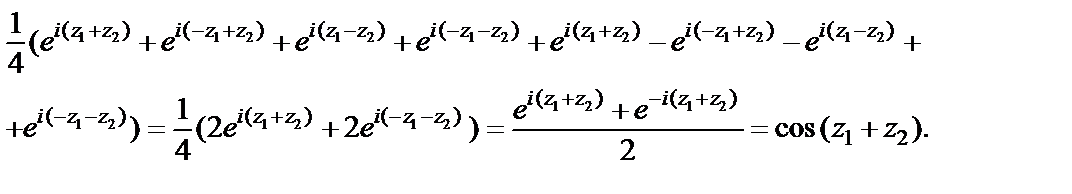
Равенство (29.10) доказано.

Пример 4. Найти действительную и мнимую части функции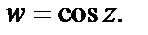

Решение. Так как 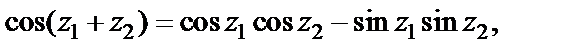то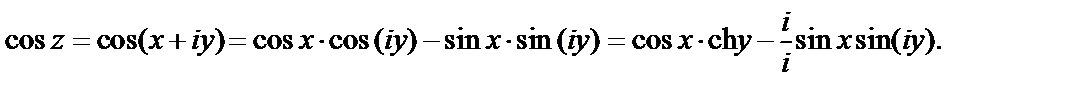

Используем далее формулу (29.8). Тогда

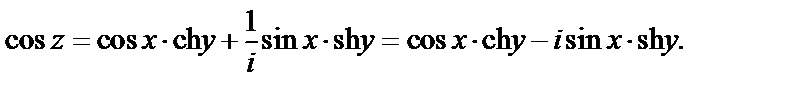
Значит, для 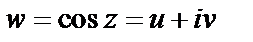будет

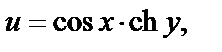
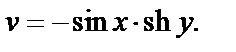
Пример 5. Выяснить, на какое множество точек плоскости 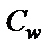функция 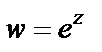отображает прямую линию с плоскости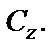

Решение. Рассмотрим три случая таких прямых.

1. Пусть z «пробегает» прямую, параллельную мнимой оси Oy: 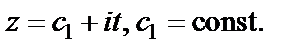Тогда 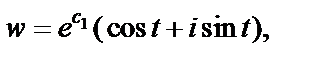т. е. образом такой прямой является окружность радиуса 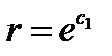с центром в начале системы координат Ouv. При этом, когда точка z «пробегает» рассматриваемую прямую один раз (координата t непрерывно меняется от 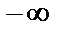до 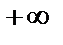), то образ w «пробежит» (в положительном направлении) соответствующую окружность бесконечное количество раз.

2. Пусть z «пробегает» прямую, параллельную действительной оси Ox: 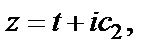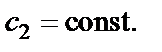Тогда 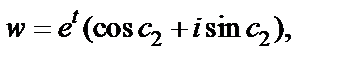т. е. множество образов лежит на луче, который выходит из начала системы координат и образует с осью Ou угол 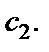При этом, когда точка z «пробегает» прямую один раз (абсцисса t непрерывно изменяется от 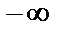до 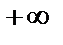), то образ w тоже один раз «пробегает» соответствующий луч (расстояние от начала системы координат до точки w непрерывно растет от 0 до ).

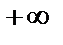3. Пусть z «пробегает» прямую, которая не параллельна координатным осям. Уравнение такой прямой имеет вид 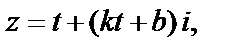где k – угловой коэффициент прямой; b – ордината при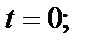 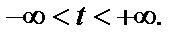Тогда образом такой прямой является кривая

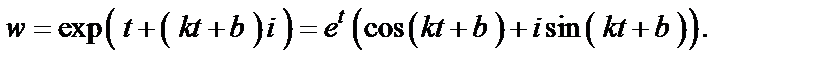
Для точки w, которая лежит на этой кривой (при условии, что 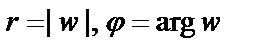), имеем: 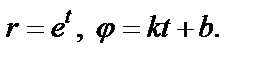Из второго равенства выразив t через и подставив в первое, получим 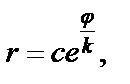где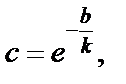

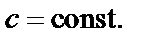
Это уравнение логарифмической спирали.

Пример 6. Выяснить, на какое множество точек функция

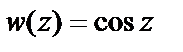отображает полуполосу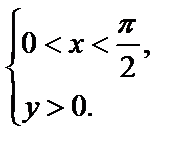

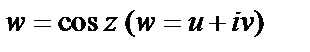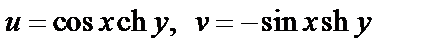
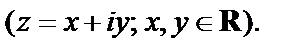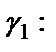
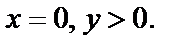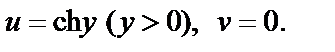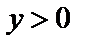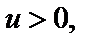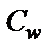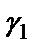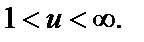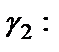
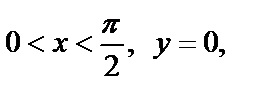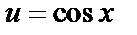
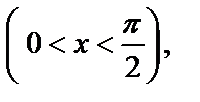
Решение. Обозначим данную в условии полуполосу через d. 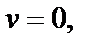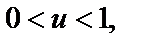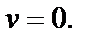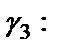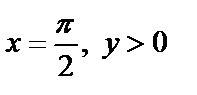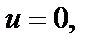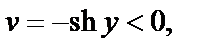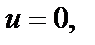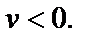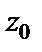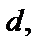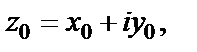Согласно восьмой формуле (29.8), для функции имеем Найдем сначала образ луча Очевидно, что он отображается на множество точек Поскольку для имеем то в плоскости образом луча будет луч Г₁ Аналогично определим, что интервал отображается на множество которое является интервалом Г₁: И наконец, луч преобразуется в множество которое является лучом Г₃: Выберем внутреннюю точку полосы 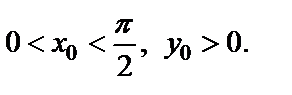Для этой точки получаем следующие значения: 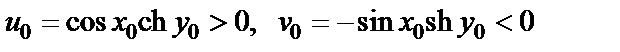– образ принадлежит четвертой координатной четверти. Это значит, что внутренние точки полосы d отображаются на внутренние точки множества D четвертой четверти, причем это взаимно-однозначное отображение.

Date: 2015-07-24; view: 567; Нарушение авторских прав