Изменение технического состояния механизмов в процессе эксплуатации. Кривая Вейбулла

Поскольку автомобиль является восста­навливаемой системой, определение тактики и стратегии восстанов­ления его работоспособности имеет большое значение. В связи с этим целесообразно рассмотреть процесс работоспособности объекта эксплуатации. Объектом эксплуатации могут быть сопряжения, агрегат, узел или автомобиль в целом. Работоспособность — это способность автомобиля выполнять необходимые функции, а также состояние эксплуатационных качеств в допустимых пределах.

Общая схема потери работоспособности объекта эксплуатации приведена на рис. где х — один из параметров, характеризую­щих его работоспособность. Таких параметров может быть несколь­ко. Параметр х может иметь любой физический смысл. На каждый параметр устанавливаются допустимые пределы, соответственно

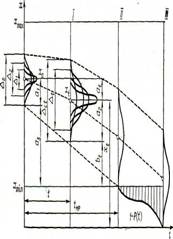
Схема потери работоспособности объекта эксплуатации

минимальные х_тin и максимальные х_тах значения параметра. Если параметр находится в интервале *_min.--*max, объект считается рабо­тоспособным. В том случае, когда хотя бы один из параметров вы­ходит за пределы допусков, объект теряет работоспособность.

Предположим, что в процессе эксплуатации объекта значение параметра х постепенно уменьшается. Тогда изменение параметра х от начального значения до х_тiп представляет собой процесс измене­ния технического состояния объекта, постоянную потерю им рабо­тоспособности.

В качестве примера рассмотрим потерю работоспособности дви­гателя. Мощность двигателя обозначим через х. При конструирова­нии и изготовлении двигателя различные его узлы и механизмы обладают геометрической неточностью из-за конструктивных осо­бенностей и степени несовершенства изготовления, что в эксплуа­тации приводит к разбросу значений х у двигателей выпускаемой заводом серии. Чаще всего разброс значений х подчиняется нор­мальному закону. Обозначим рассеивание буквой ∆₁.(рис)

У работающего двигателя в силу действия быстро протекающих физических процессов произойдет дальнейшее увеличение отклоне­ния, которое определится полем рассеивания ∆₂. Используя вероят­ностный метод сложения дисперсий отдельных процессов, получаем суммарное поле рассеивания:

∆_с =√∆²₂ + ∆²₂

Центр группирования начальных значений параметра обозна­чим через х₀. Тогда запас параметра

a₃ = x₀ – a₁ -x_min

где a_x = l/2∆_с — начальная неточность значения параметра.

В процессе эксплуатации двигателя происходит постепенное изнашивание его деталей. Это обстоятельство учитывается в модели тем, что предполагается наличие средней скорости v уменьшения центра группирования значений параметров. За время t начальное значение х₀ сместится на a_t = vt.

Поскольку процесс изнашивания происходит не детерминированно, а случайно, здесь также будет поле рассеивания, которое обозначим через ∆_t. К моменту t после начала эксплуатации сум­марное рассеивание значений параметра имеет вид

∆_сt =√ ∆²₁ + ∆²₂ +∆²_t,

а среднее отклонение значений параметра

а₂ = ½ ∆_ct.

В момент t центр группирования значений параметра x_t = х₀ — a_t, а остающийся резерв b_t доводят до минимально допус­тимого уровня:

b_t =x_t – a₂- x_min = x₀- a_t – a₂ -x_min

Рассматриваемому моменту на рис. соответствует состояние I.

В дальнейшем при эксплуатации двигателя возрастает возмож­ность выхода параметра х за минимально допустимый уровень. Количественно это можно оценить вероятностью безотказной ра­боты Р (t) за время t.

При нормальном законе рассеивания параметров вероятность безотказной работы Р (t) можно определить из выражения:

P_t= 0,5 + Ф(х_t - х_min / 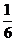∆_ct)

где 0 ≤ Ф ≥ 0,5 — нормированная функция Лапласа.

Вероятность безотказной работы Р (t) практически будет равна единице до тех пор, пока имеется резерв допустимых изменений параметра (т. е. b_t > 0). Опасность будут представлять лишь вне­запные отказы из-за внешних воздействий, не связанных с техни­ческим состоянием двигателя.

При длительной эксплуатации двигателя более интенсивно изнашиваются детали. В результате ухудшается его техническое состояние и в некоторый момент времени резерв исчерпывается (рис. состояние II). Вероятность отказа 1 — Р (t) будет быстро нарастать. Таким образом, момент исчерпания ресурса должен оп­ределять межремонтный ресурс изделия t_м._р.

Эксплуатация двигателей после момента времени t_м._р увеличи­вает зону рассеивания параметров и изменяет их техническое состо­яние. Это приводит к значительному уменьшению Р (t) (рис. Состояние III).

Для того чтобы управлять этим процессом, необходимо знать действительное техническое состояние автомобиля в любой момент времени. Решением всех вопросов и занимается техническая диаг­ностика. Она включает теорию и организацию процессов диагноза, а также принципы построения методов диагноза.

Date: 2015-07-23; view: 801; Нарушение авторских прав